코딩테스트 문제 유형 정리

Ilhwanee·2022년 5월 14일

코딩테스트

109

코딩테스트

목록 보기

1/155

코딩테스트에서 가장 중요한 것은 꾸준함이 아닐까...?

🔥 코딩테스트의 중요성

신입 개발자 채용의 경우 지원 후 코딩테스트로 일정이 시작되는 경우가 대부분이다.

물론 코딩테스트를 보지 않는 경우도 있겠지만, 선택의 폭이 많이 좁아질 것이다. (신입 기준)

또한 코딩테스트를 합격해야 서류전형이 시작되는 경우도 있고 코딩테스트에 합격해야 면접을 볼 수 있는 기회가 주어지기 때문에,

코딩테스트를 합격하는 것은 취업에 있어서 첫 단추를 끼우는 것과 같다.

👀 그렇다면 어떻게 준비해야 할까?

코딩테스트는 결국 많이 풀어본 사람이 유리하다.
주어진 시간동안 주어진 문제를 요구사항에 맞게 프로그래밍하는 것이기 때문이다.

즉, 문제의 요구사항에 맞게 풀이할 수 있는 자료구조, 알고리즘 등을 선택하여 활용할 수 있는 능력이 중요하다.

해당 유형을 많이 풀어봤으면 같은 유형의 문제를 풀이할 때 더 앞서갈 수 있다.

예) 프로그래머스 - 단어 변환
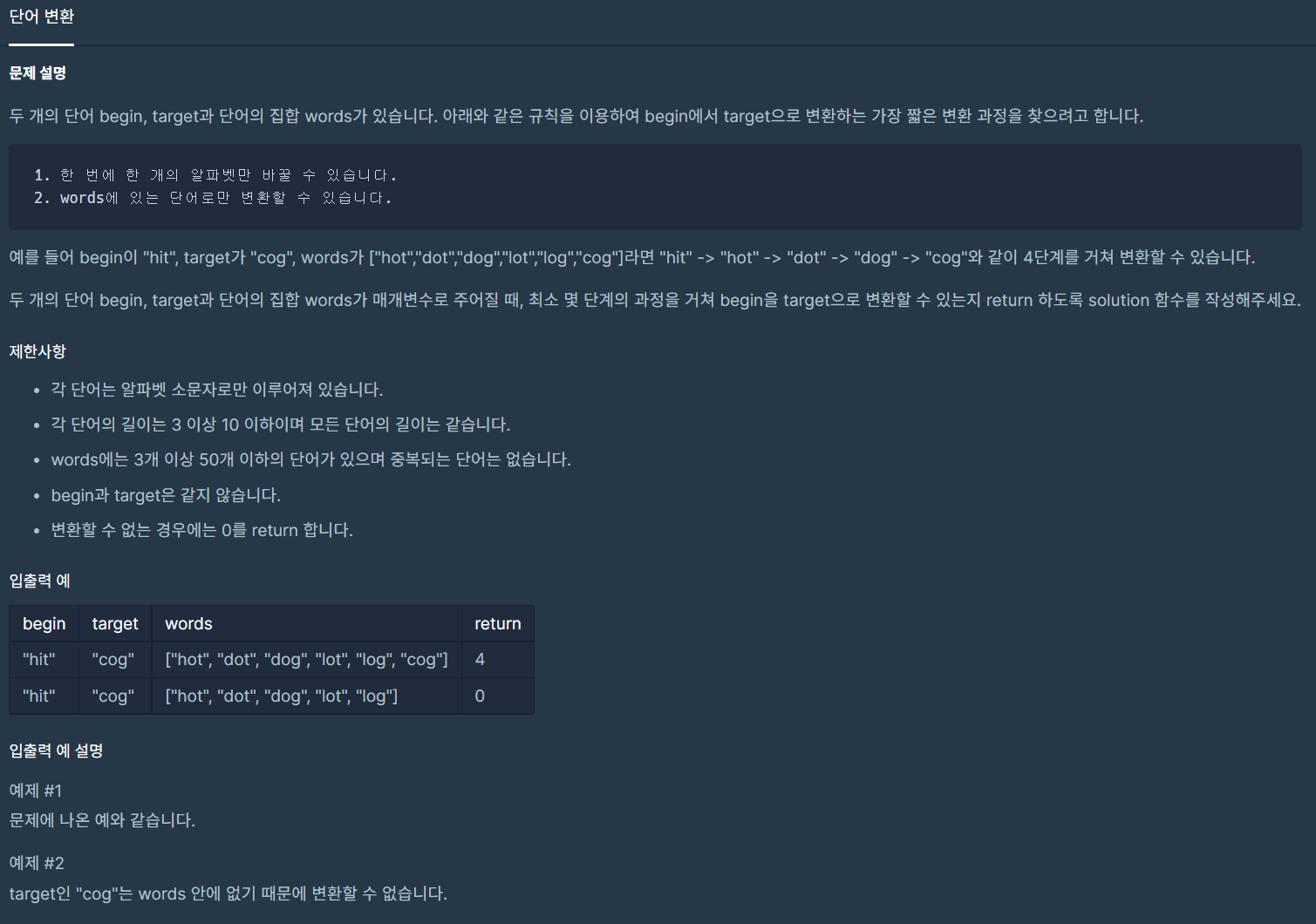
이와 같은 문제가 주어지는 경우 DFS/BFS 유형(완탐)의 문제들을 많이 풀어본 사람은 그렇지 않은 사람보다 빠르게 풀이 방법을 떠올릴 수 있다.
방문하지 않은 단어 중에 현재 단어에서 한 알파벳만 변경하여 변환 가능한 단어들로 DFS를 진행하고 목표에 도달한 경우 최소 변환 횟수를 갱신한다. 라는 결론에 빠르게 도달하여 이미 구현해본 DFS로 빠르고 정확하게 풀이할 수 있다.

🤔 그럼 모든 유형을 많이 풀어보면 되겠네?

모든 유형들을 충분히 준비 해놓을 수 있다면 그보다 더 좋은 것은 없을 것이다.

하지만 우리에겐 시간이라는 자원이 한정되어 있고 CS, 언어, 프레임워크, 프로젝트, 자소서, 포트폴리오, 면접 준비 등 준비해야할 것들이 너무나도 많다...

따라서 자주 기출되는, 내가 부족한 유형별로 우선순위를 정하여 준비해보자!

필자가 느끼기에 가장 자주 기출되는 유형은 구현, 완탐, DP이다.

✏️ 코딩테스트 문제 유형 정리

코딩테스트에는 시간 제한(효율성)이 존재하기 때문에 시간복잡도가 매우 중요하다.
만약 문제에서 주어진 N이 10,000 이라면 O(N^3) 풀이 방법으로는 시간 초과가 날 것이다. (대부분의 테스트 환경에서)

반대로 생각하면, 이것은 문제의 힌트와 같다! 시간복잡도를 고려하여 제한 시간내 성공 가능한 알고리즘이 문제의 정답이기 때문이다.
따라서 자료구조, 알고리즘의 시간복잡도는 반드시 알아야 한다.

✨ 해시 테이블

key-value 쌍으로 저장되는 특성에 따라 자주 사용된다.
유형이라기보다는 자주 사용되는 자료구조 정도가 맞는 것 같다.
예) 2020 KAKAO BLIND RECRUITMENT - 주차 요금 계산
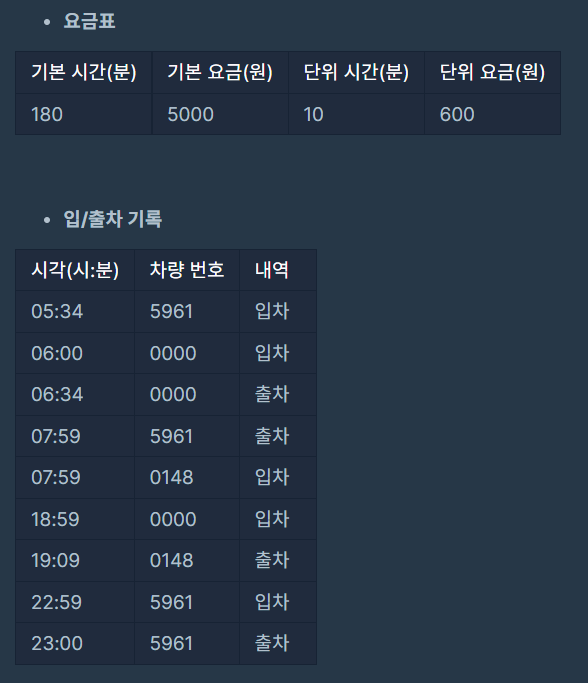
차량 번호를 key로, 입차 시간을 value로 저장한 뒤 출차할 때 해시 테이블에서 꺼내 계산

✨ 스택 & 큐

많이 사용되긴 하지만 단독으로 사용되는 경우보다 구현하는데 필요한 자료구조 정도로 사용되는 경우가 많다. 예) 스택 : DFS, 큐 : BFS
문제에서 선입선출, 후입선출의 단서가 보이면 사용하자!
예) 프로그래머스 - 다리를 지나는 트럭
다리는 먼저 들어간 차량이 먼저 나옴 -> 선입선출 -> 큐
반목문을 돌면서 다리가 버티는 무게를 계산하여 큐에 넣어주고 다 건넜으면 빼줌

✨ 힙

우선순위를 고려하는 문제에서 사용된다. 예) 작은 수부터, 큰 수부터
보통 Java의 경우 PriorityQueue로 사용한다. (그렇다고 힙 == PQ는 아님)
PriorityQueue의 경우 개선된 다익스트라의 구현에 사용된다.
예) 프로그래머스 - 더 맵게
스코빌 지수가 K이상이 될 때까지 반복문을 돌며 우선순위 큐에서 2개를 빼고 섞은 뒤 다시 넣음

✨ 구현

주어진 문제를 알고리즘을 통하여 코드로 바꾸는 것이다.
머리로 구상한 과정을 코드로 옮기는 능력이 중요하다.
주로 어렵지는 않지만, 복잡한 구현이 나올 때가 많다.
문제를 많이 풀어보는 것이 실력 향상에 도움이 되는 것 같다.
2020 KAKAO BLIND RECRUITMENT - 기둥과 보 설치 문제를 풀이해보길 추천한다.

✨브루트 포스(완전탐색)

코딩테스트 필수 of 필수일 만큼 자주 출제되는 유형으로 완탐이라고 줄여 부르기도 한다.
DFS, BFS, 백트래킹(완탐은 아니긴 하다)을 공부하자.
이름 그대로 모든 경우를 탐색해야 할 경우에 사용된다. (미로찾기 등)
무작정 모든 경우를 탐색하면 효율이 낮으므로, 시간 제한에서 실패하면 다른 풀이를 생각해보거나 문제 조건에 따라 탐색을 최소한으로 만들어야 한다.
예) 2020 KAKAO BLIND RECRUITMENT - 양궁대회
라이언이 쏠 수 있는 모든 경우의 수를 구하기 위해 DFS 사용하면 시간 초과가 뜸
어피치가 쏜 과녁 횟수의 + 1 이상이어야 라이언이 득점하므로 이 조건을 DFS에 추가하면 성공

✨ 다이나믹 프로그래밍

복잡한 문제를 한 번에 해결하는 것이 아닌, 조금씩 점차적으로 풀이하는 유형이다. (점화식을 떠올리면 이해하기 쉬움)
개인적으로 어려운 유형이라고 생각한다.
다른 유형도 그렇겠지만, 특히 DP는 여러 문제를 풀어보면서 감을 익혀보자.
bottom-up, top-down 을 모두 공부하자. (필자는 bottom-up 접근이 편하다고 생각)
한 문제를 bottom-up, top-down 두 방법으로 각각 풀이해보는 것도 좋다.
예) 프로그래머스 - 정수 삼각형
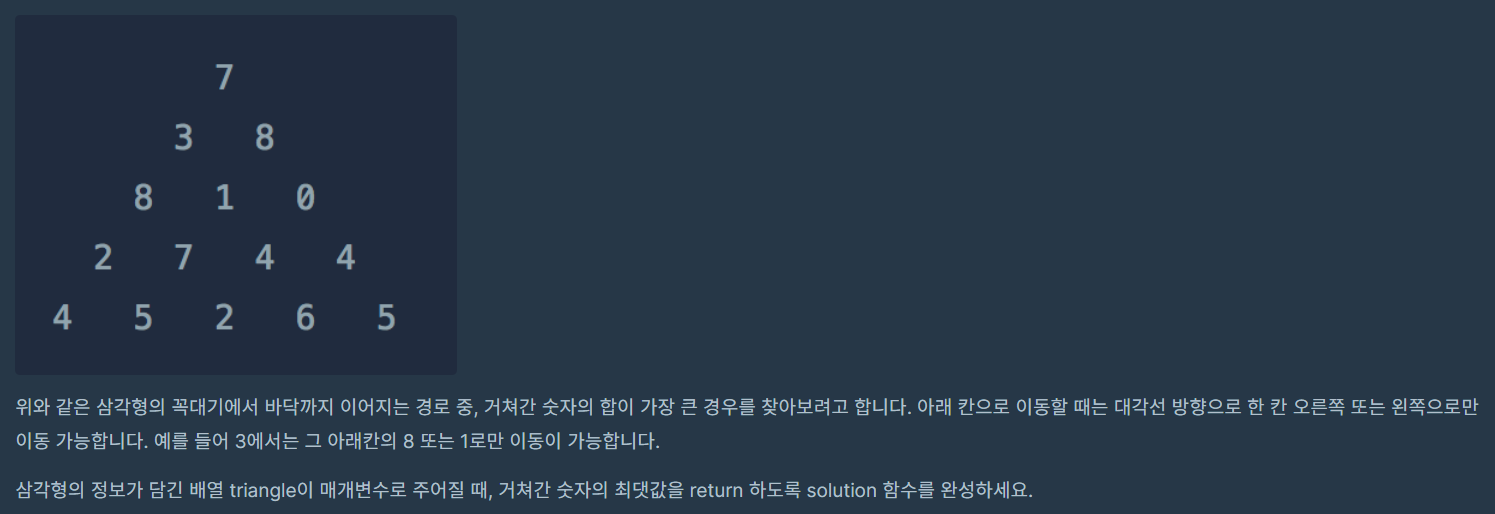
산보다 나무를 본다는 마음으로 가장 작은 삼각형 부터 시작
가장 위부터 0번째 인덱스라고 하면 1번째 인덱스의 solution은 10, 15
마찬가지로 2번째 인덱스의 solution은 18, 16, 15
그 다음으로 3번째 인덱스는... 반복하다보면 점화식이 보임

✨ 그리디

부분적인 최적해가 전체적인 최적해가 되는 문제에서 사용한다.
어렵게 출제되면 풀이를 쉽게 떠올리기 힘드니, 문제를 많이 풀어보면서 풀이 방법을 기억하자.
정렬, 우선순위 큐를 활용하는 경우가 많다.
예) 프로그래머스 - 큰 수 만들기
숫자가 증가할 때 까지 제거하다 숫자가 내려가면 가장 큰 수 keep 을 k 개 제거할 때 까지 반복

✨ 이분 탐색

순차적인 배열 탐색으로는 시간 초과가 나는 문제에서 사용한다.
시간 복잡도 : O(logN)로 그냥 순회하는 O(N)보다 빠르다.
이분 탐색 + 다익스트라 등 다른 유형과 연계되는 문제가 출제될 수 있다.
예) 2019 카카오 개발자 겨울 인턴십 - 징검다리 건너기
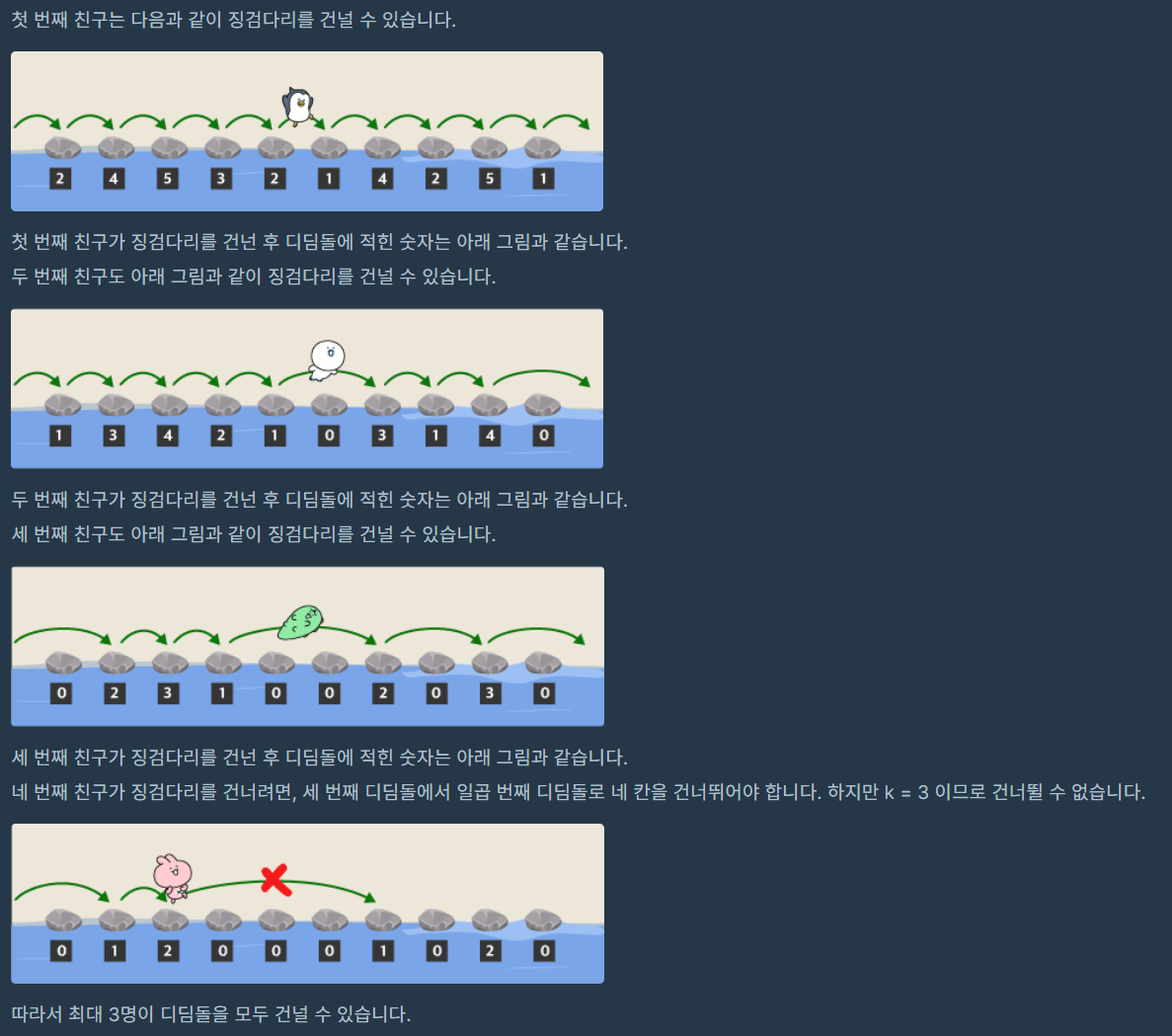
건널 수 있는 친구의 수를 1부터 최대 200000까지 구하면 비 효율적
따라서 1~ 200000 중앙 값부터 모두 건널 수 있는지 이분 탐색 시작
건널 수 없으면 중앙 값에서 좌측 절반, 건널 수 있으면 중앙 값에서 우측 절반 이동

✨ 트리

트리의 경우 DFS를 활용한 전/중/후위 순회, 루트노드, 서브트리, 높이, 너비, 그래프에서 트리의 수 찾기 등 다양하게 출제할 수 있다.
따라서 트리를 활용한 다양한 문제의 유형을 풀어보는 것이 좋다.
바킹독 트리 문제집의 문제들을 풀어보는 것을 추천한다.

✨ 그래프

최단 경로를 구하는 문제가 많이 출제된다.
최단 경로를 구할 때는 다익스트라, 벨만-포드, BFS, 플로이드-워셜 알고리즘들을 사용하자.
그래프 순회에는 DFS / BFS를 사용하자.
추가로 학습하면 좋은 알고리즘으로는 위상정렬이 있다.
예) 2021 KAKAO BLIND RECRUITMENT - 합승 택시 요금
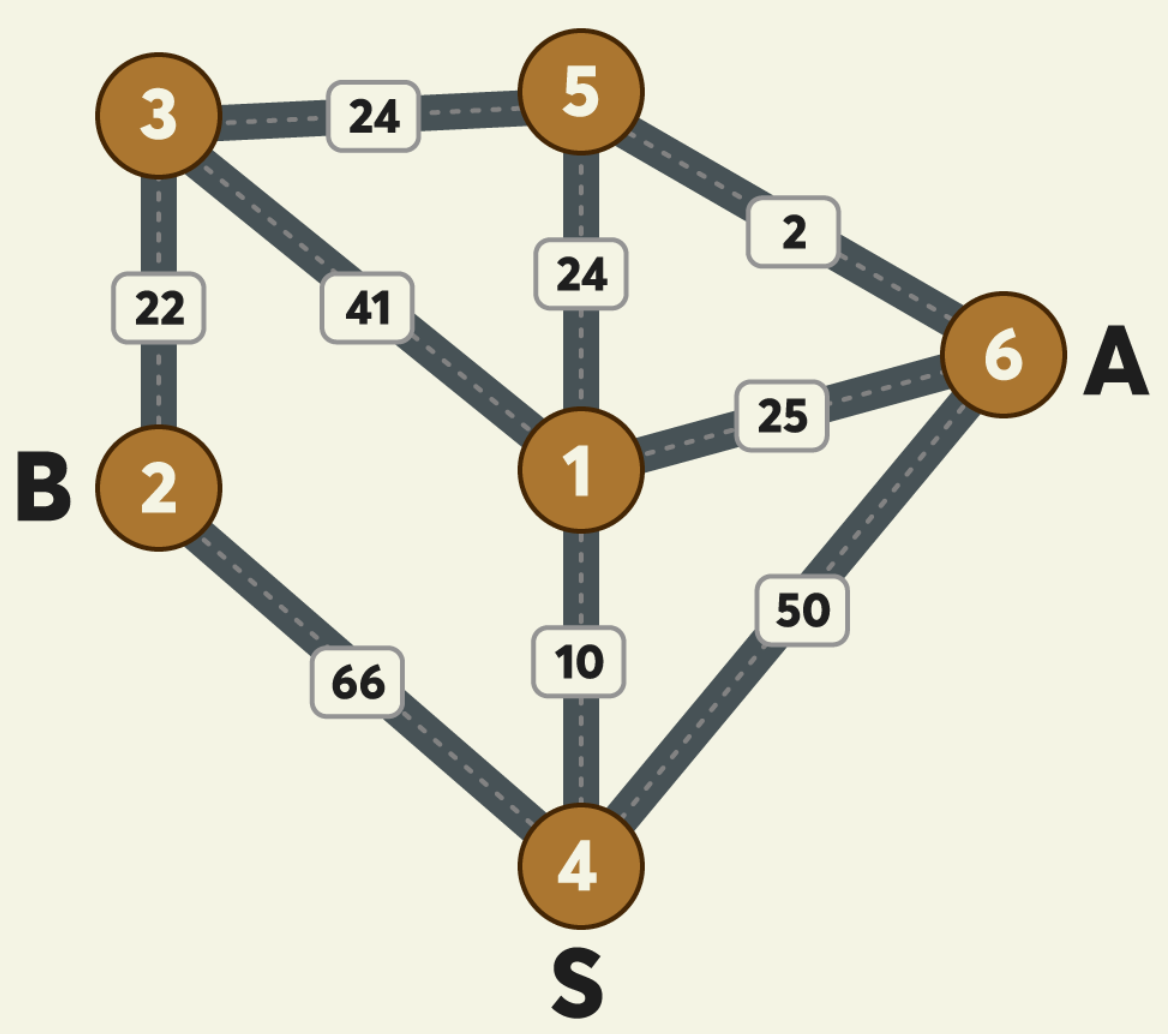
문제가 너무 길어서 사진만...
S에서 함께 출발하거나 따로 택시 타서 A, B에 각각 내리면 됨
즉, 어떤 정점(자신 포함)으로 까지의 최단 거리 + 해당 정점에서 A 최단 거리 + 해당 정점에서 B 최단 거리 3가지를 합친 것의 최소를 구하면 됨