탐욕(그리디) 알고리즘이란?
살면서 우리는 매번 선택을 해야 하는 상황에 직면하게 된다.
그 순간에 어떠한 선택을 하여야 할까?
현재의 즐거움을 따라서 선택하는 경우도 있고, 때로는 미래를 위해 현재의 만족을 포기하는 선택을 하기도 한다.
그런데 여기 '그리디'라고 현재의 즐거움만 고집하는 알고리즘이 있다.
매 순간마다 그 상황에서의 최적의 답을 선택하여 결과를 도출하는 알고리즘을 그리디 알고리즘이라고 한다.
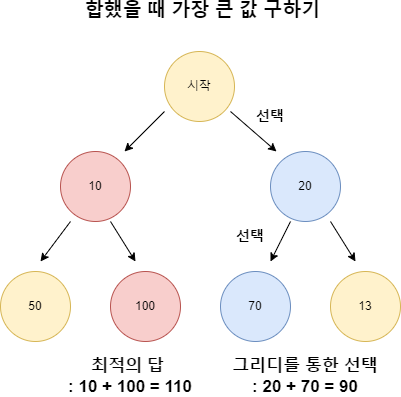
선택을 하는 순간에는 지금 이 순간, 지금 당장!! 최적으로 보이는 값을 선택하였다.
그러나, 최종적인 값을 봤을 때 그 값이 완전히 100% 최적의 값이 된다고는 할 수 없다.
이렇듯 나중은 생각하지 않고, 당장의 눈 앞에 보이는.. 그 순간에 가장 좋아보이는 것만을 쫒는 욕심을 부리기 때문에 욕심이 많다는 뜻의 그리디란 이름이 붙여진 듯하다.
🤷♀️ 그렇다면 최적의 값을 보장해주지 않음에도 불구하고 왜 사용하는 것인가?
앞서 말했듯이 최종적으로 가장 베스트인 값이 나오지 않을 수도 있다.
하지만!
부분적으로 보자면 어쨌든 그동안에 가장 좋은 답이라고 보여지는 값을 꾸준히 선택해왔기 때문에
최적에 가까운 그럴싸한 답을 도출해낼 수 있다.
(ex. 위의 그림을 보면 두 번째로 좋은 값인 90이 나오도록 선택된 것을 알 수 있다!)
또한, 이것저것 따지면서 여러 가지를 고려하는 게 아니라 오로지 그 순간에 가장 좋은 것!!!
딱 그것만 보고 선택하기 때문에 계산 속도가 빠르다.
특징
-
탐욕 선택 속성 : 현재 선택은 미래 선택에 영향을 줄 수 없다.
(이미 선택한 것을 뒤집을 수 없다. 다음 선택 시, 이전 선택이 별로인 것 같다고 생각되어 뒤로 돌아가서 다시 선택하거나 할 수 없다(선택 번복x)) -
최적 부분 구조 : 최적의 답을 도출하는 과정에 있어서 부분적으로는 최적의 답이 포함되어 있다.
-
항상 최적의 값이 나온다는 것을 보장하지 않는다.
(물론 그리디로도 100% 최적의 값이 나올 수 있다. 단, 항상 그런 것은 아니라는 점!
즉 그럴 수도 있고, 아닐 수도 있다.)
그리디 알고리즘 예시
📝 [ 가장 대표적인 그리디 문제 : 거스름돈 ]
거스름돈으로 사용할 동전의 종류 : 500원, 100원, 50원, 10원 존재
손님에게 거슬러줘야 할 돈이 3420원일 때, 최소한의 동전을 사용하여 거슬러주어라.
Q. 거스름돈으로 사용할 최소 동전 개수는?
❗ 최적의 방법 선택
- 최소한의 동전을 사용해야 하니 금액이 큰 동전부터 계산하여 거슬러줘야 한다.
매 선택 시, 최적의 선택은 500원 - 100원 - 50원 - 10원순이다.

- 답 : 총 12개 (6 + 4 + 0 + 2)
특이점
이 경우에는 각각의 동전들이 해당 동전보다 크기가 작은 동전들의 배수 형태였기 때문에 그리디 알고리즘으로 최적의 값을 구할 수 있었지만, 서로 배수 형태가 아닌 동전들이 무작위로 주어진다면 그리디로 풀 수 없다.
-
(1) 가능한 경우
앞선 예제는 50(원)은 10(원)의 배수, 100(원)은 50(원)의 배수, 500(원)은 100(원)의 배수였기 때문에 가능했다. -
(2) 불가능한 경우
이번에는 거스름돈이 240원이라고 하자.
그리고 거슬러줄 동전의 종류로는 100원, 80원, 20원 3가지가 있다.
(※ 100(원)은 80(원)의 배수가 아니다.)
👉 최적의 값 : 80원 x 3 = 240원으로 3개
👉 그리디 알고리즘 : 처음 선택 시 80원이 아니라 가장 좋은 선택으로서 100원을 선택.
계속 선택하다 보면 (100원 x 2) + (20원 x 2) = 240원으로 총 4개가 나온다.
따라서, 완전한 최적의 값이 나오지 않는다.
🤷♂️ 어떻게 그리디 알고리즘인지 알 수 있을까?
궁금하여 찾아보았는데....
- 그리디 알고리즘 유형의 문제는 매우 다양하기 때문에 암기한다고 해서 항상 잘 풀 수 있는 알고리즘 유형이 아니다. 많은 유형을 접해보고 문제를 풀어보며 훈련을 해야 한다.
- 특정한 문제를 만났을 때 단순히 현재 상황에서 가장 좋아 보이는 것만을 선택해도 문제를 풀 수 있는지를 파악할 수 있어야 한다.
- 그리디 알고리즘은 기준에 따라 좋은 것을 선택하는 알고리즘이므로 문제에서
'가장 큰 순서대로', '가장 작은 순서대로'와 같은 기준을 알게 모르게 제시해준다.
나동빈, 『이것이 취업을 위한 코딩 테스트다 with 파이썬』, 한빛미디어(2020), p 86-87.
문제를 보고... 그리디 알고리즘이다 하고 바로 알아채는 것은...
어려울 것 같기 때문에 그냥 문제를 많이 풀어보면서 자연스럽게 익힐 것...😬;;
.... 😂😂
