CS231n 강의 내용을 복습하기 위해 쓴 글입니다. 내용에 오류가 있을 시, 조언 및 지적해주시면 감사하겠습니다.

참조

CS231n 유튜브 강의
CS231n 강의 노트
https://doromi.tistory.com/112?category=849309

---

Loss Functions and Optimization

Reminder Previous Lecture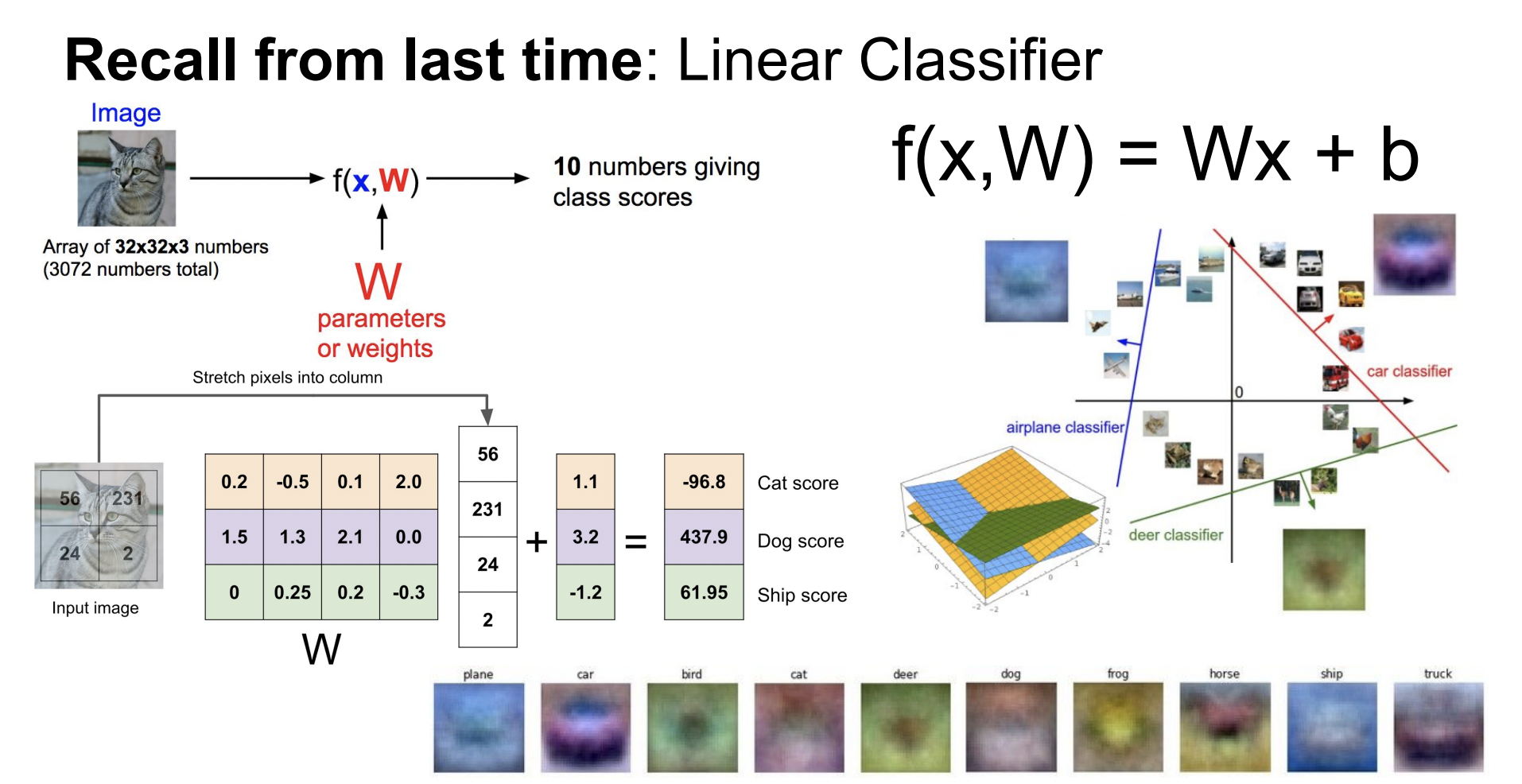

Linear Classification은 위와 같이 입력 이미지와 W값의 곱으로 생각할 수 있다. 이 결과는 클래스의 개수와 같은 차원을 가진다. 이 중 가장 큰 결과값을 가지는 클래스로 예측한다.
다음은 가중치 W값을 랜덤으로 설정한 뒤 3개의 이미지에서 얻은 결과이다. 이 중 2가지는 가장 큰 값이 나타나는 예측된 클래스가 정답 클래스와 일치하지 않은 것을 확인할 수 있다. 그렇다면 올바른 가중치 W값을 어떻게 찾는 것일까?

Loss Function

Loss Function: 손실함수라고 불리며, 현재 사용하고 있는 이미지 분류기(모델)가 얼마 만큼의 손실을 가지고 있는지를 나타내는 함수이다.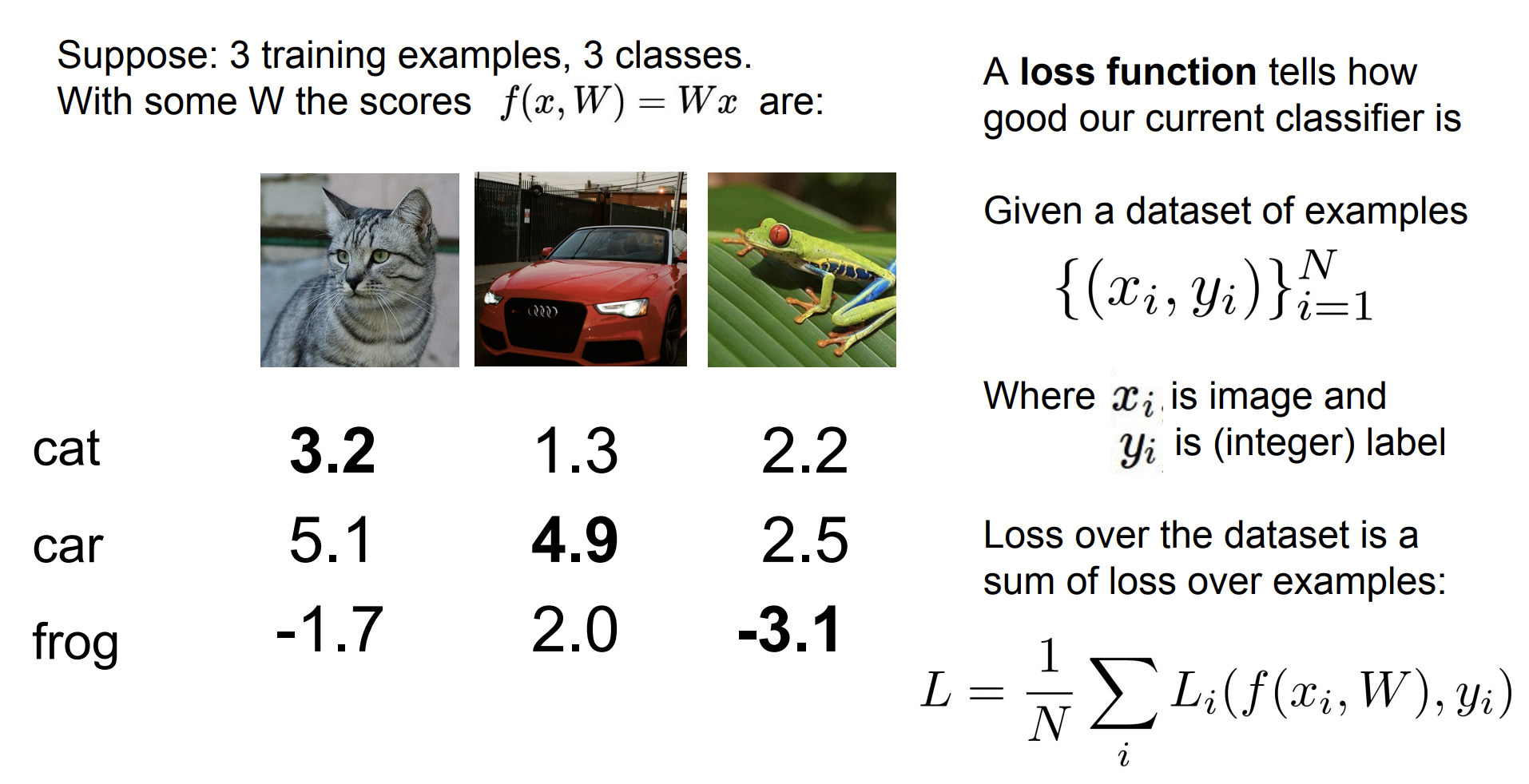어떤 Loss Function을 $L_{i}$라고 하자. 각 N개의 데이터에서 구해지는 손실값들을 더한 뒤 N으로 나눈 평균값을 Loss 값으로 사용하는 것을 확인할 수 있다. $L_{i}$ 함수에는 어떤 종류가 있는지 알아보자.

Multiclass SVM loss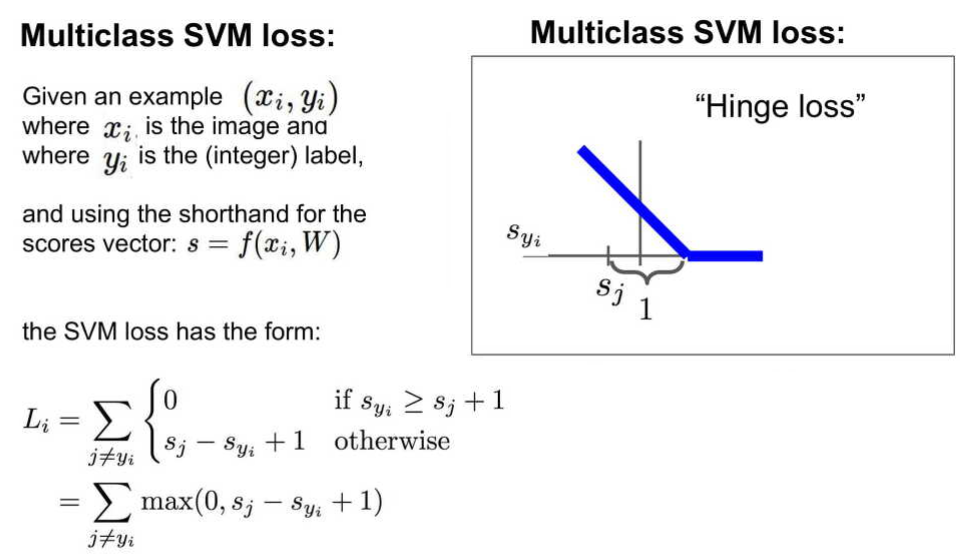

Multiclass SVM loss를 설명하자면 다음과 같다.

• Linear Classification인 $f(x_{i}, W)$ 에서 나온 결과를 $s$ 라고 하자.
• 정답인 클래스의 $s$ 값을 $s_{y_{i}}$라고 하고 나머지 클래스와 이 값을 비교한다.
• 정답인 클래스와 나머지를 비교했을 때, 정답보다 다른 클래스의 점수가 더 높다면 이 차이만큼이 Loss인 것이다.
• 위에서 구한 Loss값에서 safety margin이라는 값을 추가한다. 이는 정답 클래스가 적어도 다른 클래스보다 safety margin 값 만큼은 커야 한다는 의미이며 본 예시에서 safety margin = 1 이다.
• Loss 값이 0보다 작은 음수 값인 경우에는 포함하지 않는다.
• 위 그래프에서 가로축은 $s_{y_{i}}$ 값이고 세로축은 $L_{i}$의 값인 Loss 값을 표현하였다.

다음은 3개의 그림에 대한 Linear Classification 결과이다.
이 중 고양이 사진에 대한 Loss Function을 계산해보았다.
고양이는 3.2값을 가지며 나머지 자동차와 개구리에 대한 Loss 값은 다음과 같다.

• Loss(class:cat) = 0
• Loss(class:car) = max(0, 5.1-3.2+1) = 2.9
• Loss(class:frog) = max(0, -1.7-3.2+1) = 0
  고양이 사진의 전체 Loss = 0 + 2.9 + 0 = 2.9

나머지 두 사진도 위와 같은 방법으로 계산한다. 이 Loss 값들을 모두 더하고 사진 개수 만큼 나눈 값을 Multiclass SVM loss 라고 한다.

Multiclass SVM loss의 특징

• 정답 스코어가 safety margin = 1 을 만족하는 범위라면 Loss 값에 변화를 주지 않는다.
• 만약 Loss 값이 0이라고 할 때, W: weight parameter 값에 임의의 상수를 곱해도 Loss 값은 0이다.
• 위 점에서 Multiclass SVM loss는 유일하지 않다.
• 모든 $s$값이 0이라고 하면 Loss = class 수 - 1 값을 가진다. 이러한 특성은 Loss function의 작동을 Debug 하기에 적절하다.
• Loss의 최솟값은 0이며 최대값은 무한대이다.

Regularization

그렇다면 Loss function의 값이 줄어들수록 좋은 성능을 가질까?
정답은 '좋을 수도 있고 아닐 수도 있다' 이다.

Loss가 줄어든다는 것은 Train 데이터에 대해서 좋은 성능을 가지게 된다는 뜻이다.
하지만 이것은 Test 데이터에 대해 좋은 성능을 가진다는 것을 보장해 주지 않는다.
이 문제와 관련된 것이 바로 overfitting(과적합) 이다.

overfitting이란 Train 데이터에 대해서는 좋은 성능을 가지도록 학습되지만, Test 데이터에 대해서는 오히려 성능이 떨어지는 현상을 말한다.

그렇다면 이 문제를 어떻게 해결해야 할까? 정답은 Regularization 에 있다.
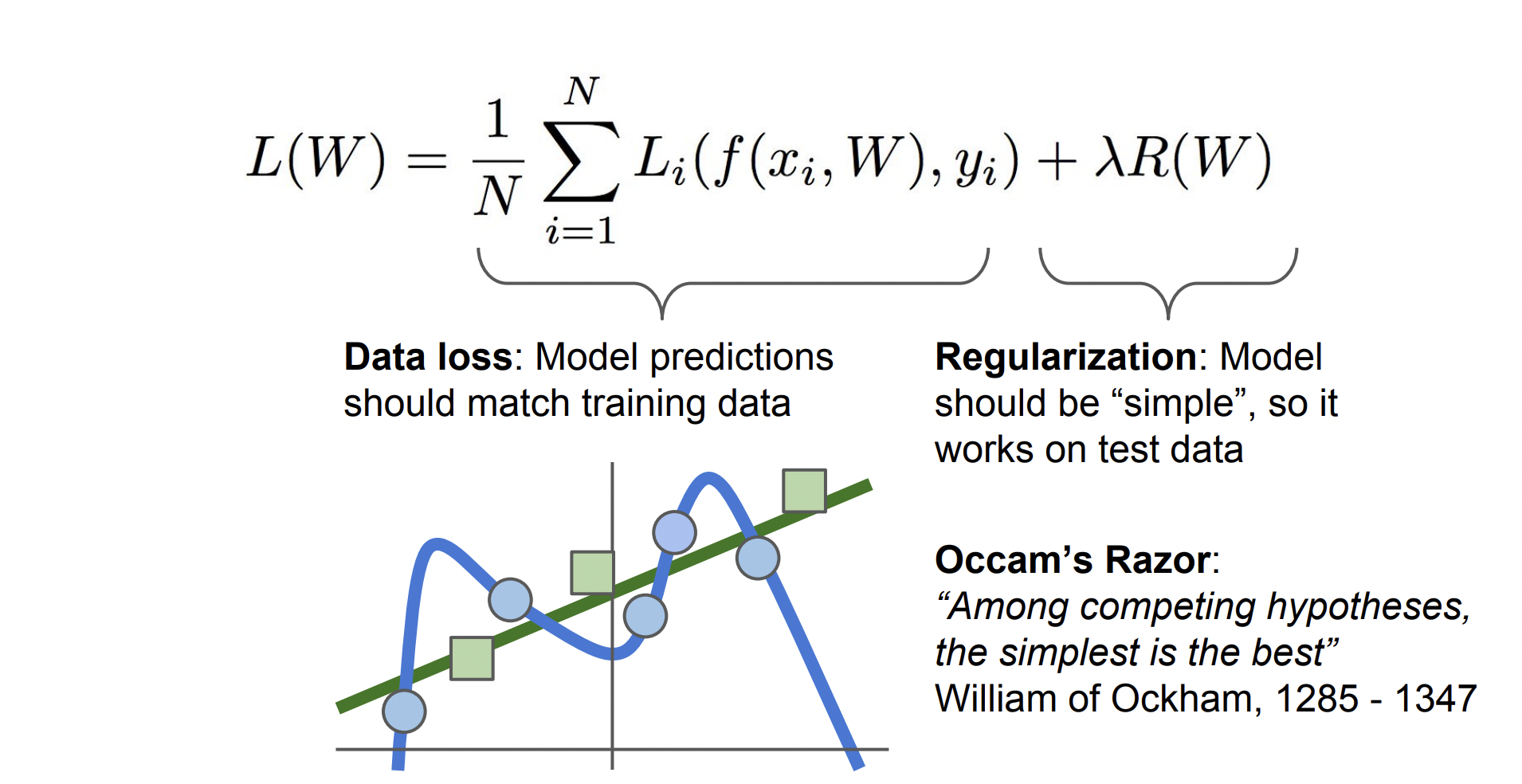Regularization 은 W 값에 제약을 가한다. 위 그림을 보면 파란색은 Train 데이터, 초록색은 Test 데이터이다. 예측한 파란색 선은 Train 데이터에 overfitting 되어 있는 것을 확인할 수 있다.

W의 값이 복잡한 값을 가지지 않게 하기 위해, W 값에 대해서 평가하는 함수를 추가하는 것을 Regularization 이라고 한다. Regularization 을 통해 모델은 더 단순한 W를 선택할 수 있다. (모델에 soft한 제약을 줌, penalty)

• "weight decay" : 특정 가중치가 비이상적으로 커지는 것을 방해하는것 이다.
• "local noise"와 outlier(특이점)의 영향을 적게 받도록 한다.

아래는 Regularization 에서 사용하는 function의 예시이다. 먼저 $\lambda$: Regularization strength 는 Regularization 값을 어느 정도로 사용할지를 정하는 값이고 그 이후 나오는 $R(W)$ 는 Regularization 함수이다. 종류는 L2 regularization, L1 regularization, Batch normalization, Elastic net, Dropout, Stochastic depth 등 다양한 Regularization 방법이 있다.

Train 데이터 $x$가 있고 서로 다른 $w$ 행렬 $\omega_{1}$과 $\omega_{2}$가 있다. $x$와 $w$의 내적을 구함으로써 Linear classification을 수행할 수 있다. Linear Classification 관점에서 $\omega_{1}$과 $\omega_{2}$는 같다.

$L_{1}$ 에서는 $\omega_{1}$ 을 선호한다. 왜냐하면, $L_{1}$ 은 행렬에서 0이 아닌 요소가 많을 때 복잡하다고 생각한다.

$L_{2}$ 에서는 $\omega_{2}$ 을 선호한다. 왜냐하면, $L_{2}$는 분류기의 복잡도를 각 값들이 얼마나 차이가 없는지로 비교하기 때문이다. Linear Classification에서 W는 얼마나 $x$가 output class와 비슷한지를 계산한다. 따라서 $L_{2}$는 변동이 심한 어떤 입력 $x$가 있고 그 특정요소에 의존하기 보다는 모든 $x$의 요소가 골고루 영향을 미치길 원할 때 사용한다.

어떤 문제를 가지고 있을 때, 그 문제에서 '복잡하다'를 어떻게 정의할 것인지를 고민하여 적절한 Regularization을 사용하는 것이 중요하다.

+) L1 regularization을 적용했을 때 두 weight 값은 같은 Loss를 가진다. 하지만 L2 regularization을 적용하면 $\omega_{1}$와 같은 경우는 1의 값을 가지지만, $\omega_{2}$와 같은 경우 4 x (1/4)^2 = 1/4 의 Loss를 가진다.

• L1 regularization

  • weight 값이 0으로 수렴하는 것이 많은 형태이다. 이를 Sparse matrix(희소행렬)이라고 부른다. 다시 말해, W 값이 희소행렬이 될 수 있도록 한다.
  • 위에서 0의 값이 많다는 이야기는 어떤 특징들을 무시하겠다는 것으로 볼 수 있다.

• L2 regularization

  • 가장 보편적인 방법으로 Euclidean Norm에 패널티를 주는 것이다.
  • weight 값이 큰 값은 점점 줄이며 대부분의 값들이 0의 가까운 값인 가우시안 분포를 가진다.
  • weight가 0이 아니라는 점에서 모든 특징들을 무시하지 않고 조금씩은 참고하겠다는 것으로 볼 수 있다.

• Elasticnet은 L1과 L2를 합친 것이다.

Softmax Classifier

Softmax는 스코어를 가지고 클래스별 확률 분포를 계산하는 방법이다.
또한, Multinomial Logistic Regression(다항 로지스틱 회귀)이라고도 불린다.

각 스코어에 지수를 취해 양수가 되게 만든 뒤에 지수들의 합으로 정규화를 한다. 이 과정을 통해, 확률 분포를 얻을 수 있고 이것이 바로 해당 클래스일 확률이 된다. 이 값은 확률이기 때문에 0-1 사이의 값을 가지며 모든 확률들의 합은 1이다. 정답 클래스의 확률값은 1에 가까운 값이며, Loss는 -log(해당 클래스일 확률) 로 정의된다.

손실함수는 얼마나 좋은지가 아니라 얼마나 '구린지'를 측정하는 것이기 때문에 log에 -를 붙인다. 해당 클래스 확률일 확률이 0에 가까울수록 loss값은 무한대로 커지고 1에 가까울수록 loss는 0에 가까워진다.

이론적으로 softmax의 최댓값은 무한대, 최솟값은 0이다. 하지만, 컴퓨터가 무한대 연산을 잘 못하기 때문에(유한정밀도) Loss가 0인 경우는 절대 없다.

스코어들이 모두 0근처에 모여 있는 작은 수일 경우 Loss는 어떻게 될까? 스코어들이 비슷하다면 -log(1/클래스 개수) 가 된다. (0에 가까운 스코어 값이 지수를 취해 지수들의 합으로 정규화하면 1에 가까운 확률값을 얻을 수 있음) log는 분자와 분모를 뒤집을 수 있기 때문에, 이점을 활용하면 log(클래스 개수) 가 된다. 이 점은 오류가 발생해 문제점을 찾고자 디버깅할 때 유용하다.

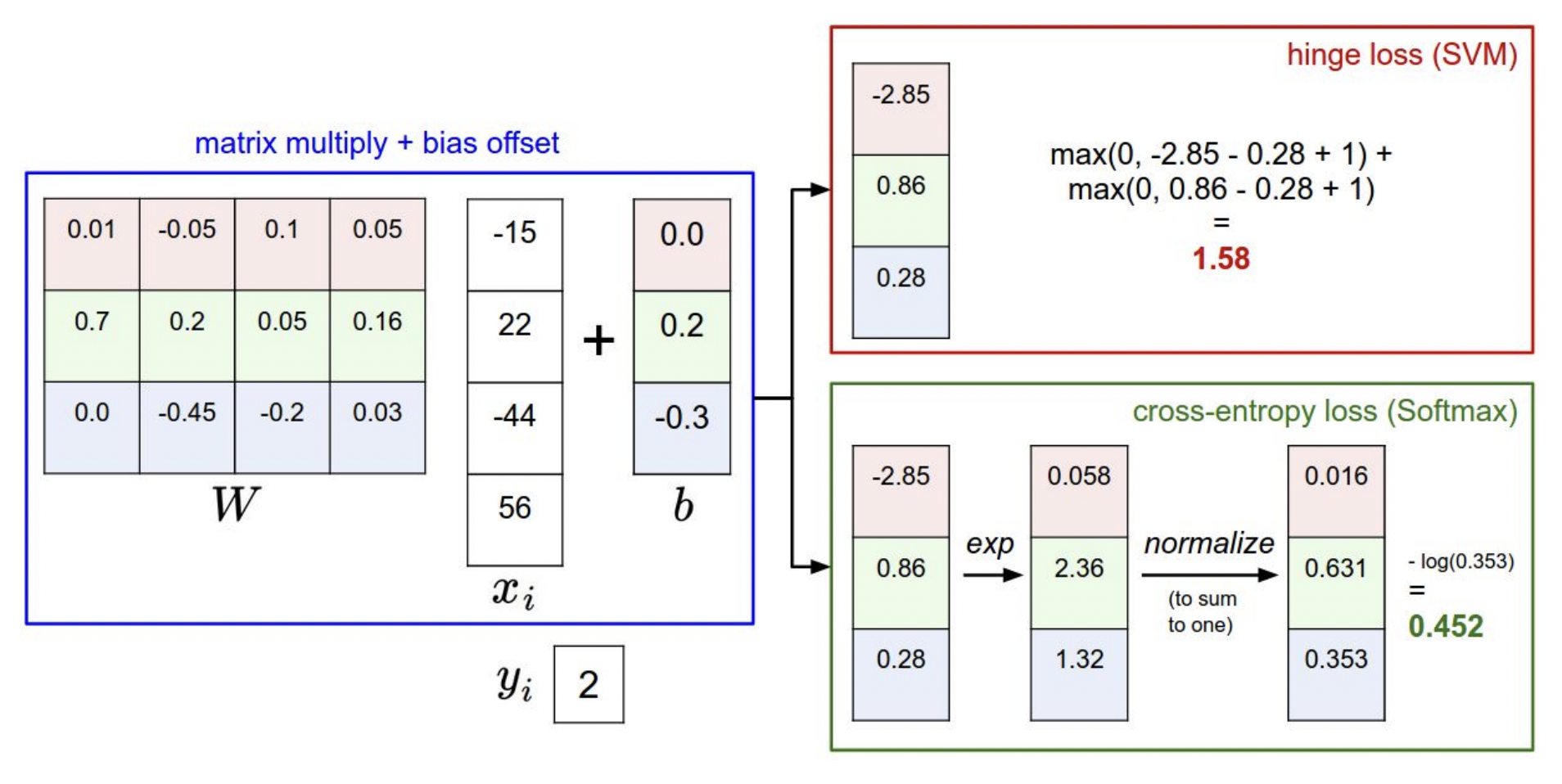SVM loss와 같은 형태는 hinge loss, Softmax의 경우 cross entropy loss 라고도 불린다.

SVM loss와 Softmax의 차이

• SVM loss는 정답과 그 외의 클래스 간 margin 만이 최종 결과값에 영향을 주기 때문에 스코어가 조금 변한다고 해서 SVM loss가 변하거나 하지 않는다.
• Softmax는 0-1 사이의 확률값만을 도출하기 때문에 정답 스코어가 충분히 높고 다른 클래스 스코어가 충분히 낮아도 최대한 정답 클래스에 확률을 몰아 넣으려고 한다.

다시 말해, SVM loss는 일정 margin만 넘기면 더이상 성능 개선에 신경을 쓰지 않는 반면, softmax는 계속해서 성능을 높이려고 노력한다.

Optimization

Loss를 줄이는 가중치 w를 찾는 것을 최적화라고 한다.

Random Search

아무런 기준 없이 무작위로 w값을 변경해보며 가장 좋은 성능을 가지는 값을 찾는 것이다. Random Search를 사용하면 약 15.5%의 성능을 가지는 것을 확인할 수 있으나 현재 최고 성능인 SOTA가 95%인 점을 보면 좋은 방법이 아니라는 걸 알 수 있다.

Local Geometry

기하학적 특성을 이용하여 최적화 방법을 수행할 수 있다.
눈을 감고 가장 낮은 지대를 찾아 걸어 이동할 때를 상상해보자. 우리는 발로 경사를 느끼고 어느 방향으로 내려가야 하는지를 직감적으로 알 수 있다. 경사를 느끼고 방향을 정해서 내려가는 것을 반복하다 보면 가장 낮은 지대를 찾을 수 있을 것이다. 이 방법은 NN이나 Linear Classifier를 훈련시킬 때 일반적으로 사용된다.

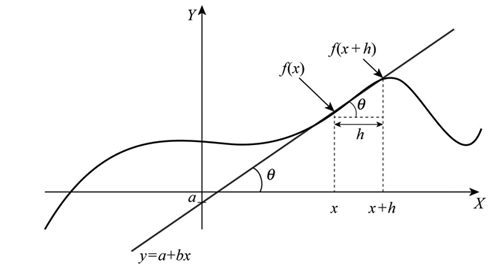어떤 점 x에서 도함수(derivative)를 계산해보면 작은 스텝 h가 있고 그 스텝 간의 함수 차이를 비교하기 위해 뺄셈을 하여 스텝 간격을 0에 가깝게 만들면 이것이 바로 그 점에서의 경사가 된다.

이 개념은 다변수 함수(multi-variable function)로도 확장시킬 수 있다. 실제로 x는 스칼라가 아니라 벡터로 x가 벡터이기 때문에 이 개념을 다변수로 확장시켜야 한다. 다변수인 상황에서 미분으로 일반화하면 gradient이고 gradient는 벡터 x의 각 요소의 편도함수들의 집합이다. (*편도함수는 독립변수가 2개 이상인 다변수함수에서의 도함수를 의미함) 입력이 3개면 gradient도 3개가 된다. gradient는 편도함수들의 벡터가 되고 방향은 함수에서 가장 많이 올라가는 방향이다.

특정 방향에서 얼마나 경사가 가파른지 알고 싶을 때 그 방향의 unit 벡터와 gradient 벡터를 내적하면 된다. gradient는 임의의 어떤 점에서의 선형 1차 근사 함수를 알려주기 때문에 많은 딥러닝 알고리즘들이 gradient를 계산하고 파라미터 벡터를 반복적으로 업데이트 하는 데에 사용한다.

컴퓨터로 gradient를 유용하게 사용할 수 있는 방법은 유한차분법(finite difference method)를 이용하는 것이다. 예시를 보면, 벡터의 두 번째 요소에 아주 작은 값 h(0.0001)을 더하고 loss를 구해보자. 기존 w에서의 loss와 h를 더했을 때의 loss의 차이를 계산하여 위 식에 나온 것처럼 극한 값을 이용해 gradient를 구할 수 있다. 이것을 각 요소마다 반복하면 된다.
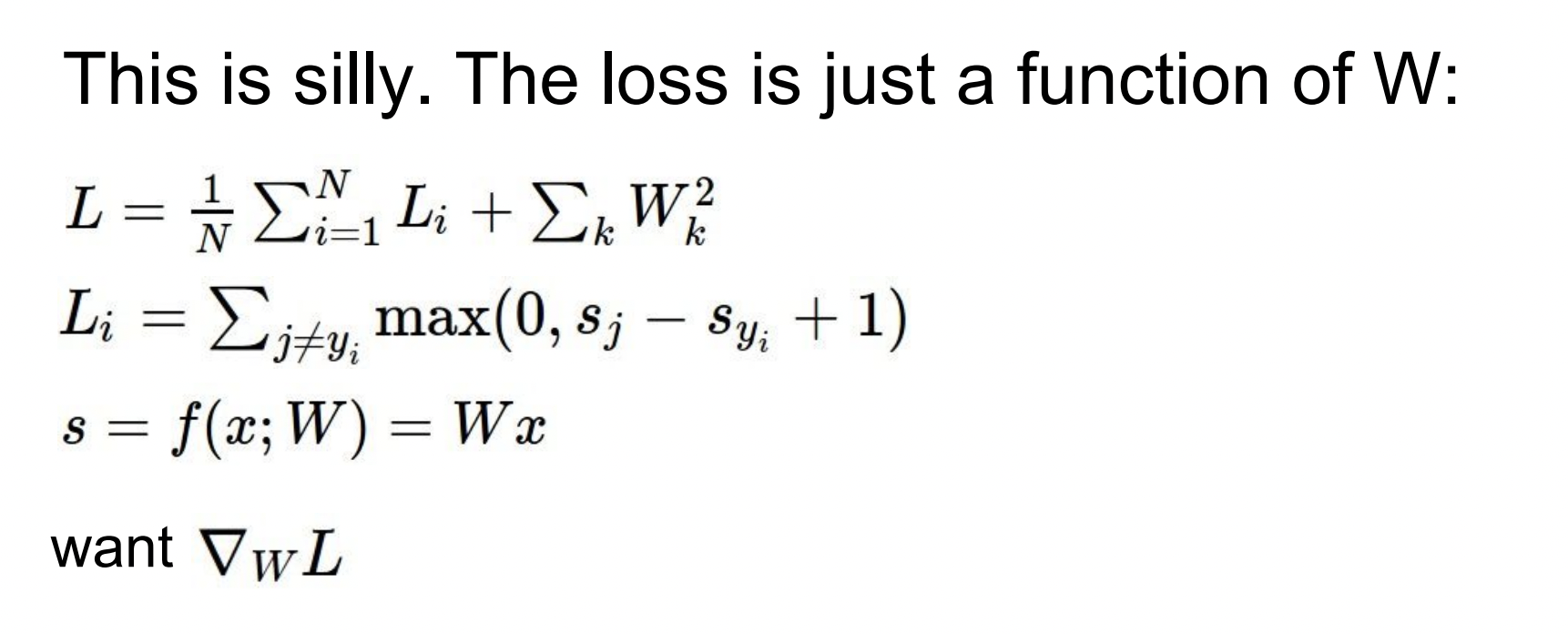벡터 요소마다 반복해서 수행하면 시간이 많이 걸리지만, 미분을 이용하면 바로 gradient를 수할 수 있다.

얻은 gradient의 반대 방향으로 w를 업데이트하고 아주 조금씩 이동하여 loss가 최저인 지점에 수렴하게 하는 것이 목표이다. step size를 정하는 하이퍼파라미터 learning rate를 올바른 값으로 설정하는 것도 중요하다.

손실함수를 정의한 것을 생각해보면, Loss를 구할 때 전체 Train 데이터 세트의 loss 평균으로 사용하였다. 하지만 실제로는 데이터의 개수 N이 매우 커질 수 있기 때문에 시간이 오래 걸리게 된다. (ImageNet의 경우 데이터 수가 130만개)

gradient를 계산하는 과정을 살펴보면 Loss는 그저 각 데이터의 loss의 gradient 합이라는 것을 알 수 있다. 그렇기 때문에 N개의 전체 Train 데이터 세트를 한 번 더 돌면서 계산해야 한다. 그래서 실제로는 Stochastic Gradient Descent 방식을 사용한다.

Stochastic Gradient Descent

전체 데이터 세트의 gradient와 loss를 계산하기 보다는 Minibatch라는 작은 트레이닝 샘플로 나누어서 학습하는 방식이다. 보통 2의 제곱으로 정해지며 32,64,128를 주로 쓰는 편이다. Minibatch를 이용하여, Loss의 전체 합의 추정치와 실제 gradient의 추정치를 계산할 수 있다. SGD 방식은 거의 모든 DNN 알고리즘에서 사용되는 기본적인 학습 알고리즘이다.

특징 변환

Linear Classification은 이미지에서 좋은 방법은 아니다. 그래서 DNN이 유행하기 전에는 Linear Classification을 이용하기 위해 두가지 과정을 거쳤다.

1. 이미지의 여러가지 특징표현을 계산
: 모양새, 컬러 히스토그램, edge 형태와 같은 특징 표현을 연결한 특징벡터
2. 이 특징벡터를 Linear Classification의 입력값으로 사용

컬러 히스토그램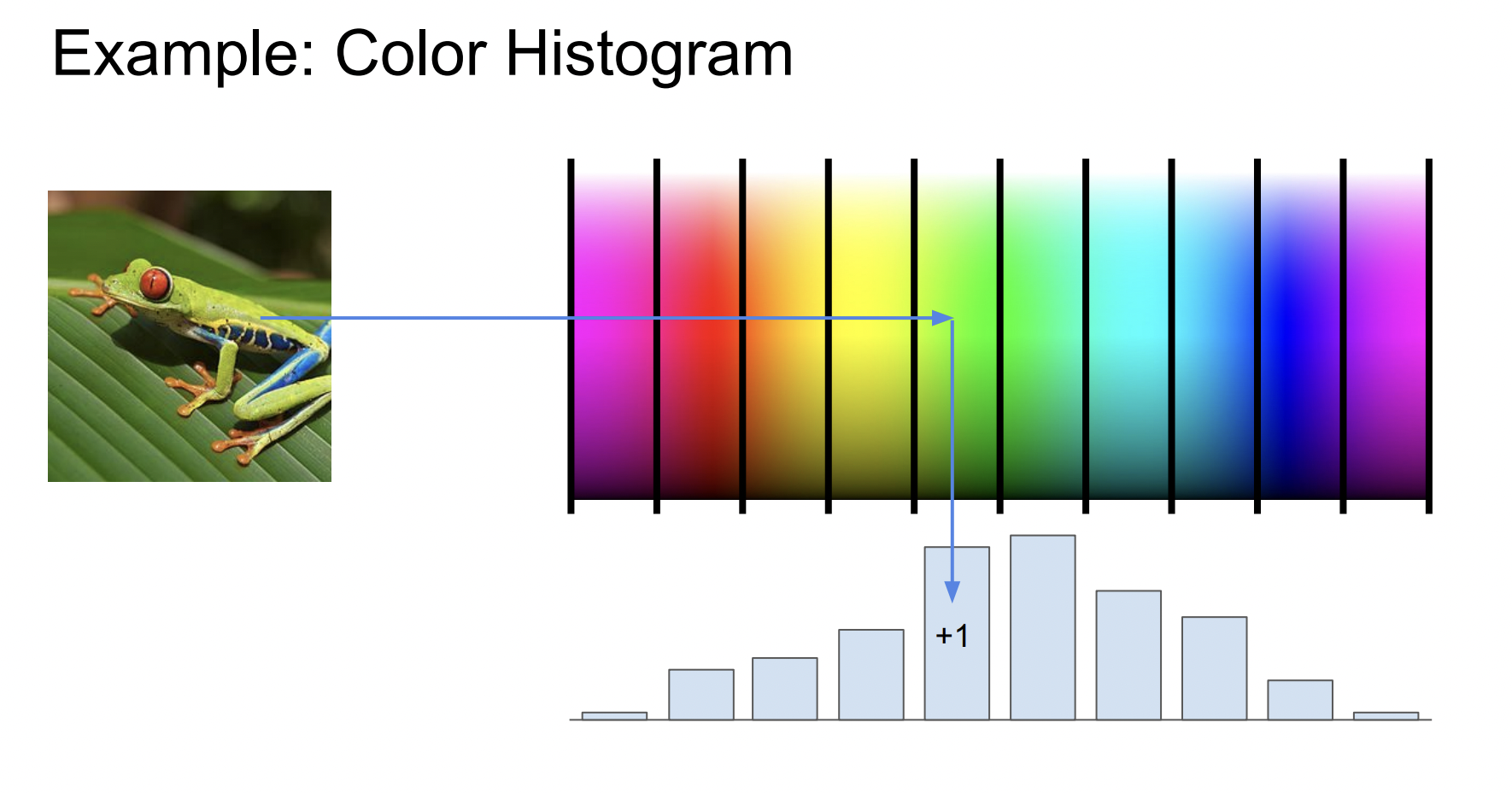

각 이미지에서 Hue 값만을 뽑아 각 색깔별 픽셀의 개수 를 세는 것이다. 개구리의 경우 초록색이 많음을 볼 수 있다.

Histogram of Oriented Gradient

이미지를 8*8 픽셀로 나눠서 각 픽셀의 지배적인 edge 방향을 계산한다.

Bag of Words

NLP에서 영감을 받은 방식으로 어떤 문장에서 여러 단어들의 발생 빈도를 세서 특징벡터로 사용하는 방식을 이미지에 적용한 것이다. 이미지들을 임의로 조각내고 각 조각들을 k-means 알고리즘을 이용해 군집화한다. 다양하게 구성된 각 군집들은 다양한 색과 다양한 방향에 대한 edge도 포착할 수 있다. 이러한 것들을 시각 단어(visual words)라고 부른다.

5-10년 전에는 대부분 이렇게 특징 벡터를 뽑아 Linear Classification의 input으로 사용하였다. 이 개념들은 CNN과 DNN으로 넘어간다고 크게 달라지지 않는다. 유일하게 다른 점이 있다면, 이미 만들어 놓은 특징을 쓰기 보다는 데이터로부터 특징을 직접 학습하려 한다는 점이다.