확률

인공지능 연구의 기반이 되는 선수과목, '확률및통계' 내용을 복습하기 위해 쓴 글입니다. 내용에 오류가 있을 시, 조언 및 지적해주시면 감사하겠습니다.

1.1 사건

• 통계적 실험(statistical experiment): 통계적 목적 아래 관찰이나 측정을 얻어내는 일련의 과정

• 관찰값(observation): 측정되거나 관찰된 값

• 표본공간(sample space): 측정 가능한 모든 결과들의 집합

  • sample space을 이루는 개개의 실험 결과를 element 또는 sample point라고 함
  • 추출 방법에 따라 비복원추출(without replacement), 복원추출(replacement)로 나눠짐

• 사건(event): 표본 공간의 부분집합으로 어떤 조건을 만족하는 특정한 표본점들의 집합

  • 하나의 표본점으로 구성된 사건 ➡️ 단순사건(simple event), 근원사건(elementary event)
  • 두 개의 표본점으로 구성된 사건 ➡️ 복합사건(compound event)
  • 표본점이 하나도 들어있지 않은 사건 ➡️ 공사건(empty event)
  • $A \cup B$ ➡️ A와 B의 합사건(union of events)
  • $A \cap B$ ➡️ A와 B의 공집합(intersection of events)
  • $A - B$ ➡️ A에는 있으나 B에는 없는 차사건(difference of events)
  • $A^c$ ➡️ A 안에 있지 않은 표본점으로 구성된 여사건(complementary event)
    
  • $A \cap B= \emptyset$ ➡️ 공통의 표본점을 갖지 않음. 배반사건(exclusive),
    • n 개의 사건 중에서 쌍마다 배반사건(pairwisely mutually exclusive)일 경우도 존재함, 이 합 사건이 표본공간 S인 사건을 분할(partition)이라 함

1.2 확률

• 확률(probability): 동일한 조건 아래서 동일한 실험을 무수히 반복하여 실시할 때, 어떤 특정한 사건이 발생하는 비율
  

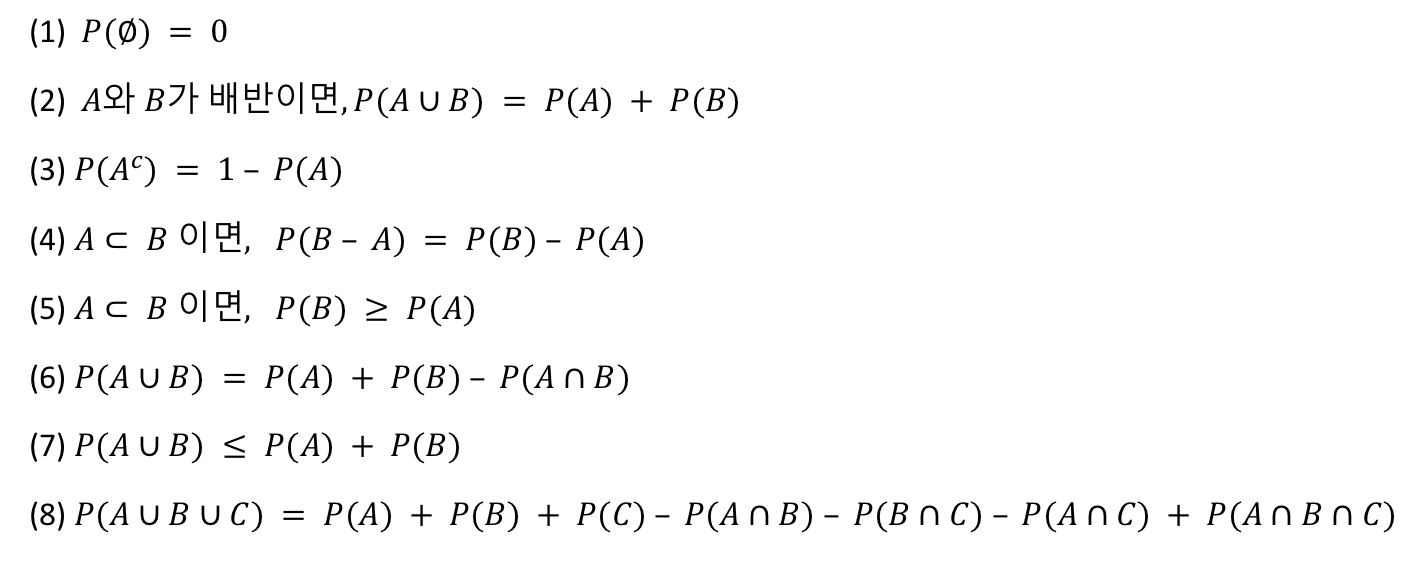
• 조건부 확률: P(A) > 0 인 어떤 사건 A가 주어졌다는 조건 아래서, 사건 B가 나타날 확률

  • $P(A \cap B)=P(A)P(B|A)$

  • $P(A \cap B \cap C)=P(A \cap B)P(C|A \cap B)=P(A)P(B|A)P(C|A \cap B)$

  • P(A) > 0 또는 P(B) > 0 일 때 사건 A의 발생여부가 사건 B의 발생에 영향을 미치지 않는 경우 ➡️ A와 B는 독립(independent)

    • $P(A \cap B)=P(A)P(B)$
    • $P(A|B)=P(A), P(B|A)=P(B)$

  • 독립이 아닌 경우 ➡️ A와 B는 종속(dependent)

1.3 베이즈 정리

• 전확률 공식(formula of total probability)
  
• 베이즈 정리(Bayes' theorem)
  
  • 베이즈 정리는 사전확률을 통해 더 많은 정보를 수집하는 수단으로 사용될 수 있다는 점에서 중요함