소개

딥러닝 관련 공부를 하다가 연구원 인턴이 되었고, 어느새 정직원이 되어 생성모델과 관련된 지식을 접하게 되었다. 깊게 공부는 하지 않았지만 딥러닝을 하며 느낀 점은 '수학이 그렇게 필요하지 않았다'라는 착각을 가지고 있었고, 생성모델을 보면서 이 착각은 완전히 잘못되었다고 느껴졌다.

생성모델에 대해 공부하고 논문을 보면 수식이 나오는데 이걸 볼때마다 진짜 큰 거부감이 느껴지며 참고 읽는다해도 이해하지 못해 좌절감만 느껴진다.

생성모델하면 기본적인 것이 무엇이냐고 누군가 물어본다면 '확률'이라는 답이 바로 나올 것 같다.

그만큼 생성모델에 관련된 논문을 볼때마다 확률변수, 확률분포 등 확률이란 단어만 해도 수도 없이 보게 되었고, 이 마저도 쉽게 이해되지 않았다.

앞으로도 계속 보게 될 확률에 대해 이해를 하고 싶어 계속 생각하다 보니 무언가를 깨닫게 되었다.

물론 하루 아침에 논문의 수식을 이해할 수 있는 수준에 도달한 것은 아니지만, 나와 같은 어려움을 겪는 사람들이 있을 것 같아 이 글을 쓰게 되었다.

확률의 예시

지금까지 대충 이해한 확률은 '특정 사건이 발생할 가능성' 정도로만 이해하였고 실제 정의도 그렇다.

이에 대한 흔한 예시로 동전 던지기가 있다.

동전의 앞면이 나올 확률은 1/2야, 앞면과 뒷면 중에 하나가 나올 확률이니까.

확률과 통계를 공부하면서 정말 많이 들어본 간단하고 직관적인 예시지만 나에게는 큰 독이 되었다.

사건은 앞면 혹은 뒷면이고, 1/2는 가능성이구나!

여기서 큰 문제점은 사건과 가능성이라는 정의에만 집중을 한다는 것이고, 이 이상의 사건과 가능성의 관계에 대해서는 한 번도 생각하지 않았다는 것이다.

확률, 그리고 함수

확률을 배울 때 이미 확률 질량 함수, 확률 밀도 함수와 같이 '함수' 라는 개념을 많이 들어왔지만, 그동안 '정의'에만 집중을 해왔던 나에게 '함수'라는 단어는 크게 중요하지 않아졌다.

그저 'A라는 사건이 일어날 확률'으로만 해석해왔고 이게 함수라는 개념이라고는 생각하지 않았으며, 실제로 큰 문제가 되진 않았었다. (고등학교때 봐왔던 확률 문제에서는 사건 자체를 묘사하는 문제가 많았었다...)

확률은 함수로 표현이 가능한 것이다.

확률을 함수로 이해하면 확률의 개념을 더 깊이 이해할 수 있다. 함수는 입력과 출력 간의 관계를 나타낸다. 확률 함수는 어떤 사건이 발생할 확률을 나타내는 함수이다. 이는 특정 사건이 일어날 가능성을 함수로 나타낸 것인데, 이 함수가 주어진 입력(사건)에 대해 출력을 확률로 반환한다는 의미이다.

예를 들어, 확률 질량 함수(Probability Mass Function)는 이산 확률 변수의 각 가능한 값에 대해 그 값이 일어날 확률을 나타낸다. 확률 밀도 함수(Probability Density Function)는 연속 확률 변수의 각 값에 대해 그 값이 일어날 가능성을 나타낸다. 두 함수는 모두 확률 분포를 나타내는 함수로, 사건의 확률을 함수로 표현한 것이다.

간단한 예시로 이를 살펴보면 조금 더 이해하기 쉬울 것이다.

확률 질량 함수

확률 질량 함수에서 가장 흔한 예시로 동전 뒤집기의 경우에서 확률 변수를 동전이 앞면인 경우를 1 뒷면인 경우를 0이라고 할 때, 확률을 함수로 표현하면 다음과 같다.

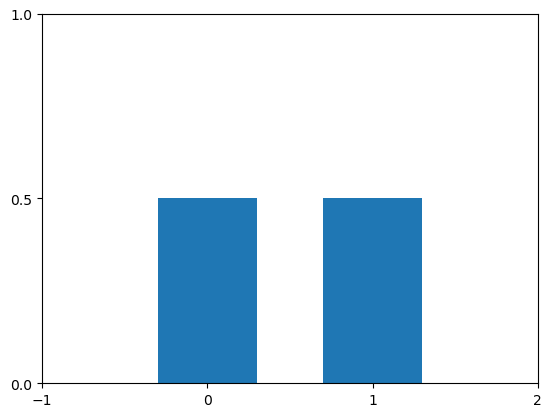
확률 밀도 함수

그럼 반대로, 확률 밀도 함수에서 가장 흔한 예시인 정규 분포를 예시로 든다고 할 때 이를 함수로 표현하면 다음과 같다.

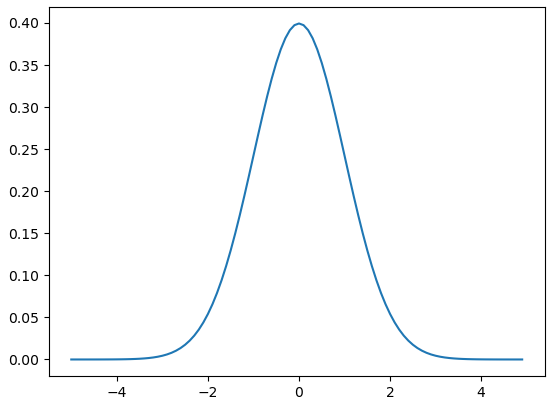
확률과 생성모델

지금까지의 생성모델에서는 어떤 데이터를 생성하고자 할 때, 주어진 상태에서 '높은 확률'을 가진 데이터를 생성하도록 학습이 진행되고 있다.

아주 간단한 예를 들면 '나는 밥을' 뒤에 올 단어를 예측한다고 할 때에는 '먹는다', '먹었다'와 같이 높은 확률로 올 단어를 선택하는 것과 유사하다고 보면 된다.

우리는 이 확률을 알기 위해서 '확률 분포'를 알아내야 한다.

확률 분포란?

확률 분포는 확률 변수 또는 확률 변수가 취할 수 있는 값들의 범위와 그 값들이 나타날 확률 간의 관계이다.

위 정의에서 보면 결국 '확률 변수와 그에 대한 확률 사이의 관계'라고 이해할 수 있고, 이는 '함수'로 표현할 수 있다는 것을 알 수 있다.

그럼 '그 함수'만 알면 분포를 알 수 있겠네?

그러나 '그 함수'를 알아내기에는 생각보다 많이 어려운 일이다.

실제로 이미지 생성과 같은 복잡한 문제의 경우에는 수많은 경우의 수가 존재하고 정규분포, 균등분포와 같이 간단한 분포로 나타나지 않을 가능성이 높다.

딥러닝

특정 데이터에 대한 분포가 어떤 함수로 표현이 될 수 있을지는 우리는 쉽게 알 수는 없지만 방법이 있다.

데이터가 주어지면 그에 맞는 함수를 제일 잘 찾아주는 딥러닝 방법론이다.

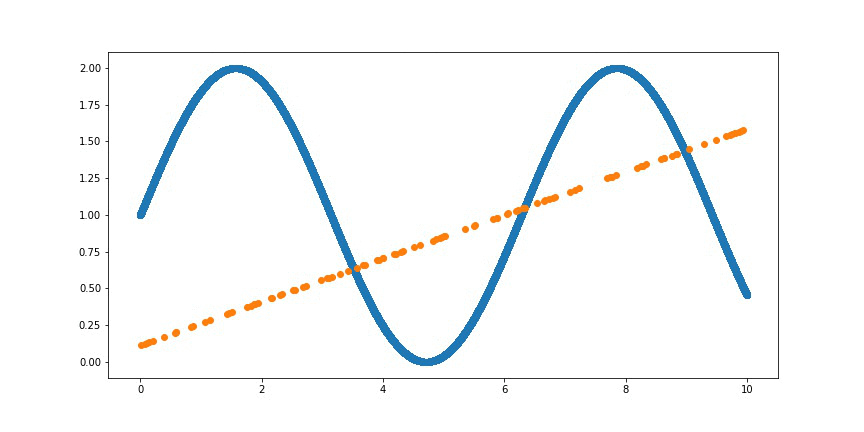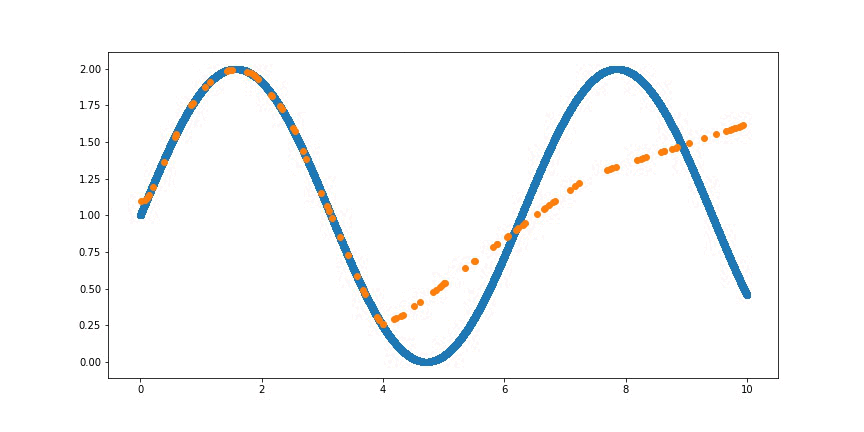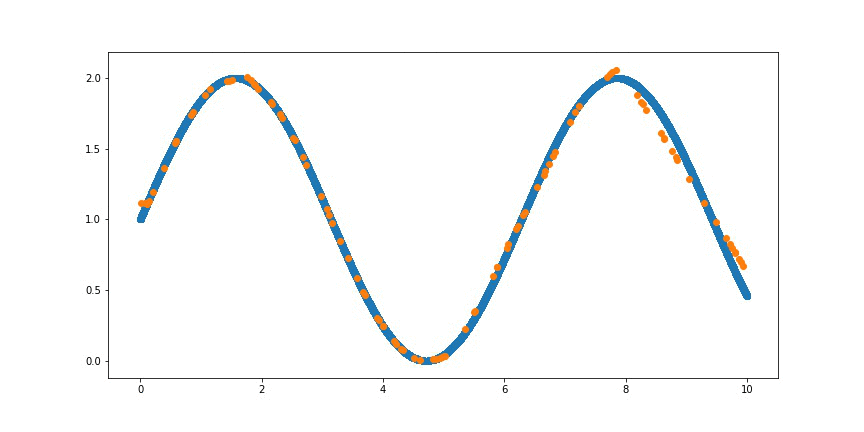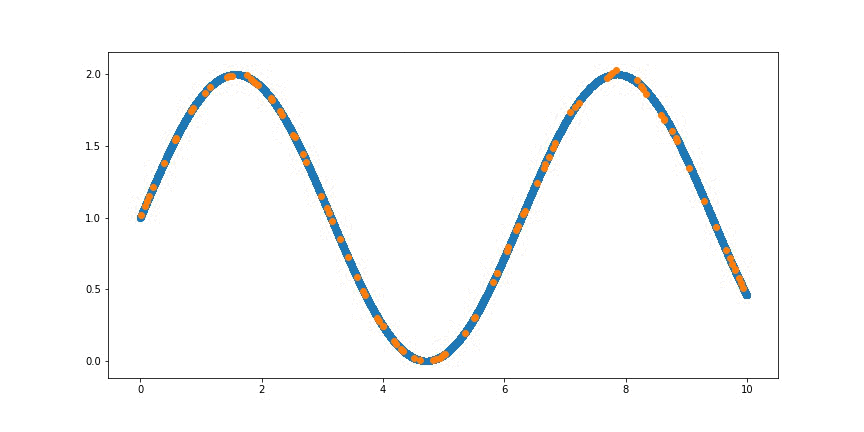
※ 출처 : Create animation of overfitting a Sin Wave with neural network - Medium

즉, 생성 모델을 학습하기 위해서는 데이터를 기반으로 확률 분포를 잘 설명할 수 있는 함수를 근사시키는 것이 목적이라는 것을 알 수 있다.

딥러닝에서는 이 분포를 근사하기 때문에 특정 조건에서 데이터를 어떻게 변화 시켜야 자연스러운지에 대해 알 수 있고, 이를 기반으로 데이터를 변화시켜 이미지, 텍스트, 오디오를 생성할 수 있게 되는 것이다.

결론

딥러닝과 생성모델을 공부하면서 확률에 대한 이해가 중요하다는 것을 깨달았다. 확률은 단순히 사건의 가능성을 나타내는 것이 아니라, 이를 함수로 표현하고, 확률 변수를 통해 사건의 결과를 수치적으로 나타내는 중요한 개념이다.

처음 생성 모델에 대해 공부할 때 '확률이 미분이 된다고?'라는 생각이 들면서 혼란스러웠다. 특히 스코어 함수(Score Function)와 같이 함수로 이해하는 것이 필수인 개념을 접할 때 더더욱 혼란스러웠다. 스코어 함수는 확률 밀도 함수의 로그를 미분한 것으로, 확률 분포의 모양을 이해하는 데 중요한 역할을 한다.

이런 이해를 바탕으로 기존의 논문들을 다시 보니 그래도 어떤 개념인지는 직관적으로 이해할 수 있게 되었다. 앞으로도 여러 가지 확률적인 개념을 더 깊이 이해하고자 노력해야겠다는 생각이 들었다.