[ Programmers ] 이중우선순위큐

Lutica_·2024년 7월 22일

coding test programmers

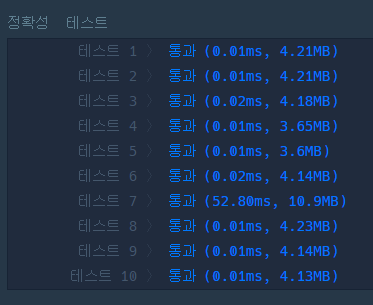
문제 풀기 : https://school.programmers.co.kr/learn/courses/30/lessons/42628

CPP 연습에 의의가 있다.

문제 접근

문제해석

아주 노골적으로 우선순위 큐가 있고, 그것이 이중으로 있다는 점에 착안한 문제이다.
따라서, 최댓값이나 최소값을 찾아서
멸령어 해석에 있어서 cpp언어라면 주의를 요한다!

Heap 과 우선순위 큐 의 개념

우선순위 큐

나오는데 순서가 있는 큐를 의미한다.
이는 보통 힙으로 구현한다.

Heap의 속성

힙은 tree에서 파생하여 나온 자료구조이다.
이는 특정한 방식에 의해 위계를 갖추고, 자식이 2개이하인 tree를 의미한다.
포화 이진트리의 경우 node수는 2^(n-1)개의 node를 가지고 있다. (n = 층계)

그러므로. 완전탐색으로 역값을 찾을 필요는 없다.
최솟값을 찾으려면, node/2까지만 탐색해도 된다.
왜나하면, 최대 heap에 의하면 가장 최대값은 leaf가까이 있기 때문이다.

문제 풀이

Cpp String 처리

#include <string> 을 도입해주어야 사용가능하다!

stoi -> string to int
substr(begin,size) -> begin~size 까지의 인덱스로 string을 자른다.

CPP에서의 Heap

#include <algorithm> 을 도입해주어야 사용가능하다!

push/pop

둘다 사용패턴은 아래와 같다.

somevector.push_back(...);
somevector.push_heap(somevector.begin(),somevector.end());

pop_heap(heap.begin(),heap.end());
heap.pop_back();

push_heap(it begin, it end) : begin~end 까지의 heap에 값을 삽입한다.
pop_heap ... : begin~end 까지의 heap에 맨 위값을 맨 뒤로 뺀다.

sort_heap 과 make_heap의 차이

make_heap : vector 자체를 힙으로 만든다. (기본값 최대힙)
sort_heap : 힙 자체를 재정렬하는데, 이때 어떤 연산자를 주지 않는다면 최소힙을 만든다
partial_sort : 힙기반 정렬. > 3개를 받는데 중간을 잘라서 정렬하는 함수이다.

참고 : https://programmerpsy.tistory.com/48

결합.

1. I로 시작하는 모든 명령어는 최대힙으로 삽입한다.
1. D 1은 최댓값을 찾아 제거한다.
1. D -1은 최솟값을 찾아서 제거하는데...
  
  최솟값을 찾기 위해서는, 위에서 최대 길이의 n/2까지만 돌아도 충분함을 보였으므로,
  그 범위내에서 가장 최솟값을 찾으면 된다.
1. 이후 다시 정리를 하고, 값을 돌려주면 된다.

코드


// 살짝 난잡하니 나중에 코드 정리하자...
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

vector<int> solution(vector<string> operations) {
    
    vector<int> heap = {};
    for(auto now = operations.begin(); now != operations.end(); now++)
    {
        string st = (*now);
        int val = stoi(st.substr(2,st.size()-2));
        if(st.at(0) == 'I')
        {
            heap.push_back(val);
            push_heap(heap.begin(),heap.end());
        }
        else if (st.at(0) != 'D') continue;
        else if (val == -1) 
        {
            if(heap.size() == 0) 
                continue;
            else if(heap.size() == 1) 
            {
                heap.erase(heap.begin());
                continue;
            }
            int min_check = *(heap.rbegin());
            int min_idx = heap.size()-1;
            for(int now = heap.size()-1; now >= heap.size()/2 ; now-- )
            {
                if(heap.at(now) < min_check)
                {
                    min_check = heap.at(now);
                    min_idx = now;
                }
            }
            heap.erase(heap.begin() + min_idx);
            make_heap(heap.begin(),heap.end());
        }
        else if (val == 1) 
        {
            if(heap.size() == 0) continue;
            pop_heap(heap.begin(),heap.end());
            heap.pop_back();
        }
    }
    vector<int> answer = {0,0};
    if(heap.size() == 0) 
        return answer;
    sort_heap(heap.begin(),heap.end());
    pop_heap(heap.begin(),heap.end()); 
    int min_check = *(heap.rbegin());
    int min_idx = heap.size()-1;
    int max_check = *(heap.begin());
    int max_idx = 0;
    if(heap.size() > 1)
    {
        for(int now = heap.size()-1; now >= heap.size()/2 ; now-- )
        {
            if(heap.at(now) < min_check)
            {
                min_check = heap.at(now);
                min_idx = now;
            }
        }
        for(int now = 0 ; now >= 2 ; now ++ )
            if(heap.at(now) > max_check) 
            {
                max_check = heap.at(now);
                max_idx = now;
            }
    }
    answer[0] = heap.at(max_idx);
    answer[1] = heap.at(min_idx);
    return answer;
}