Chater 12. 연산자 오버로딩

GoldenDusk·2024년 7월 31일

목록 보기

2/4

Chater 12. 연산자 오버로딩

01. 도입

2장에서 살펴본 망델브로 집합 플로터에서는 복수평명 위의 수를 표현하기 위해 num 트레이트의 Complex 타입을 사용한 예시가 아래와 같음

#[derive(Clone, Copy, Debug)]
struct Complex<T> {
	/// 복소수의 실수 부분
	re: T,
	/// 복소수의 허수 부분
	im: T,
}

보통 복소수의 형태는 a+bi 형식으로 나타낼 수 있으며, 여기서 a는 실수 부분이고 b는 허수 부분이다. T는 제네릭 타입으로, 실수 부분과 허수 부분이 다양한 수치 타입을 가질 수 있도록 한다.

예를 들어, 복소수 3+4i를 표현하기 위해 Complex 구조체를 사용할 수 있다.

let z = Complex { re: 3, im: 4 };

Complex 수는 기본 제공 수치 타입처럼 러스트의 +와 연산자로 더하고 곱할 수 있었다.

1. 연산자 오버로딩(operator overloading)이란?

연산자 오버로딩 : 사용자 정의 타입도 산술 연산자를 비롯한 여러 연산자를 지원 하는데 몇 가지 기본 트레이트를 구현하기만 되는 것을 말함

참고로 C++, C#, 파이썬, 루비의 연산자 오버로딩과 효과가 매우 비슷하다는 것으로 연산자 오버로딩을 위한 트레이트는 언어의 어떤 부분을 지원하는지에 따라 몇 가지 범주로 나뉜다.

이번 장의 목표는 이 장의 목표는 사용자 정의 타입을 언어에 잘 통합할 수 있도록 돕고, 이러한 연산자를 사용하는 타입에 가장 자연스럽게 작용하는 제네릭 함수를 작성하는 방법에 대해 이해를 돕는 것이다.

2. 연산자 오버로딩을 위한 트레이트

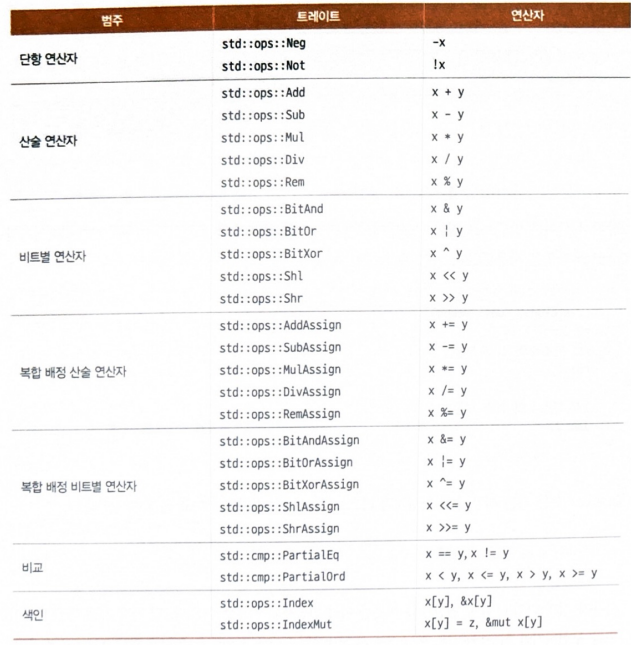
위의 표에 대한것들을 하나 하나 각자의 파트별로 조사해볼 예정!!

02. 산술 연산자와 비트별 연산자

트레이트 Add<T> T 값을 자기 자신에게 더하는 능력

1. add의 표현식

1) std::ops :: Add

러스트 표현식 a + b 는 a.add(b)로, 표준 라이브러리의 트레이트 std::ops::Add가 가진 메서드 add에 대한 호출 축약 표시이다. 표현식 a + b가 Complex 값에도 통하는 이유는 num 크레이트가 Complex에 이 트레이트를 구현해 두었기 때문이다.

다른 연산자의 경우에도 비슷하다. 예시로 a* b는 트레이트 std::ops: Mul이 가진 메서드 a.mul(b)의 축약 표기이고, std::ops :: Neg는 앞에 붙는 부호 부정 연산자를 담당한다.

Rust에서 연산자 오버로딩을 사용하는 방법을 설명하는 예시 코드

use std::ops::Add;
assert_eq!(4.125f32.add(5.75), 9.875);
assert_eq!(10.add(20), 30);

여기서 Add 트레이트를 사용하여 add 메서드를 호출해 숫자를 더하는 예이다. 4.125f32.add(5.75)는 4.125 + 5.75와 같은 결과를 가진다.

2) `std::ops::Add` 트레이트 정의

trait Add<Rhs=Self> {
    type Output;
    fn add(self, rhs: Rhs) -> Self::Output;
}

이 트레이트는 Rhs라는 타입 매개변수를 가지며 기본값은 Self이다.

Output은 덧셈의 결과 타입
이를 구현하면 + 연산자를 사용할 수 있게 된다.
add 메서드는 self와 rhs라는 두 개의 매개변수를 가진다.
- self는 메서드를 호출하는 값을 나타내며, rhs는 오른쪽 피연산자
- 이 메서드는 두 값을 더한 결과를 반환하며, 반환 타입은 Self::Output
- 즉, add 메서드는 self와 rhs를 더한 결과를 반환

3) 복소수 타입 Complex의 Add 트레이트 구현

복소수 타입인 Complex에 대해 Add 트레이트를 구현한 예로 Complex<i32> 타입의 값을 더하기 위해 Add<Complex<i32>> 트레이트를 구현해야 한다.

use std::ops::Add;

impl Add for Complex<i32> {
    type Output = Complex<i32>;

    fn add(self, rhs: Self) -> Self::Output {
        Complex {
            re: self.re + rhs.re,
            im: self.im + rhs.im,
        }
    }
}

같은 타입(self와 rhs가 Complex로 같은 타임)을 더하는 것이므로 그냥 Add라고만 사용하면 된다.

4) 다양한 `Complex` 타입에 대해 제네릭으로 Add 트레이트 구현

각각의 Complex, Complex, Complex 타입에 대해 Add 트레이트를 개별적으로 구현할 필요가 없다. 대신 제네릭을 사용하여 한 번에 모든 타입을 아우를 수 있다.

여러 타입에 대해 일반적으로 사용할 수 있도록 제네릭을 사용하는 예

use std::ops::Add;

impl<T> Add for Complex<T>
where
    T: Add<Output = T>,
{
    type Output = Self;

    fn add(self, rhs: Self) -> Self {
        Complex {
            re: self.re + rhs.re,
            im: self.im + rhs.im,
        }
    }
}

여기서 where T: Add<Output=T>는 타입 T가 덧셈이 가능하며 그 결과로 또 다른 T 타입을 반환한다는 것을 나타낸다. 이는 합리적인 제한이지만, 더 일반적인 제네릭 구현을 위해 조금 더 느슨하게 가져갈 수 있다.

5) 더욱 일반적인 제네릭 구현

왼쪽과 오른쪽 피연산자가 서로 다른 타입일 수 있도록 한 더 일반적인 제네릭 구현 예

use std::ops::Add;

impl<L, R> Add<Complex<R>> for Complex<L>
where
    L: Add<R>,
{
    type Output = Complex<L::Output>;

    fn add(self, rhs: Complex<R>) -> Self::Output {
        Complex {
            re: self.re + rhs.re,
            im: self.im + rhs.im,
        }
    }
}

6) 실제로 Rust에서의 제약

Rust는 다양한 타입이 섞여 있는 연산을 지원하지 않으려는 경향이 있다. 앞의 제네릭 구현에서 L과 R이 다를 수 있지만, 실제로는 대부분 같은 타입이 된다.

다른 조합을 구현하고 있는 타입 중에는 L로 사용할 수 있는 것이 많지 않기 때문에, 이러한 일반적인 제네릭 구현이 간단한 제네릭 정의보다 크게 유용하지 않을 수 있다.

7) 결론

Rust에서는 다양한 타입에 대해 연산자 오버로딩을 지원하여 사용자 정의 타입이 기본 제공 타입처럼 동작하도록 할 수 있다. 이를 통해 더 자연스럽고 읽기 쉬운 코드를 작성할 수 있으며, 제네릭을 사용하여 코드의 재사용성을 높일 수 있다.

Add 트레이트를 구현하면 사용자 정의 타입에서도 + 연산자를 사용할 수 있다.
Complex 타입에 대해 여러 타입을 지원하도록 제네릭으로 Add 트레이트를 구현할 수 있다.
Rust는 여러 타입을 섞어서 연산하는 것을 지원하는 데 제약이 있기 때문에, 이러한 제네릭 구현이 항상 유용하지 않을 수 있다.

2. 단항 연산자

1) 단항 연산자를 위한 기본 제공 트레이트

트레이트 이름	표현식	동등한 표현식
std::ops::Neg	-x	x.neg()
std::ops::Not	!x	x.not()

러스트의 부호 있는 수치 타입은 모두 단항 부호 부정 연산자 -를 위해서 std::ops ::Neg를 구현하
고 있고, 정수 타입과 bool은 단항 보수 연산자를 위해서 std::ops :: Not을 구현하고 있다.

!를 bool 값에 쓰면 값이 반대가 되지만, 정수에 쓰면 비트별 반전(즉, 비트 뒤집기)이 일어난다.

2) 트레이트 정의

trait Neg {
	type Output;
	fn neg(self) -> Self::Output;
}
trait Not {
	type Output;
	fn not(self) → Self::Output;
}

Neg 트레이트:
- type Output;: neg 메서드의 결과 타입을 정의합
- fn neg(self) -> Self::Output;: self의 부호를 부정한 결과를 반환
Not 트레이트:
- type Output;: not 메서드의 결과 타입을 정의합니다.
- fn not(self) -> Self::Output;: self의 논리 부정을 반환합니다.

3) 복소수의 부호 부정 구현

복소수의 부호 부정은 실수 부분과 허수 부분 각각의 부호를 부정하는 방식으로 구현된다. 이를 제네릭하게 구현하여 다양한 타입의 복소수를 지원할 수 있다.

use std::ops::Neg;

impl<T> Neg for Complex<T>
where
    T: Neg<Output = T>,
{
    type Output = Complex<T>;

    fn neg(self) -> Complex<T> {
        Complex {
            re: -self.re,
            im: -self.im,
        }
    }
}

4) 결론

Rust에서 연산자 오버로딩을 위해 Neg와 Not 트레이트를 사용한다.
Neg 트레이트는 부호 부정(-), Not 트레이트는 논리 부정(!) 연산자를 정의한다.
복소수(Complex<T>) 타입에 대해 Neg 트레이트를 제네릭하게 구현하여, 실수 부분과 허수 부분 각각의 부호를 부정할 수 있다.
이러한 구현을 통해 Complex 타입이 기본 제공 수치 타입처럼 부호 부정 연산을 지원하도록 할 수 있다.

3. 이항 연산자

1) 이항 연산자를 위한 기본 제공 트레이트 : 산술 연산자

범주	트레이트 이름	표현식	동등한 표현식
산술 연산자	std::ops::Add	x + y	x.add(y)
	std::ops::Sub	x - y	x.sub(y)
	std::ops::Mul	x * y	x.mul(y)
	std::ops::Div	x / y	x.div(y)
	std::ops::Rem	x % y	x.rem(y)

2) 이항 연산자를 위한 기본 제공 트레이트 : 비트별 연산자

범주	트레이트 이름	표현식	동등한 표현식
비트별 연산자	std::ops::BitAnd	x & y	x.bitand(y)
	std::ops::BitOr	`x	y`
	std::ops::BitXor	x ^ y	x.bitxor(y)
	std::ops::Shl	x << y	x.shl(y)
	std::ops::Shr	x >> y	x.shr(y)

3) 기본 제공 트레이트의 일반적인 형태

이항 연산자를 지원하는 트레이트들은 모두 동일한 일반적인 형태를 갖는다. 예를 들어, std::ops::BitXor 트레이트의 정의

trait BitXor<Rhs = Self> {
    type Output;
    fn bitxor(self, rhs: Rhs) -> Self::Output;
}

Rhs: 오른쪽 피연산자의 타입을 나타내며, 기본값은 Self이다.
Output: 연산의 결과 타입을 정의한다.
bitxor 메서드: self와 rhs를 받아서 Self::Output 타입의 결과를 반환한다.

4) Rust의 수치 및 비트 연산자

Rust의 수치 타입들은 모두 산술 연산자를 구현하고 있다.
정수 타입과 bool은 비트별 연산자를 구현하고 있다.
이러한 타입들의 레퍼런스를 한쪽 또는 양쪽 피연산자로 사용할 수 있게 하는 구현도 있다.

5) 문자열 연결에 대한 특이 사항

+ 연산자를 사용하여 String을 &str 슬라이스나 다른 String과 연결할 수 있다.
그러나 &str을 +의 왼쪽 피연산자로 사용할 수 없게 러스트가 막고 있기에, 짧은 문자열을 왼쪽에 거듭 연결하는 방식으로 긴 문자열을 쓸 수 없다.
여러 문자열을 하나로 합칠 때는 write! 매크로를 사용하는 것이 더 효율적이다. 이는 17장의 '텍스트 추가와 삽입' 절에서 자세히 다룬다.

4. 복합 배정 연산자

1) 복합 배정 연산자란?

복합 배정 표현식은 x += y나 x&= y와 같은 것을 말하며, 두 피연산자를 가지고 덧셈이나 비트별 논리곱 같은 연산을 수행한 뒤 결과를 다시 왼쪽 피연산자에 저장한다.

러스트에서 복합 배정 표현식의 값은 저장된 값이 아니라 항상 ()이다.

러스트는 접근법이 다르다. x += y는 그런 뜻이 아니라 메서드 호출 x.add_assign(y)의 축약 표기다. 여기서 add_assign은 std::ops :: AddAssign 트레이트가 가진 유일한 메서드다.

trait AddAssign<Rhs=Self>{
	fn add_assign(&mut self, rhs: Rhs);
}

2) 복합 배정 연산자를 위한 기본 제공 트레이트

범주	트레이트 이름	표현식	동등한 표현식
산술 연산자	std::ops::AddAssign	x += y	x.add_assign(y)
	std::ops::SubAssign	x -= y	x.sub_assign(y)
	std::ops::MulAssign	x *= y	x.mul_assign(y)
	std::ops::DivAssign	x /= y	x.div_assign(y)
	std::ops::RemAssign	x %= y	x.rem_assign(y)
비트별 연산자	std::ops::BitAndAssign	x &= y	x.bitand_assign(y)
	std::ops::BitOrAssign	`x	= y`
	std::ops::BitXorAssign	x ^= y	x.bitxor_assign(y)
	std::ops::ShlAssign	x <<= y	x.shl_assign(y)
	std::ops::ShrAssign	x >>= y	x.shr_assign(y)

3) Rust의 수치 타입과 정수 타입

Rust의 수치 타입들은 모두 산술 복합 배정 연산자를 구현하고 있다.
정수 타입과 bool 타입은 비트별 복합 배정 연산자를 구현하고 있다.

4) `Complex` 타입에 대한 `AddAssign` 트레이트 구현

use std::ops::AddAssign;

impl<T> AddAssign for Complex<T>
where
    T: AddAssign<T>,
{
    fn add_assign(&mut self, rhs: Complex<T>) {
        self.re += rhs.re;
        self.im += rhs.im;
    }
}

설명:

use std::ops::AddAssign; : 이 트레이트는 += 연산자를 정의한다.
impl AddAssign for Complex where T: AddAssign
- 제네릭 타입 T에 대해 Complex 타입의 AddAssign 트레이트를 구현한다.
- where T: AddAssign<T>는 타입 T가 AddAssign 트레이트를 구현해야 한다는 조건을 의미
fn add_assign(&mut self, rhs: Complex)
- add_assign 메서드는 &mut self와 rhs를 받아, Complex 값을 더한 결과를 self에 반영합니다.
self.re += rhs.re; self.im += rhs.im;
- self의 실수 부분(re)과 허수 부분(im)에 각각 rhs의 실수 부분과 허수 부분을 더한다.

5) 복합 배정 연산자 트레이트와 이항 연산자 트레이트의 관계

복합 배정 연산자를 위한 기본 제공 트레이트는 그에 상응하는 이항 연산자를 위한 트레이트와 완전히 별개이다.

예를 들어, std::ops::Add를 구현한다고 해서 std::ops::AddAssign이 자동으로 구현되지는 않는다.
만약 특정 타입을 += 연산자의 왼쪽 피연산자로 사용하고 싶다면, 해당 타입에 대해 직접 AddAssign을 구현해야 한다.

6) 결론

Complex 타입에 대해 제네릭으로 AddAssign 트레이트를 구현하여, 실수 부분과 허수 부분 각각에 대해 += 연산을 지원할 수 있다.
복합 배정 연산자 트레이트는 이항 연산자 트레이트와는 별개로 구현되어야 하며, 필요에 따라 각각을 명시적으로 구현해야 한다.

03. 동치비교

Rust에서 상등(==) 연산자와 같지 않음(!=) 연산자는 std::cmp::PartialEq 트레이트를 통해 정의된 eq와 ne 메서드를 호출하는 축약 표기

assert_eq!(x == y, x.eq(&y));
assert_eq!(x != y, x.ne(&y));

1. PartialEq

1) std::cmp::PartialEq의 정의

trait PartialEq<Rhs = Self>
where
    Rhs: ?Sized,
{
    fn eq(&self, other: &Rhs) -> bool;
    fn ne(&self, other: &Rhs) -> bool {
        !self.eq(other)
    }
}

eq 메서드는 두 값을 비교하여 같으면 true, 다르면 false를 반환
ne 메서드는 기본적으로 eq 메서드를 반대로 사용하여 정의된다. 즉, ne는 eq의 결과를 부정
즉, ne 메서드는 기본 정의가 있기 때문에 PartialEq 트레이트를 구현할 때는 eq만 정의하면 된다.

2) PartialEq 구현 예시 : Complex을 위한 완전한 구현

Complex 타입에 대한 PartialEq 트레이트를 구현하는 예시

impl<T: PartialEq> PartialEq for Complex<T> {
    fn eq(&self, other: &Complex<T>) -> bool {
        self.re == other.re && self.im == other.im
    }
}

이 구현은 임의의 구성 요소 타입 T에 대해 상등 비교가 가능한 Complex<T>를 위한 비교를 정의한다.
실수 부분(re)과 허수 부분(im)을 각각 비교하여 두 Complex 값이 같은지 확인한다.

3) PartialEq 구현의 자동 생성

PartialEq의 구현은 왼쪽 피연산자의 각 필드를 그에 대응하는 오른쪽 피연산자의 필드와 비교하는 게 전부라서 자주 쓰이는 연산임에도 이기에 PartialEq 자동 생성이 있다.

Rust는 요청이 있을 경우 PartialEq의 구현을 자동으로 생성해 준다. 다음과 같이 타입 정의에 derive 어트리뷰트를 추가하면 됨

#[derive(Clone, Copy, Debug, PartialEq)]
struct Complex<T> {
    re: T,
    im: T,
}

자동으로 생성되는 구현은 수작업으로 작성한 코드와 본질적으로 동일
모든 필드나 요소를 차례로 비교하여 상등성을 판단한다.

4) PartialEq와 Eq의 관계

PartialEq는 부분 동치 관계를 나타내며, 완전 동치 관계는 아니다.
완전 동치 관계를 나타내는 std::cmp::Eq 트레이트가 있으며, 이는 PartialEq의 확장의 의미

trait Eq: PartialEq<Self> {}

Eq를 구현하는 타입은 PartialEq를 구현해야 하며, x == x가 항상 true여야 합니다.
대부분의 타입은 PartialEq와 Eq를 모두 구현합니다. f32와 f64는 예외입니다.

2. 산술과 비트별 트레이트와 PartialEq

1) 산술과 비트별 트레이트와 PartialEq의 차이

산술 연산자와 비트 연산자:
- 피연산자를 값으로 받는다.
- 예: x + y, x & y
PartialEq 트레이트:
- 피연산자를 레퍼런스로 받습니다.
- 예: x == y, x != y
- 이는 String, Vec, HashMap 같은 비Copy 값을 비교할 때 이동이 발생하지 않음을 의미
- 비교만 했을 뿐인데 값이 이동된다면 예상치 못한 동작이 발생할 수 있다.

2) 산술과 비트별 트레이트와 PartialEq의 차이 예제 코드

let s = "d\x6fv\x65t\x61i\x6c".to_string();
let t = "\x640\x76e\x74a\x69l".to_string();
assert!(s == t); // s와 t는 차용될 뿐이다.
// 따라서 여기서도 값을 계속 사용할 수 있다.
assert_eq!(format!("{} {}", s, t), "dovetail dovetail");

이 예제에서 s와 t는 PartialEq 트레이트를 사용하여 비교됩
s와 t는 차용(borrow)되었으므로 값이 이동하지 않는다.

차용(borrow)와 값의 이동(move)의 차이

따라서 비교 후에도 s와 t를 계속 사용할 수 있다.

3) PartialEq 트레이트의 Rhs 타입 매개변수 : Rhs 타입 매개변수의 트레이트 바운드

where
	Rhs: ?Sized

PartialEq 트레이트의 정의

trait PartialEq<Rhs = Self>
where
    Rhs: ?Sized,
{
    fn eq(&self, other: &Rhs) -> bool;
    fn ne(&self, other: &Rhs) -> bool {
        !self.eq(other)
    }
}

Rhs: ?Sized:
- Rust는 보통 타입 매개변수가 균일 크기 타입이어야 한다고 요구한다.
- 그러나 ?Sized를 사용하면 비균일 크기 타입을 지원할 수 있다.
- 이를 통해 요건이 완화되어 PartialEq나 PartialEq<[T]> 같은 트레이트를 작성할 수 있다.

4) PartialEq의 사용 예

assert!("ungula" != "ungulate");
assert!("ungula".ne("ungulate"));

PartialEq 트레이트를 사용하여 문자열 비교를 수행합니다.
eq와 ne 메서드는 &Rhs 타입의 매개변수를 받으므로, &str나 &[T]와 비교해도 전혀 문제없다.
두 단언문은 동일한 의미를 가진다.

여기서 Self Rhs는 모두 비균일 크기 타입인 str이므로 ne의 self와 rhs 매개변수는 모두 &str값이 된다. 균일 크기 타입, 비균일 크기 타입. Sized 트레이트는 13장의 'Sized' 절에서 자세히 살펴본다.

3. 동치 관계와 부분 동치 관계

1) 동치 관계의 수학적 정의

동치 관계(equivalence relation)의 세 가지 요구 사항:

대칭성: x == y가 참이면 y == x도 참
전이성: x == y이고 y == z이면 x == z여야 한다.

일련의 값이 주어졌을 때, 각 값이 옆에 있는 값과 같다면 각 값은 나머지 모든 값과 같다. 상등성은 전염성이 있다.

반사성: x == x는 항상 참이어야 한다.

2) IEEE 표준 부동소수점 값과 NaN

Rust의 f32와 f64는 IEEE 표준 부동소수점 값을 사용한다.
이 표준에 따르면 NaN(특별한 수가 아님) 값은 자기 자신을 포함한 어떤 값과도 같지 않다고 취급

assert!(f64::is_nan(0.0/0.0));
assert_eq!(0.0/0.0 == 0.0/0.0, false);
assert_eq!(0.0/0.0 != 0.0/0.0, true);
assert_eq!(0.0/0.0 < 0.0/0.0, false);
assert_eq!(0.0/0.0 > 0.0/0.0, false);
assert_eq!(0.0/0.0 <= 0.0/0.0, false);
assert_eq!(0.0/0.0 >= 0.0/0.0, false);

NaN 값의 상등 및 순서 비교는 항상 거짓을 반환해야 한다.

Rust에서 동치 관계를 만족시키기 위해 PartialEq와 Eq 트레이트가 사용된다. 그러나, 이들 트레이트는 각각 부분 동치 관계와 완전 동치 관계를 나타낸다.

3) 부분 동치 관계 (Partial Equivalence Relation)

Rust의 == 연산자는 일반적으로 동치 관계의 세 가지 요구 사항 중 첫 번째와 두 번째를 만족한다.
첫 번째 요구 사항: 대칭성 - x == y가 참이면 y == x도 참이어야 한다.
두 번째 요구 사항: 전이성 - x == y이고 y == z이면 x == z여야 한다.
세 번째 요구 사항: 반사성 - x == x는 항상 참이어야 한다.

그러나, IEEE 부동소수점 값(예: f32와 f64)에 대해서는 세 번째 요구 사항인 반사성을 만족하지 못한다. 예를 들어, NaN 값은 자기 자신과도 같지 않다고 취급된다.

assert!(f64::is_nan(0.0/0.0));
assert_eq!(0.0/0.0 == 0.0/0.0, false);
assert_eq!(0.0/0.0 != 0.0/0.0, true);

이러한 이유로 PartialEq는 부분 동치 관계를 나타낸다.
PartialEq 트레이트는 두 값이 같은지 비교하기 위해 사용된다.

trait PartialEq<Rhs = Self>
where
    Rhs: ?Sized,
{
    fn eq(&self, other: &Rhs) -> bool;
    fn ne(&self, other: &Rhs) -> bool {
        !self.eq(other)
    }
}

eq 메서드는 두 값을 비교하여 같으면 true, 다르면 false를 반환한다.
ne 메서드는 기본적으로 eq 메서드를 반대로 사용하여 정의된다.

4) 완전 동치 관계 (Full Equivalence Relation)

완전 동치 관계는 세 가지 요구 사항을 모두 만족해야 한다.
Eq 트레이트는 완전 동치 관계를 나타내며, PartialEq의 확장으로 정의된다.

trait Eq: PartialEq<Self> {}

Eq를 구현하는 타입은 PartialEq도 구현해야 하며, x == x가 항상 true여야 한다.
대부분의 타입은 PartialEq와 Eq를 모두 구현한다. 예외적으로, f32와 f64는 PartialEq만 구현하고 Eq는 구현하지 않는다.

5) PartialEq의 구현 예

impl<T: PartialEq> PartialEq for Complex<T> {
    fn eq(&self, other: &Complex<T>) -> bool {
        self.re == other.re && self.im == other.im
    }
}

이 구현은 임의의 구성 요소 타입 T에 대해 상등 비교가 가능한 Complex<T>를 위한 비교를 한다고 함

5) Eq의 구현 예

impl<T: Eq> Eq for Complex<T> {}

Complex 타입에 대해 Eq를 구현하는 예입니다. 매우 간단하게 구현할 수 있다.

6) 자동 생성

Rust는 PartialEq와 Eq 트레이트의 구현을 자동으로 생성할 수 있다.

#[derive(Clone, Copy, Debug, Eq, PartialEq)]
struct Complex<T> {
    re: T,
    im: T,
}

derive 어트리뷰트를 사용하면, 필드나 요소를 차례로 비교하는 방식으로 상등성을 판단하는 구현이 자동으로 생성된다.
이 경우, Complex<i32>는 i32가 Eq를 구현하므로 Eq를 구현하지만, Complex<f32>는 f32가 Eq를 구현하지 않으므로 PartialEq만 구현합니다.

7) 제네릭 코드와 동치 관계

타입 매개변수로 PartialEq만 받는 제네릭 코드를 작성할 때는 첫 번째와 두 번째 요구 조건이 지켜진다고 가정할 수 있다.
그러나 값이 그 자신과 항상 같을 거라고 가정해서는 안 된다.
만일 제네릭 코드가 완전 동치 관계를 필요로 한다면 std::cmp::Eq 트레이트를 바운드로 사용해야 한다.

8) 결론

Rust의 PartialEq 트레이트는 부분 동치 관계를 나타내며, Eq 트레이트는 완전 동치 관계를 나타낸다.
PartialEq를 구현하면 ==와 != 연산자를 사용할 수 있으며, Eq를 구현하면 완전 동치 관계를 보장할 수 있다.
Rust는 PartialEq와 Eq의 구현을 자동으로 생성할 수 있으며, 이를 통해 사용자 정의 타입에서도 상등 비교 연산을 지원할 수 있다.

04. 순서비교

Rust의 PartialOrd 트레이트는 값들 간의 부분적인 순서 비교를 가능하게 한다. 이 트레이트는 두 값이 비교 가능한 경우에만 순서 관계를 정의하며, 순서를 매길 수 없는 경우도 허용한다.

1. 순서 비교 연산자와 PartialOrd 트레이트

Rust에서 순서 비교 연산자 (<, >, <=, >=)는 std::cmp::PartialOrd 트레이트를 통해 구현된다. 이 트레이트는 상등 비교가 가능한 타입에 대해서만 순서 비교를 정의한다.

1) PartialOrd 트레이트 정의

trait PartialOrd<Rhs = Self>: PartialEq<Rhs>
where
    Rhs: ?Sized,
{
    fn partial_cmp(&self, other: &Rhs) -> Option<Ordering>;
    fn lt(&self, other: &Rhs) -> bool {
        self.partial_cmp(other) == Some(Ordering::Less)
    }
    fn le(&self, other: &Rhs) -> bool {
        matches!(self.partial_cmp(other), Some(Ordering::Less | Ordering::Equal))
    }
    fn gt(&self, other: &Rhs) -> bool {
        self.partial_cmp(other) == Some(Ordering::Greater)
    }
    fn ge(&self, other: &Rhs) -> bool {
        matches!(self.partial_cmp(other), Some(Ordering::Greater | Ordering::Equal))
    }
}

PartialOrd: 상등 비교가 가능한 타입(PartialEq)이어야 순서 비교도 가능함.
partial_cmp: 두 값을 비교하여 Option<Ordering>을 반환. 순서를 매길 수 없으면 None을 반환.
lt, le, gt, ge: partial_cmp를 사용하여 각각 <, <=, >, >= 연산자를 정의함.

PartialOrd가 Partial Eq를 확장하고 있다. 즉, 상등 비교가 가능한 타입이어야 순서 비교도 가능하다.
PartialOrd에서 직접 구현해야 하는 메서드는 partial_cmp뿐이다. partial_cmp가 Some(o)를 반환하면, o는 self와 other의 관계를 나타낸다.

2) Ordering Enum

enum Ordering {
    Less,       // self < other
    Equal,      // self == other
    Greater,    // self > other
}

3) PartialOrd 구현 예제: Interval

Interval 타입에 대해 PartialOrd를 구현하여 순서 비교를 가능하게 함.

use std::cmp::{Ordering, PartialOrd};

#[derive(Debug, PartialEq)]
struct Interval<T> {
    lower: T, // 포함
    upper: T, // 미포함
}

impl<T: PartialOrd> PartialOrd for Interval<T> {
    fn partial_cmp(&self, other: &Interval<T>) -> Option<Ordering> {
        if self == other {
            Some(Ordering::Equal)
        } else if self.lower >= other.upper {
            Some(Ordering::Greater)
        } else if self.upper <= other.lower {
            Some(Ordering::Less)
        } else {
            None
        }
    }
}

impl<T: PartialOrd> PartialOrd for Interval:
- PartialOrd 트레이트를 Interval 타입에 대해 구현.
- T는 PartialOrd 트레이트를 구현해야 함.
fn partial_cmp(&self, other: &Interval) -> Option:
- 두 Interval 값을 비교하여 순서를 반환.
- 순서를 매길 수 없는 경우(self와 other가 겹칠 경우) None을 반환.

4) PartialOrd 예제 사용

fn main() {
    let interval1 = Interval { lower: 10, upper: 20 };
    let interval2 = Interval { lower: 20, upper: 40 };
    let interval3 = Interval { lower: 7, upper: 8 };
    let interval4 = Interval { lower: 0, upper: 8 };
    let interval5 = Interval { lower: 7, upper: 1 };

    assert!(interval1 < interval2);
    assert!(interval3 > interval4);
    assert!(interval3 <= interval5);

    let left = Interval { lower: 18, upper: 30 };
    let right = Interval { lower: 28, upper: 40 };

    assert!(!(left < right));
    assert!(!(left >= right));
}

5) 순서 비교 연산자와 PartialOrd 메서드

표현식	동등한 메서드 호출	기본 정의
x < y	x.lt(y)	x.partial_cmp(&y) == Some(Ordering::Less)
x > y	x.gt(y)	x.partial_cmp(&y) == Some(Ordering::Greater)
x <= y	x.le(y)	matches!(x.partial_cmp(&y), Some(Ordering::Less
x >= y	x.ge(y)	matches!(x.partial_cmp(&y), Some(Ordering::Greater

6) 완전한 순서 비교를 위한 Ord 트레이트

Rust에서 PartialOrd 트레이트 외에도 완전한 순서 비교를 제공하는 Ord 트레이트가 있다.

7) Ord 트레이트 정의

trait Ord: Eq + PartialOrd<Self> {
    fn cmp(&self, other: &Self) -> Ordering;
}

Ord: PartialOrd를 확장하며, PartialOrd와 Eq 트레이트를 구현해야 함.
cmp: 두 값을 비교하여 항상 Ordering을 반환. 순서를 매길 수 없는 경우가 없음.

use std::cmp::Reverse;

fn main() {
    let mut intervals = vec![
        Interval { lower: 10, upper: 20 },
        Interval { lower: 5, upper: 15 },
        Interval { lower: 1, upper: 5 },
    ];

    intervals.sort_by_key(|i| i.upper);
    println!("{:?}", intervals);

    intervals.sort_by_key(|i| Reverse(i.lower));
    println!("{:?}", intervals);
}

8) 결론

PartialOrd 트레이트는 부분적인 순서 비교를 가능하게 하며, 순서를 매길 수 없는 경우를 허용한다.
Ord 트레이트는 완전한 순서 비교를 제공하며, 모든 값을 비교할 수 있다.
Interval 타입에 대해 PartialOrd와 Ord를 적절히 구현하여 순서 비교와 정렬을 지원할 수 있다.

05. Index와 IndexMut

Rust에서는 std::ops::Index와 std::ops::IndexMut 트레이트를 구현하여 a[i] 같은 색인 표현식의 동작 방식을 정의할 수 있다. 배열은 [] 연산자를 직접 지원하지만, 다른 타입에 대해서는 색인 표현식을 사용할 때 Index와 IndexMut 트레이트를 통해 메서드를 호출한다.

1. Index와 IndexMut 트레이트 정의

1) Index 트레이트

trait Index<Idx> {
    type Output: ?Sized;
    fn index(&self, index: Idx) -> &Self::Output;
}

Index: 타입 Idx를 매개변수로 받아 색인 연산을 수행하는 트레이트
type Output: 색인 연산의 결과 타입을 나타낸다.
fn index(&self, index: Idx) -> &Self::Output: 주어진 인덱스에 대한 참조를 반환하는 메서드이다.

2) IndexMut 트레이트

trait IndexMut<Idx>: Index<Idx> {
    fn index_mut(&mut self, index: Idx) -> &mut Self::Output;
}

IndexMut: Index 트레이트를 확장하여 변경 가능한 색인 연산을 지원한다.
fn index_mut(&mut self, index: Idx) -> &mut Self::Output: 주어진 인덱스에 대한 변경 가능한 참조를 반환하는 메서드이다.

2. 예제: HashMap에서의 색인 사용

use std::collections::HashMap;

let mut m = HashMap::new();
m.insert("+", 10);
m.insert("百", 100);
m.insert("千", 1000);
m.insert("万", 10_000);
m.insert("亿", 1_0000_0000);

assert_eq!(m["+"], 10);
assert_eq!(m["亿"], 1_0000_0000);

HashMap<&str, i32>는 Index<&str>를 구현하므로, m["+"]와 같은 표현식을 사용할 수 있다.
이 색인 표현식은 m.index("+")와 동등하다.

3. Index와 IndexMut의 구현 예제

use std::ops::{Index, IndexMut};

struct Image<P> {
    width: usize,
    pixels: Vec<P>,
}

impl<P: Default + Copy> Image<P> {
    fn new(width: usize, height: usize) -> Image<P> {
        Image {
            width,
            pixels: vec![P::default(); width * height],
        }
    }
}

impl<P> Index<usize> for Image<P> {
    type Output = [P];
    fn index(&self, row: usize) -> &[P] {
        let start = row * self.width;
        &self.pixels[start..start + self.width]
    }
}

impl<P> IndexMut<usize> for Image<P> {
    fn index_mut(&mut self, row: usize) -> &mut [P] {
        let start = row * self.width;
        &mut self.pixels[start..start + self.width]
    }
}

struct Image
: Image 구조체는 제네릭 타입 P를 가지며, width와 pixels 필드를 포함한다.
- width: 이미지의 너비를 나타낸다.
- pixels: 이미지의 픽셀 데이터를 저장하는 벡터이다.
impl<P: Default + Copy> Image
: new 메서드는 주어진 크기로 새 이미지를 생성한다.
impl
Index for Image
:
- Index 트레이트를 구현하여 행(row) 색인을 지원한다.
- index 메서드는 주어진 행의 픽셀 슬라이스를 반환한다.
impl
IndexMut for Image
:
- IndexMut 트레이트를 구현하여 변경 가능한 행 색인을 지원한다.
- index_mut 메서드는 주어진 행의 변경 가능한 픽셀 슬라이스를 반환한다.

4. Index와 IndexMut의 사용 예

fn main() {
    let mut desserts = vec!["Howalon".to_string(), "Soan papdi".to_string()];
    desserts[0].push_str(" (fictional)");
    desserts[1].push_str(" (real)");

    println!("{:?}", desserts);

    use std::ops::IndexMut;
    (*desserts.index_mut(0)).push_str(" (fictional)");
    (*desserts.index_mut(1)).push_str(" (real)");

    println!("{:?}", desserts);
}

desserts: 문자열 벡터입니다.
desserts[0].push_str(" (fictional)");와 desserts[1].push_str(" (real)");
- push_str 메서드는 &mut self에 작용하므로, 이 표현식들은 IndexMut 트레이트의 index_mut 메서드를 사용하여 동등한 표현으로 변환된다.

1) 주의 사항

색인 표현식이 배열, 슬라이스, 벡터 등의 범위 밖에 있는 요소에 접근하려 하면 패닉이 발생한다.
Image 예제에서 row가 범위 밖에 있으면 .index() 메서드가 self.pixels의 범위 밖을 색인하게 되어 패닉이 발생할 수 있다.

2) 결론

Index와 IndexMut 트레이트를 구현하면 사용자 정의 타입에서도 배열처럼 [] 색인 연산을 사용할 수 있다.
Index는 불변 참조를, IndexMut는 변경 가능한 참조를 반환한다.
Rust의 컬렉션 타입들은 이들 트레이트를 구현하여 색인 연산을 지원한다.
색인 연산 시 범위 밖의 요소에 접근하지 않도록 주의해야 한다.

06. 기타연산자

Rust에서 모든 연산자를 오버로딩할 수 있는 것은 아니다. 특정 연산자는 현재 오버로딩할 수 없으며, 일부는 특정 타입에만 사용할 수 있다.

1. 오버로딩이 불가능한 연산자

1) 오류 검사 연산자 `?`

설명: ? 연산자는 Result와 Option 값에만 사용할 수 있다.
현황: 사용자 정의 타입으로의 확장 작업이 진행 중

2) 논리 연산자 `&&`와 `||`

설명: 이 논리 연산자는 불(bool) 값에만 사용할 수 있다.
오버로딩 불가능: 현재는 불 값 외의 타입에 대해서는 오버로딩할 수 없다.

3) 점 연산자 `.`와 `..`

설명: . 연산자는 항상 범위의 경계를 나타내는 구조체를 생성하며, .. 연산자는 레퍼런스를 빌려오거나 값을 이동하거나 복사한다.
오버로딩 불가능: 이 연산자들은 오버로딩할 수 없다.

2. 특정 트레이트로 오버로딩 가능한 연산자

1) 역참조 연산자``

설명: val처럼 사용하는 역참조 연산자는 오버로딩할 수 있다.
사용 트레이트: Deref와 DerefMut 트레이트를 사용하여 오버로딩할 수 있다.

2) 필드 접근 및 메서드 호출 연산자 `.`

설명: val.field와 val.method()처럼 필드에 접근하고 메서드를 호출할 때 사용하는 점(.) 연산자는 오버로딩할 수 있다.
사용 트레이트: Deref와 DerefMut 트레이트를 사용하여 오버로딩할 수 있다.

3. 함수 호출 연산자 `f(x)`

설명: Rust는 함수 호출 연산자 f(x)의 오버로딩을 지원하지 않는다.
대안: 호출 가능한 값을 필요로 할 때는 클로저를 작성하면 된다.
특수 트레이트: 클로저의 동작 방식과 특수 트레이트 Fn, FnMut, FnOnce에 대해서는 14장에서 설명한다.

1) 요약

Rust에서는 모든 연산자를 오버로딩할 수 있는 것은 아니다.
? 연산자, 논리 연산자 &&와 ||, 점(.) 연산자, 그리고 & 연산자는 현재 오버로딩할 수 없다.
역참조 연산자 `와 필드 접근 및 메서드 호출 연산자 .는 Deref와 DerefMut` 트레이트를 사용하여 오버로딩할 수 있다.
함수 호출 연산자 f(x)는 오버로딩할 수 없지만, 클로저를 사용하여 대체할 수 있다.

GoldenDusk

내 지식을 기록하여, 다른 사람들과 공유하여 함께 발전하는 사람이 되고 싶다. gitbook에도 정리중 ~

이전 포스트

Rust가 떠오른 이유 : 안전성, 쾌적한 사용 - 우아한 스터디 및 잇츠 스터디

다음 포스트

Chater 12. 연산자 오버로딩

Rust

Chater 12. 연산자 오버로딩

01. 도입

1. 연산자 오버로딩(operator overloading)이란?

2. 연산자 오버로딩을 위한 트레이트

02. 산술 연산자와 비트별 연산자

1. add의 표현식

1) std::ops :: Add

2) std::ops::Add 트레이트 정의

3) 복소수 타입 Complex의 Add 트레이트 구현

4) 다양한 Complex 타입에 대해 제네릭으로 Add 트레이트 구현

5) 더욱 일반적인 제네릭 구현

6) 실제로 Rust에서의 제약

7) 결론

2. 단항 연산자

1) 단항 연산자를 위한 기본 제공 트레이트

2) 트레이트 정의

3) 복소수의 부호 부정 구현

4) 결론

3. 이항 연산자

1) 이항 연산자를 위한 기본 제공 트레이트 : 산술 연산자

2) 이항 연산자를 위한 기본 제공 트레이트 : 비트별 연산자

3) 기본 제공 트레이트의 일반적인 형태

4) Rust의 수치 및 비트 연산자

5) 문자열 연결에 대한 특이 사항

4. 복합 배정 연산자

1) 복합 배정 연산자란?

2) 복합 배정 연산자를 위한 기본 제공 트레이트

3) Rust의 수치 타입과 정수 타입

4) Complex 타입에 대한 AddAssign 트레이트 구현

설명:

5) 복합 배정 연산자 트레이트와 이항 연산자 트레이트의 관계

6) 결론

03. 동치비교

1. PartialEq

1) std::cmp::PartialEq의 정의

2) PartialEq 구현 예시 : Complex을 위한 완전한 구현

3) PartialEq 구현의 자동 생성

4) PartialEq와 Eq의 관계

2. 산술과 비트별 트레이트와 PartialEq

1) 산술과 비트별 트레이트와 PartialEq의 차이

2) 산술과 비트별 트레이트와 PartialEq의 차이 예제 코드

3) PartialEq 트레이트의 Rhs 타입 매개변수 : Rhs 타입 매개변수의 트레이트 바운드

4) PartialEq의 사용 예

3. 동치 관계와 부분 동치 관계

1) 동치 관계의 수학적 정의

2) IEEE 표준 부동소수점 값과 NaN

3) 부분 동치 관계 (Partial Equivalence Relation)

4) 완전 동치 관계 (Full Equivalence Relation)

5) PartialEq의 구현 예

5) Eq의 구현 예

6) 자동 생성

7) 제네릭 코드와 동치 관계

8) 결론

04. 순서비교

1. 순서 비교 연산자와 PartialOrd 트레이트

1) PartialOrd 트레이트 정의

2) Ordering Enum

3) PartialOrd 구현 예제: Interval

4) PartialOrd 예제 사용

5) 순서 비교 연산자와 PartialOrd 메서드

6) 완전한 순서 비교를 위한 Ord 트레이트

7) Ord 트레이트 정의

8) 결론

05. Index와 IndexMut

1. Index와 IndexMut 트레이트 정의

1) Index 트레이트

2) IndexMut 트레이트

2. 예제: HashMap에서의 색인 사용

3. Index와 IndexMut의 구현 예제

4. Index와 IndexMut의 사용 예

1) 주의 사항

2) 결론

06. 기타연산자

1. 오버로딩이 불가능한 연산자

1) 오류 검사 연산자 ?

2) 논리 연산자 &&와 ||

3) 점 연산자 .와 ..

2. 특정 트레이트로 오버로딩 가능한 연산자

2) `std::ops::Add` 트레이트 정의

4) 다양한 `Complex` 타입에 대해 제네릭으로 Add 트레이트 구현

4) `Complex` 타입에 대한 `AddAssign` 트레이트 구현

1) 오류 검사 연산자 `?`

2) 논리 연산자 `&&`와 `||`

3) 점 연산자 `.`와 `..`

2) 필드 접근 및 메서드 호출 연산자 `.`

3. 함수 호출 연산자 `f(x)`