
💫 비선형 구조란 일렬로 나열하지 않고 자료구조나 관계가 복잡한 구조를 말한다.
그래프
🍐 개념
- 노드(정점)와 간선으로 표현
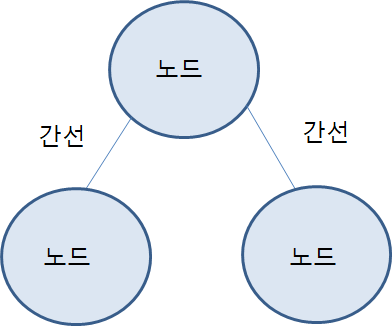
정점과 간선
어떠한 곳에서 어떠한 곳으로 무언가를 통해 간다고 했을 때
- 정점 : 어떠한 곳, 출발지와 도착지
- 간선 : 무언가가 되며, 가는 길
단방향 간선
- 짝사랑 : 일방적 간선
- 사랑 : 양방향 간선
🍐 그래프의 기본구조
- 그래프 탐색이란? 하나의 노드를 시작으로 다수의 노드에 방문하는 것
- 두 노드는
인접하다= 두 노드가 간선으로 연결되어 있다
🍐 용어
8/23 국비에서 배운 내용 추가
- 노드 (Node): 위치, 정점(Vertex)
- 간선 (Edge): 위치 간의 관계를 표시한 선. 노드를 연결한 선(link 또는 branch)
- 인접 정점 (Adjacent Vertex) : 간선으로 직접 연결된 정점(또는 노드)
- 정점의 차수 (Degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수 (In-Degree): 방향 그래프에서 외부에서 오는 간선의 수
- 진출 차수 (Out-Degree): 방향 그래프에서 외부로 향하는 간선의 수
- 경로 길이 (Path Length): 경로를 구성하기 위해 사용된 간선의 수
- 단순 경로 (Simple Path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
- 사이클 (Cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
🍐 그래프의 표현법 2가지
1. 인접 행렬(Adjacency Matrix) : 2차원 배열로 연결 관계를 표현하는 방식
- 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식
2차원 리스트- 연결되어 있지 않은 노드끼리 무한의 비용이라고 작성
- 장점
- 속도 측면 : 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 인접 리스트보다 빠르다 ⇒ 그래프 내의 노드 간 관계를 상수 시간(O(1))에 확인 가능 ⇒ 이유 : 모든 관계를 저장하고 있으니까
- 간선의 유무와 가중치를 저장하기에 유용
- 이유 : 모든 관계 저장하니까
- 작은 밀집 그래프에서 메모리 더 효율적 사용 가능
- 메모리 오버헤드가 작음: 작은 그래프의 경우 인접 행렬은 노드 수에 비해 상대적으로 적은 메모리를 사용
- 간선 개수가 상대적으로 많음:
밀집 그래프는 간선이 노드 수에 비해 많이 존재하는 경우를 가리킨다. 인접 리스트는 각 노드마다 연결된 노드의 리스트를 유지해야 하므로, 간선이 많은 경우에는 이 리스트들의 크기가 커져서 메모리 사용이 증가함 이와 달리 인접 행렬은 간선의 유무만 표시하면 되기 때문에 간선의 개수와는 무관하게 메모리 사용량이 일정 - 빠른 간선 조회: 인접 행렬은 간선의 유무를 상수 시간(O(1))에 확인할 수 있다. 작은 밀집 그래프에서는 이런 간선 조회가 더 효율적
- 단점
- 메모리 측면 : 모든 관계를 저장하므로 노드 개수가 많을수록 메모리 낭비
INF = 999999999 # 무한의 비용 선언(연결되어 있지 않은 노드)
# 2차원 히스트를 이용해 인접한 행렬 표현
graph = [
[0, 7, 5],
[7, 0, INF],
[5, INF, 0]
]
print(graph)[결과창]

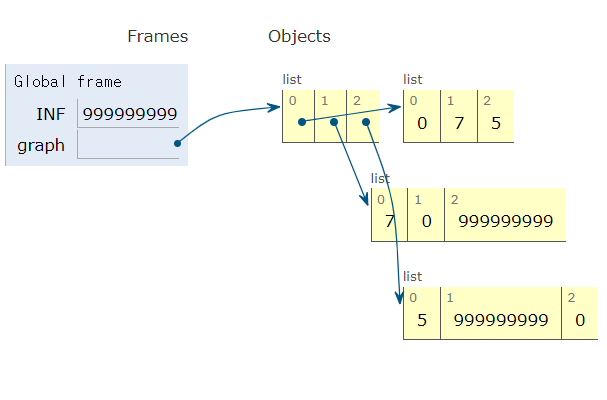
2. 인접 리스트(Adjacency List) : 리스트로 그래프의 연결 관계를 표현하는 방식
- C++ Java의 경우, 별도의 연결 리스트 기능을 위한 표준 라이브러리 제공
- 파이썬의 경우 기본 자료형인 리스트 자료형이
append()와 메소드 제공 ⇒ 배열과 연결 리스트의 기능을 모두 기본으로 제공
- 연결 리스트를 이용해 그래프를 표현하고자 할 때에도
2차원 리스트이용하면 됨
- 장점
- 메모리 측면 : 연결된 정보[노드]만을 저장하기 때문에 인접행렬방식보다 효율적
- 그래프의 크기나 노드 수에 무관하게 상대적으로 작은 메모리를 사용
- 그래프 탐색 시 연결된 노드 빠르게 순회 가능
- 희소 그래프에서 적합함
희소 그래프란 그래프 내에 간선의 수가 상대적으로 적은 경우- 메모리 절약: 인접 리스트는 각 노드마다 연결된 노드들을 저장하기 때문에, 연결되지 않은 노드 사이에는 공간이 낭비되지 않음
- 빠른 간선 조회: 인접 리스트는 노드마다 연결된 노드들을 순회하므로 연결된 노드들에 대한 조회가 빠르게 이루어진다. 희소 그래프에서는 노드 간의 연결이 적어서 인접 리스트로 연결된 노드를 빠르게 조회 가능
- 시간 복잡도 개선: 인접 리스트를 사용하면 희소 그래프에서 그래프 탐색 알고리즘의 시간 복잡도를 개선할 수 있다. 노드 간의 관계가 적어서 탐색을 중지하는 경우가 더 많기 때문
- 단점
- 속도 측면 : 연결된 데이터를 하나씩 확인해야 하기 때문에 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.
- 예제
- 해석
graph[0]에 저장된 정보 : 노드 0과 연결된 노드 1, 거리 7 + 노드 0과 연결된 노드 2, 거리 5graph[1]에 저장된 정보 : 노드 1과 연결된 노드 0 저장graph[2]에 저장된 정보 : 노드 2와 연결된 노드 0만이 저장
# 행(Row)이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(연결된 노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))
# 노드 1에 연결된 노드 정보 저장
graph[1].append((0, 7))
# 노드 2에 연결된 노드 정보 저장
graph[2].append((0, 5))
print(graph)- 코드 시각화 사진
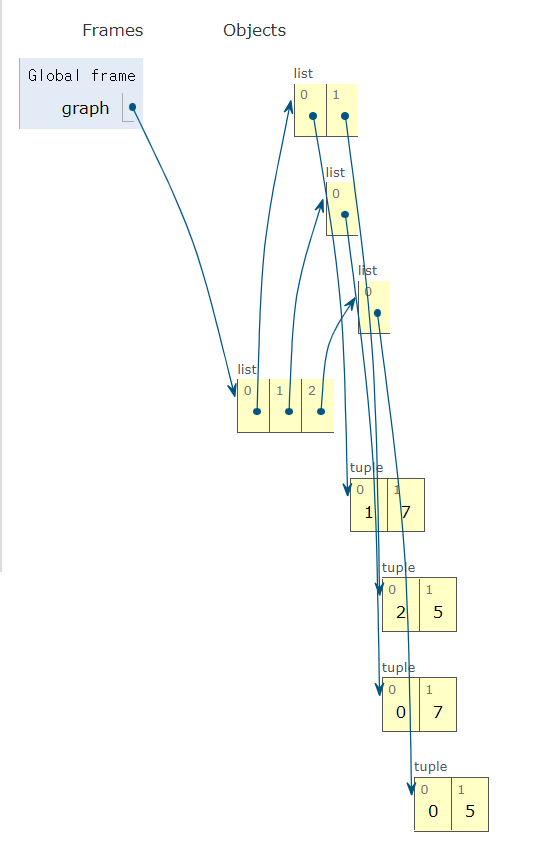
[결과창]

🍐 그래프 (Graph) 종류
무방향 그래프 (Undirected Graph)
- 방향이 없는 그래프
- 간선을 통해, 노드는 양방향으로 갈 수 있음
방향 그래프 (Directed Graph)
- 간선에 방향이 있는 그래프
가중치 그래프 (Weighted Graph) 또는 네트워크 (Network)
- 간선에 비용 또는 가중치가 할당된 그래프
연결 그래프 (Connected Graph)
- 무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우
비연결 그래프 (Disconnected Graph)
- 무방향 그래프에서 특정 노드에 대해 경로가 존재하지 않는 경우
사이클 (Cycle)
- 단순 경로의 시작 노드와 종료 노드가 동일한 경우
비순환 그래프 (Acyclic Graph)
- 사이클이 없는 그래프
완전 그래프 (Complete Graph)
- 그래프의 모든 노드가 서로 연결되어 있는 그래프
🍐 그래서 어디서 쓰냐?[chat gpt의 답변]
즉, 그래프는 깊이 우선 탐색과 너비 우선 탐색을 하기 위한 목적
- 최단 경로 알고리즘: 두 노드 사이의 최단 경로를 찾는 알고리즘으로, 다익스트라 알고리즘, 벨만-포드 알고리즘 등이 포함됩니다.
- 신장 트리 알고리즘: 그래프 내의 모든 노드를 포함하는 트리 구조를 생성하는 알고리즘으로, 프림 알고리즘과 크루스칼 알고리즘이 포함됩니다.
- 흐름 네트워크 알고리즘: 네트워크의 흐름을 최적으로 관리하는 알고리즘으로, 포드-풀커슨 알고리즘이 대표적입니다.
- 그래프 탐색 알고리즘: 그래프 내의 모든 노드를 탐색하는 알고리즘으로, 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 포함됩니다.
- 위상 정렬 알고리즘: 방향 그래프에서 순서가 있는 작업을 정렬하는 알고리즘입니다.
- 최소 신장 트리 알고리즘: 가중치가 있는 그래프에서 모든 노드를 포함하는 신장 트리 중 가중치의 합이 최소인 트리를 찾는 알고리즘으로, 프림 알고리즘과 크루스칼 알고리즘이 있습니다.
- 경로 찾기 알고리즘: 두 노드 간의 경로를 찾는 알고리즘으로, 깊이 우선 탐색(DFS)이나 너비 우선 탐색(BFS)을 활용하여 구현될수 있습니다.
- 네트워크 플로우 알고리즘: 특정 조건하에서 네트워크 내에서 정보나 물량의 흐름을 최적으로 관리하는 알고리즘입니다.
