[python] OOP 및 자료구조(배열/ 스택/ 큐/ 연결리스트/ 트리/ 그래프)

📌 4일차 배운 내용 목차

번호	주제	세부 내용
1	객체 지향 프로그래밍 (OOP)	-
2	사용자 정의 자료형 : VO	-
3	예외 처리 방법	-
4	자료구조(1) 선형 자료구조	배열, 연결리스트, 스택, 큐
5	자료구조(2) 비선형 자료구조	트리, 그래프

---

✏️1. 객체 지향 프로그래밍 (OOP)

1.1 OOP정의 및 사용이유

what❓객체 지향 프로그래밍

: 현실 세계를 객체(Object)로 모델링하여, 객체 간의 상호작용을 통해 프로그램을 구성하는 방식의 프로그래밍 패러다임

why❓ 사용

1) 코드의 재사용성 : 한번 만든 클래스는 여럭 객체에서 재사용 가능
2) 유지보수 용이성 : 기능별로 객체가 나눠져 있어서 수정이나 확장이 쉬움
3) 캡슐화: 내부 구현을 감추고, 외부에는 필요한 인터페이스만 제공!
4) 추상화 : 복잡한 로직을 숨기고 필요한 기능만 표현
5) 상속성과 다형성 :

• 기존 클래스의 기능을 물려 받아 새기능 추가 (상속)
• 같은 메서드 이름으로 다양한 행동 정의(다형성)

객체(object) : 추상적, 구체적인 개념 + 수학 함수 / /독립적 단위
클래스(Class) : 객체를 만들기 위한 설계도
인스턴스(instance) : 클래스로부터 만들어진 실체화(메모리에 올라감)된 객체

---

1.2 객체 지향 프로그램의 4가지 특징

개념	설명	파이썬 관련 참고
추상화	복잡한 시스템에서 핵심 정보만 보여주고, 불필요한 정보는 감춤 (객체의 대표적인 특징을 추출하는 행위)	-
상속	기존 클래스의 속성과 기능을 새로운 클래스가 물려받아 재사용 (자식 클래스가 부모 클래스의 멤버를 상속)	-
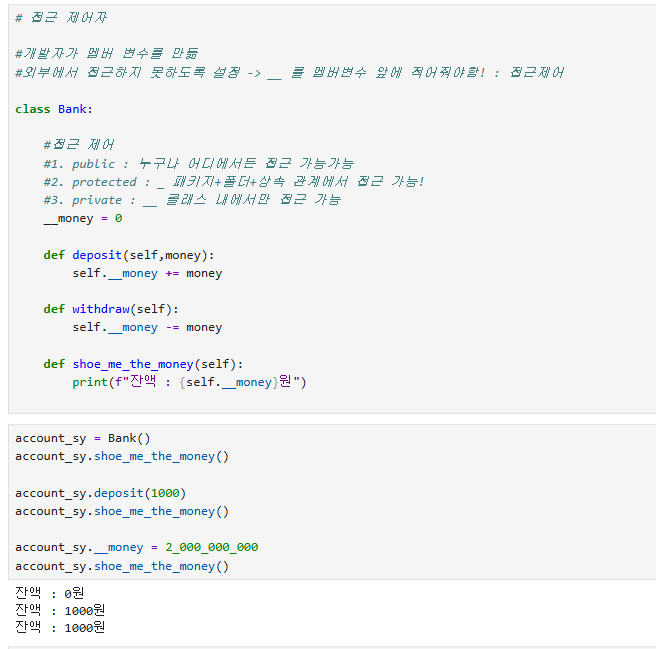
캡슐화	데이터와 기능을 하나로 묶고, 외부에서 직접 접근하지 못하도록 제한	# __private: 클래스 내 # _protected: 패키지, 상속 # public: 어디든
다형성	같은 메서드 이름이지만, 객체에 따라 다르게 동작	# override: 자식 클래스에서 부모 클래스 함수 재정의

🚨약속!

1) 클래스명 은 대문자로 시작!
2) 첫번째 매개변수는 반드시 self!!

str 함수

: 정해진 약속 인스턴스 이름을 부르면 동작하는

✏️예제코드

1) 저금통 클래스
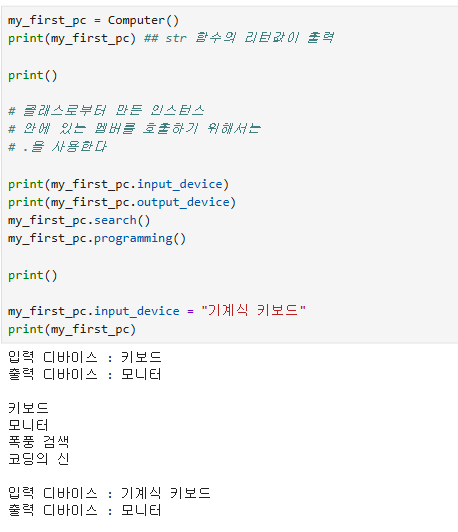
2)컴퓨터 클래스

---

✏️2. VO(value object) 사용자 정의 자료형

2.1 VO 정의

What? VO

• 예를 들어 이름은 문자열, 나이는 정수, 주소는 문자열인 구조가 필요할 때, 파이썬에 그런 자료형이 미리 정의되어 있는 건 없으니, 클래스를 만들어 직접 정의하자! 이런 식으로 만든 클래스가 바로 VO(Value Object)
  
  
  

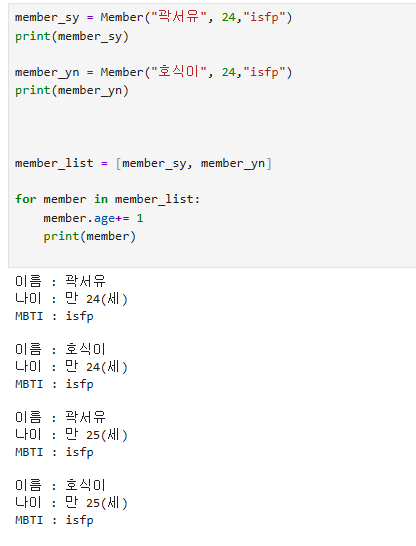
✏️예제코드

2.2 접근제어자

접근 제어자? :

• 클래스 내부 정보를 보호하고, 외부에서의 잘못된 접근을 막기 위한 장치
• 파이썬에서는 __변수명 같은 네이밍 규칙으로 이를 표현함.
  
  
  

✏️예제코드

---

✏️3. 예외 처리

에러 클래스를 통해 특정에러 상황 발생시 , 사용자에게 스크립트 제공 + 에러라인 제공

• try ~except + (finally) 구문사용!
  
  
  
  

  ✏️예제코드

---

✏️4. 자료구조(1) 선형 자료구조

4.1 배열 구현

파이썬에서 배열 특징

• 인덱스를 통해 데이터에 빠르게 접근 가능
• 크기 고정
• 파이썬에서는 list를 array처럼 사용!
• insert(요소) -> 값추가! 가장 마지막에
• get (index) -> 해당 인덱스의 값을 리턴
• 인스턴스 이름 자체를 호촐 -> 모든 값 출력!

✏️예제코드

class Array:

	def __init__(self): 
        self.data = []
        
	def insert(self, value):
        self.data.append(value)
        
    def get(self, index):
        return self.data[index]
        
    def __str__(self):
        return str(self.data)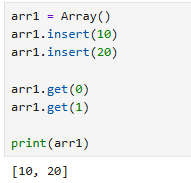

4.2 Stack(스택) 구현

스택?

:FILO : First in! Last out! ( last in first out) // 위로 쌓고 위에서 빼는

Stack class에 필요한 함수

1. push(value)
2. pop() -> 가장 위(마지막 요소) 꺼내고 ! 리턴까지!
3. peek() -> 마지막 요소 리턴, 없다면 -1 리턴
4. is_empty() -> 비어 있으면1, 아니면 0

✏️예제코드

class Stack:

    def __init__(self):
        self.stack = []
        
    def push(self,value):
        self.stack.append(value)
        
    def pop(self):    
            temp = self.stack[-1]
            del self.stack[-1]
            return temp
            
        #2번째 방법
        # 파이썬에서 리스트에 자체적으로 pop() 함수가 존재
        # self.stack.pop()
        
    def peak(self):    
        return -1 if self.is_empty()==1 else self.stack[-1]
        
    def is_empty(self):
        if len(self.stack) ==0 :
            return 1
        else:
            return 0

#함수 매개변수 : 데이터 타임
# 타입 체크 가능
# def 함수명(매개변수 :데이터타입) -> 리턴타입
def is_valid(quiz : str )-> bool:    

    stack = Stack()
    is_correct = True
    
    for p in quiz:
        if p == "(":
            stack.push("(")
        else:
            if stack.is_empty() == 1:
                is_correct = False
                break
            else:
                if stack.pop() == "(":
                    continue
                else:
                    is_correct = False
                    break
                    
    return is_correct and stack.is_empty() ==1            

4.3 Queue (큐) 구현

큐?

:FIFO : first in last out 선입선출!빼는

Queue class에 필요한 함수

1. enqueue(value)
2. dequeue()
3. is_empty() -> 비어 있으면1, 아니면 0

✏️예제코드

from collections import deque

class My_Queue:

    def __init__(self):
        self.deque = deque()
        
    def enqueue(self, value):
        self.queue.append(value)
        
    def dequeue(self):
        return self.queue.popleft()
        
    def is_empty(self):       
        if len(self.queue) == 0:
            return 1
        else:
            return 0
            

# 파이썬에서 라이브러리로 구현
q = deque()
q.append(10)
q.append(20)
print(q.popleft())
print(q.popleft())

4.4 Linked list(연결 리스트) 구현

연결리스트?

: 노드간 연결구조
-> 큐 구현 ( C에선 구조체, 파이썬에선 연결리스트)
: 삽입/삭제가 빠르다

✏️예제코드

• 1->3->7->11
• 현재 value, 다음값의 주소를 가지고 있어야
  
  
  

class Node:
    def __init__(self, value):
        self.value = value
        self.next = None # 아직은 모름
        # value 1
        # next non
        # value 3
        # 이 순간 1의 next가 3을 가리켜야 함
        # 3의 next : None

class Linked_List:

    def __init__(self):
        self.head = None # 그냥헤드  
        
    def appened(self, value):
        new_node = Node(value) #재귀의 느낌~
        if not self.head : # 헤드가 none이면 통과
            self.head = new_node
            return
            
        curr = self.head        
        while curr.next:
            curr = curr.next
        curr.next = new_node   
        
    def display(self):
    
        curr = self.head
        
        while curr:
            print(f"{curr.value} -> ", end="")
            curr = curr.next
        print("None")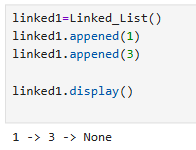

✏️ 백준 큐2 문제

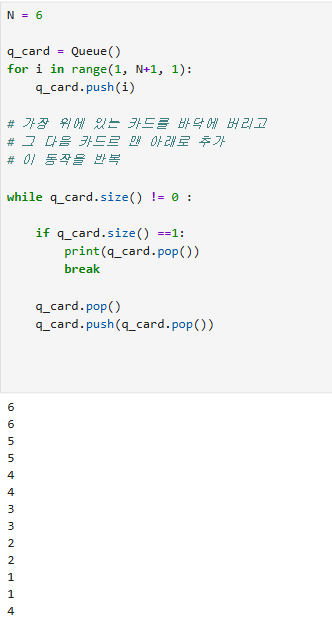
class Queue:
    def __init__(self):
        self.queue =[]
        
    def push(self, value):
        self.queue.append(value)    
        
    def pop(self):
        #큐에 들어 있는 정수가 있는 경우
        if len(self.queue) != 0:            
            temp = self.queue[0]
            del self.queue[0]
            return temp
        else:
            print(-1)
            return -1       
            
    def size(self):
        print(len(self.queue))
        return len(self.queue)       
        
    def empty(self):
        print( 1 if len(self.queue) ==0 else 0 )
        return len(self.queue) ==0
        
    def front(self):
        print(self.queue[0] if self.empty == 0 else -1)
        
    def back(self):
        print(self.qeue[-1] if self.empty == 0 else -1)

---

✏️5. 자료구조(2) 비선형 자료구조

5.1 트리 구현

5.1.1 트리란? 트리사용이유?

✏️What? 트리

• 데이터를 계층 구조로 표현하고, 부모-자식 관계를 기반으로 효율적인 검색/정렬/구조 표현이 가능한 자료구조

​

​

✏️Why? 사용

• 트리는 주로 계층 구조를 갖는 데이터를 저장하고 관리하기 위해 사용됨
• 예를 들어, 파일 시스템의 폴더 구조, 조직도, 계층적인 디렉토리 구조 등이 트리 자료구조를 이용하여 표현
• 또한 검색 트리(search tree)라는 특별한 종류의 트리 자료구조를 이용하여 데이터를 저장하고 검색할 수 있음 // 검색 트리의 예로 이진 검색 트리(binary search tree)가 있음
  ​

​

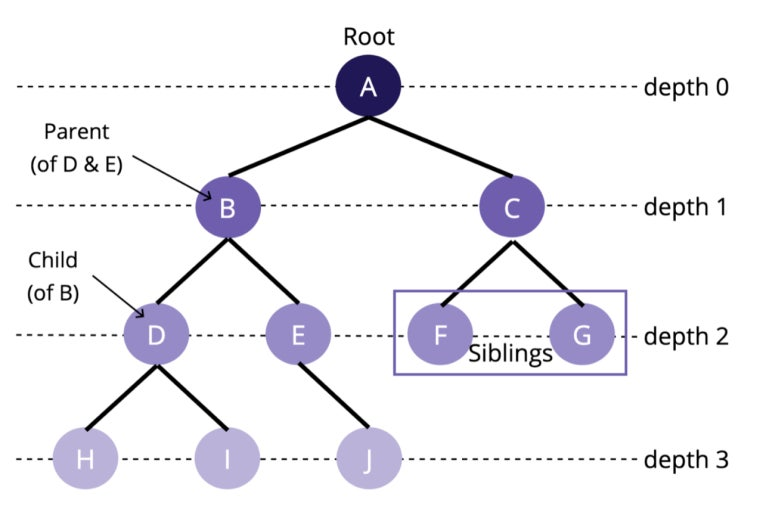
✏️트리 구조

• 일반적으로 루트(root) 노드가 존재하고 각 노드는 하나 이상의 자식(child) 노드를 가질 수 있음
• 자식 노드는 부모(parent) 노드로부터 상속받은 속성을 갖는 경우가 많음
• 부모-자식 계층구조

​

​

✏️트리의 종류

5.1.2 트리 클래스 구현 및 만들기

트리클래스

class Tree:
    def __init__(self,value):
        self.value = value
        self.left = None
        self.right = None

트리만들기

#백준 1991번 문제

tree_A = Tree("A")
tree_B = Tree("B")
tree_C = Tree("C")
tree_D = Tree("D")
tree_E = Tree("E")
tree_F = Tree("F")
tree_G = Tree("G")

tree_A.left = tree_B
tree_A.right = tree_C
tree_B.left = tree_D
tree_C.left = tree_E
tree_C.right = tree_F
tree_F.right = tree_G

전위순회 / 중위순회 / 후위순회

# 1.전위 순회한 결과
#"ABCDEFG"

def pre_order(tree):
    if tree:
        print(tree.value, end="")
        # 자기 자신을 참조하는 재귀함수!
        pre_order(tree.left)
        pre_order(tree.right)

pre_order(tree_A)
print()

#2. 중위 순회
def in_order(tree):
    if tree:
        in_order(tree.left)
        print(tree.value, end = "")
        in_order(tree.right)

in_order(tree_A)
print()


#3. 후위 순위
def post_order(tree):
    if tree:
        post_order(tree.left)
        post_order(tree.right)
        print(tree.value, end = "")

post_order(tree_A)
print()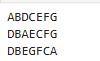

5.2 그래프 구현

5.2.1 그래프란? 그래프 사용이유?

What? 그래프

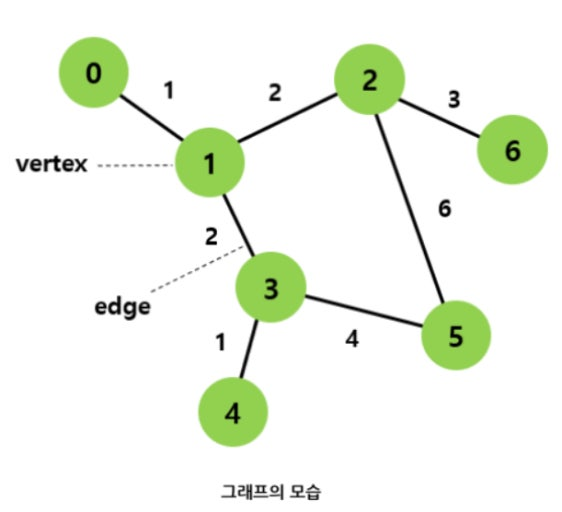
• 정점(노드)과 간선(연결선)으로 구성된 비선형 자료구조로, 객체 간의 복잡한 관계나 연결 구조를 표현할 수 있는 구조

​

​

Why? 그래프

그래프의 구조

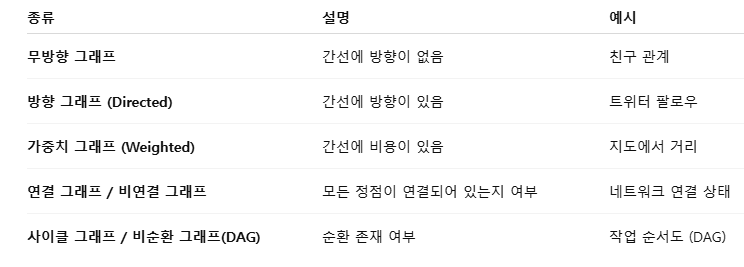
그래프의 종류

5.2.2 그래프 클래스 구현 및 만들기

그래프 클래스 만들기

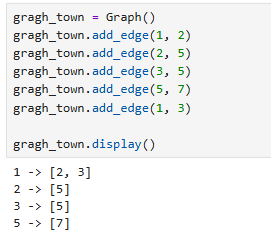
• 1 -> [2, 3]
• 2 -> [5]
• 3 -> [5]
• 5 -> [7]

class Graph:

    def __init__(self):
        self.graph = {}



    def add_edge(self, u, v):
        if u not in self.graph:
            # 해당 key 가 없으면
            # 빈 리스트를 value로

            self.graph[u] = []

        self.graph[u].append(v)


    def display(self):
        # {1:[2, 3], 2:[5], 3:[5], 5:[7]}
        for g in self.graph:
            print(f"{g} -> {self.graph[g]}")

그래프 만들기

5.3 그래프 트리 차이점