Algorithm | 3. 투포인터

완전탐색으로 해결하면 시간초과가 나는 경우가 있는데, 이 때 투포인터 알고리즘으로 해결을 해야하는 경우가 다수이다.

1차원 배열에서 2개의 포인터를 조작하는 방식

조건

1. left, right 포인터 2개
2. 처음 포인터는 left = 0, right = 0
3. left <= right

여기서 중요한 것은 [left, right) 라는 것이다. 따라서 left = right이면 크기가 0인 배열이다.

알고리즘

부분합이 M인 경우를 찾는다고 해보자.
1. 부분합이 M보다 클 경우, left 1 증가
2. 부분합이 M보다 작을 경우, right 1 증가
3. 부분합이 M일 경우, count -> left 1 증가

left가 이동하는 경우는

• 부분합이 M보다 클 경우
• 부분합이 M일 경우
• right가 가장 마지막 index에 위치할 경우

초기상태

1. left = 0, right = 0
2. sum = 0
3. M = 21
4. count = 0

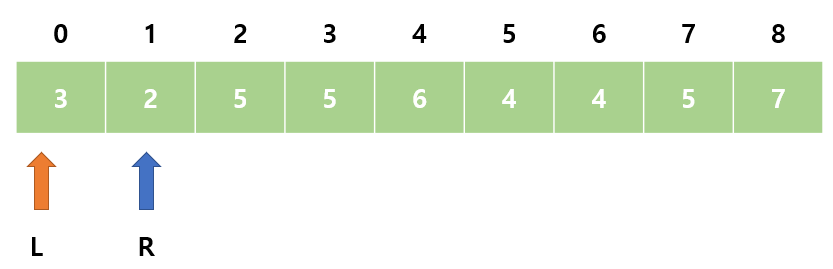
1. 초기상태는 L = 0, R = 0 이다. sum = 0 이므로 R을 오른쪽으로 이동한다.

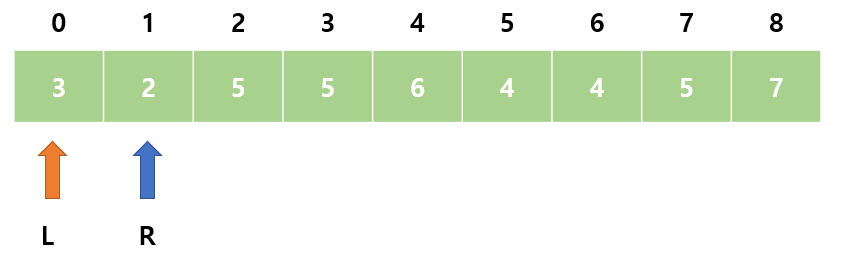
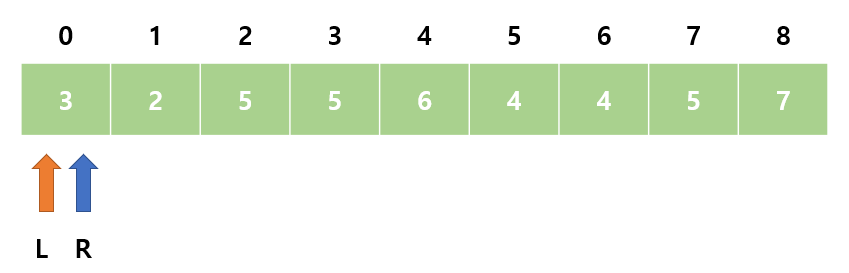
2. sum = 3으로 M보다 작다. R을 오른쪽으로 이동한다.

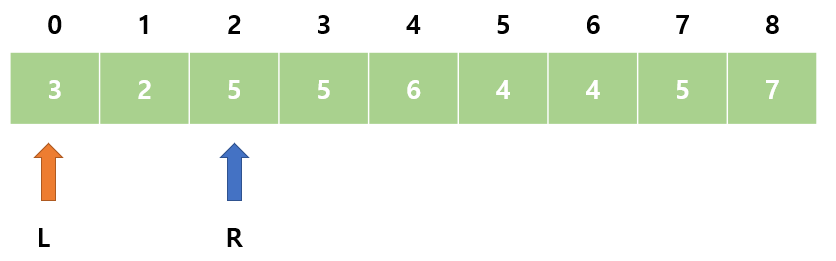
3. sum = 5으로 M보다 작다. R을 오른쪽으로 이동한다.

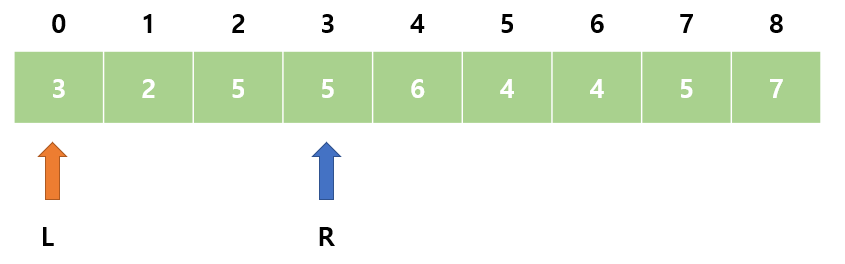
4. sum = 10으로 M보다 작다. R을 오른쪽으로 이동한다.

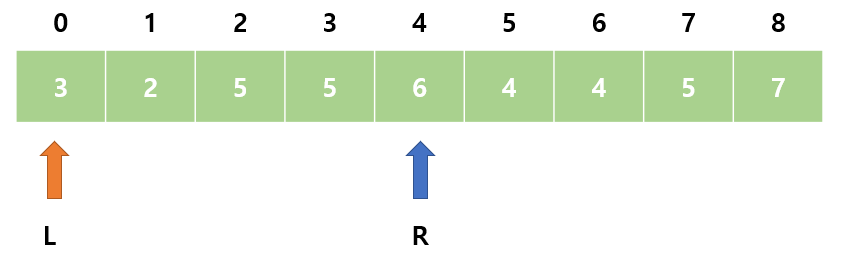
5. sum = 15으로 M보다 작다. R을 오른쪽으로 이동한다.

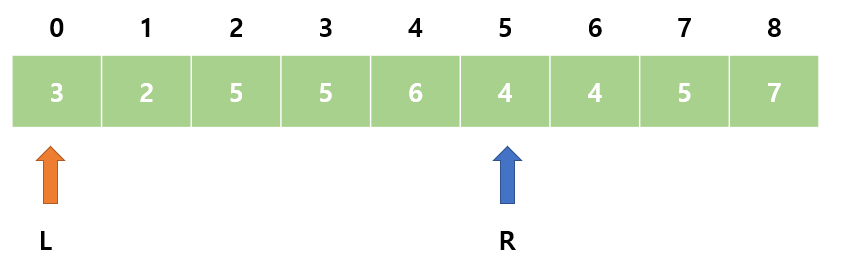
6. sum = 21으로 M과 같다. count = 1 이다. L을 오른쪽으로 이동한다.

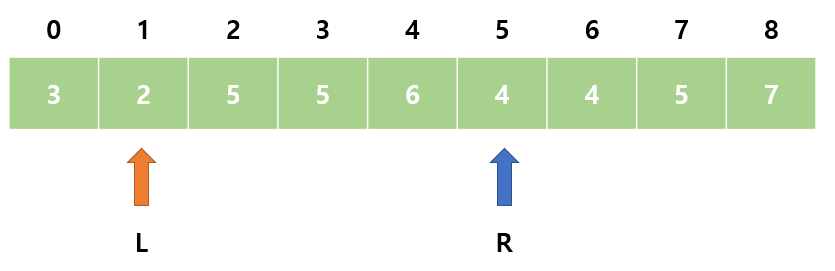
7. sum = 19으로 M보다 작다. R을 오른쪽으로 이동한다.

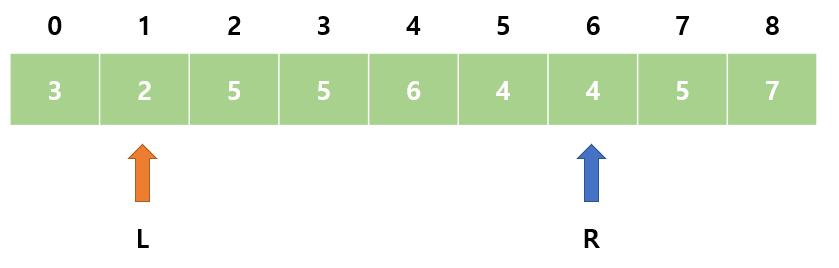
8. sum = 22으로 M보다 크다. L을 오른쪽으로 이동한다.

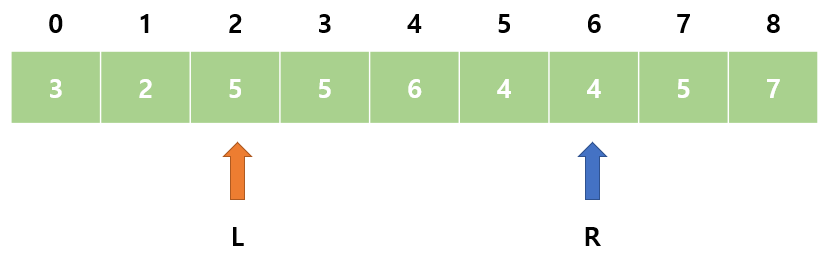
9. sum = 20으로 M보다 작다. R을 오른쪽으로 이동한다.

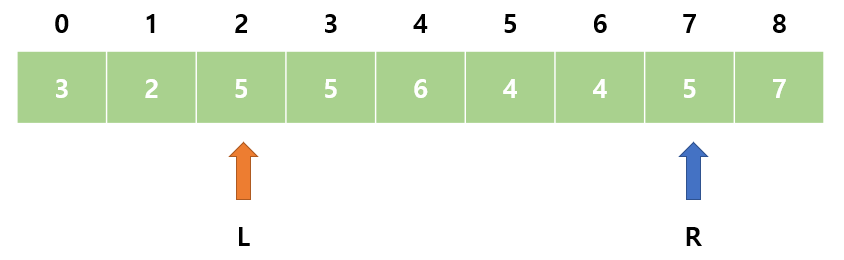
10. sum = 24으로 M보다 크다. L을 오른쪽으로 이동한다.

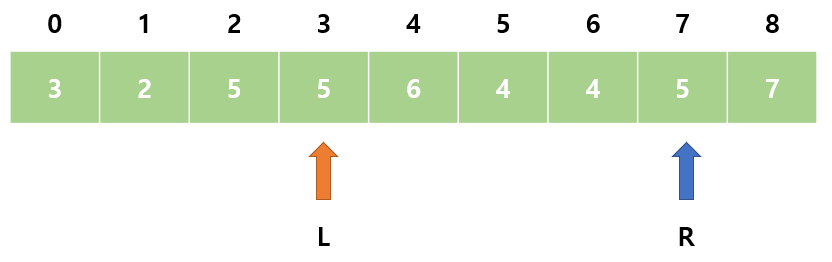
11. sum = 19으로 M보다 작다. R을 오른쪽으로 이동한다.

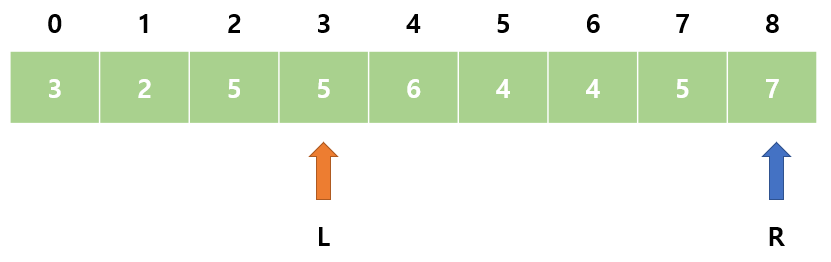
12. sum = 24으로 M보다 크다. L을 오른쪽으로 이동한다.

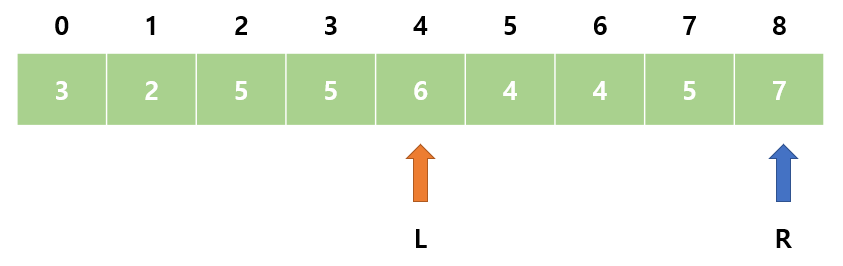
13. sum = 19으로 M보다 작다. R이 이미 제일 끝에 위치하므로 L을 오른쪽으로 이동한다.

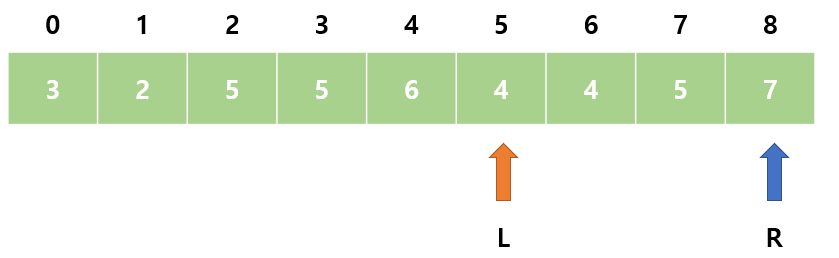
14. sum = 11으로 M보다 작다. R이 이미 제일 끝에 위치하므로 L을 오른쪽으로 이동한다.

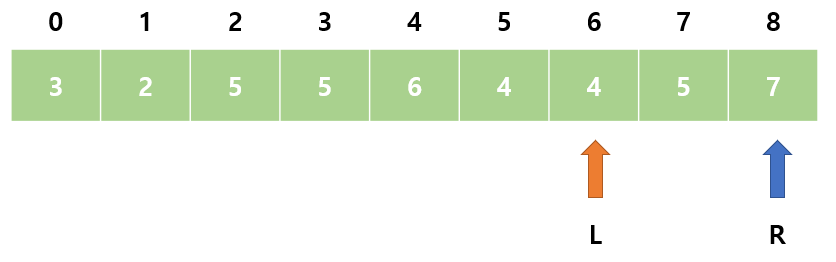
15. sum = 9으로 M보다 작다. R이 이미 제일 끝에 위치하므로 L을 오른쪽으로 이동한다.

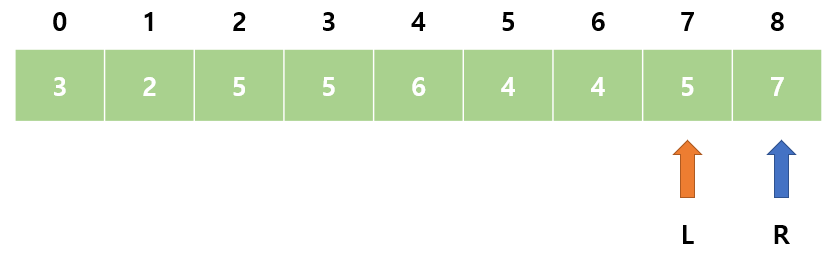
16. sum = 5으로 M보다 작다. R이 이미 제일 끝에 위치하므로 L을 오른쪽으로 이동한다.

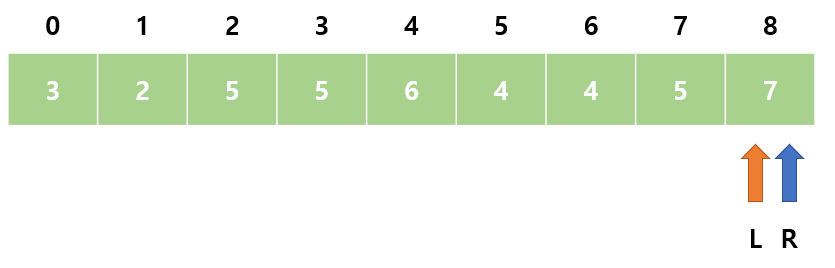
17. sum = 0으로 M보다 작다.

코드

n = 9 # 데이터의 개수 N
m = 21 # 찾고자 하는 부분합 M
data = [3, 2, 5, 5, 6, 4, 4, 5, 7] # 전체 수열

count = 0
interval_sum = 0
right = 0

# left를 차례대로 증가시키며 반복
for left in range(n):
    while interval_sum < m and end < n:
        interval_sum += data[right]
        right += 1
    # left가 이동하는 구간
    # 부분합이 m보다 크거나 같을 경우
    if interval_sum == m:
        count += 1
    interval_sum -= data[left] # 합에서 제외하고 -> for문에서 오른쪽으로 이동
    
print(count)

어려웠던 점

right부분이 열린구간인 점을 간과한 점이 제일 큰 오류였다. 이 부분 때문에 다른 사람의 코드를 봐도 이해가 안된듯..!!ㅠ
이전 구간의 합을 확인한 후 -> 이동해도 됨? 판단하는 로직이었다. 순서 뒤 바뀌면 안돼~