모든 C언어 코드들은 정상 구현됩니다!
포스팅을 읽기에 앞서... 굉장히 구현하기도 이해하기도 까다로운 트리라고 생각됩니다. 그래서 해당 포스팅 내용이 완벽하다곤 생각하지 않습니다. 참고하여 주시고 읽어주시면 감사드리겠습니다.
수정해야될 부분이 있다면 계속 수정할 예정입니다.
[참고 사이트]
https://velog.io/@kku64r/rbtree
https://namu.wiki/w/%EB%A0%88%EB%93%9C-%EB%B8%94%EB%9E%99%20%ED%8A%B8%EB%A6%AC
https://blogshine.tistory.com/102
https://dev-game-standalone.tistory.com/92
회전관련: https://velog.io/@prkty/AVL-%ED%8A%B8%EB%A6%AC-vjg219mw
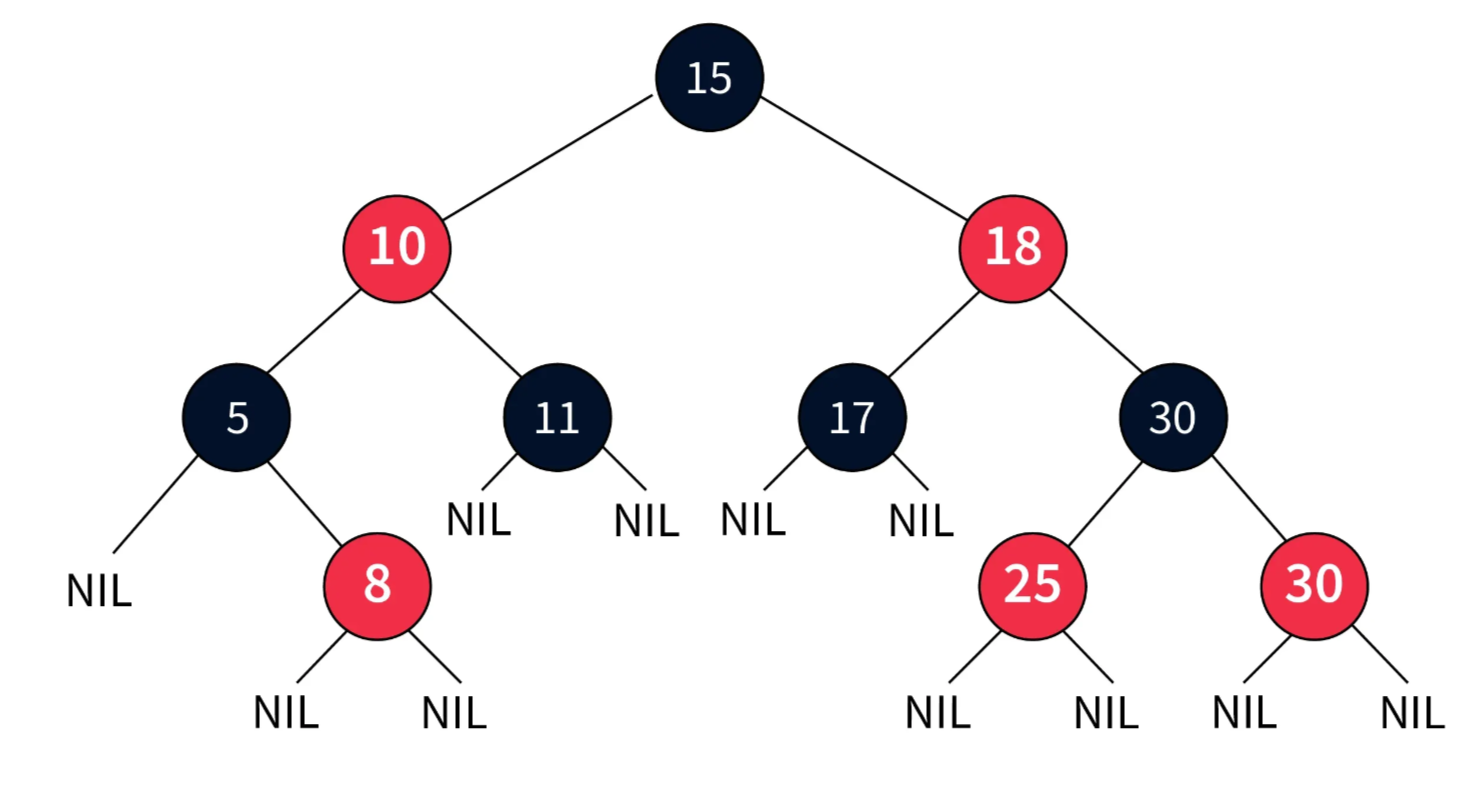
RB Tree
RB 트리는 이진트리에서 자식들이 한쪽으로 치우치는 것을 막기 위한 균형기능이 들어간 자가 균형 이진 트리이다. 자가 균형 이진트리는 대표적으로 전에 배웠던 자식의 Depth를 이용하는 AVL 트리와, 노드의 색을 이용하는 Red Black Tree 등이 있다.
시간복잡도
이진 탐색 트리의 경우 균형이 맞지 않으면, 최악의 경우 시간 복잡도가 O(N)이다.
→ 그러나, RB Tree는 삽입, 삭제 동안 트리의 모양이 균형 잡히도록 각 노드들은 Red 혹은 Black의 색상을 가지고 모든 경우에서 O(logN)의 시간 복잡도를 보장받는다.
사용 용도
- 커널 (Kernel) 내부 자료구조
- C 언어 기반 라이브러리/알고리즘의 Key-Value 저장
- 데이터베이스 인덱스 엔진
- 각종 기하학 계산
- 함수형 프로그래밍에서의 연관 배열, 집합
- C++의 map의 자료구조, 자바의 TreeMap의 자료구조
지켜야할 조건
- 모든 노드는 Red 또는 Black이다.
- 루트 노드는 Black이다.
- 모든 리프 노드(NIL)들은 Black이다.
→ NIL은 Null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드이다. - Red 노드의 자식은 Black이다.
→ Red가 연속적으로 나올 수 없다. - 모든 리프 노드에서 Black Depth는 같다.
→ 루트 노드에서 리프 노드까지 가는 경로에서 만나는 Black 노드의 개수가 같다.
위의 사용 조건을 무조건 따라야한다.
그리고 삽입이나 삭제 등 해당 과정을 수행하기전 RB Tree는 모든 조건을 통과한 트리 형태임을 꼭 기억하자.
📝 삽입 규칙과 과정
먼저 삽입을 진행하기 전에 삽입을 할 때 지켜져야하는 규칙을 살펴보겠다.
삽입 규칙
- 새 노드 삽입시 Red로 초기화 삽입
→ 왜 그럴까?
Black을 삽입하면 무조건 규칙 위반한다. (Black Depth가 무조건 안맞음)
그러나 Red를 삽입하면 위반 될 수도 안될 수도 있다. - 위치는 리프노드에서 삽입(NIL)
삽입 과정
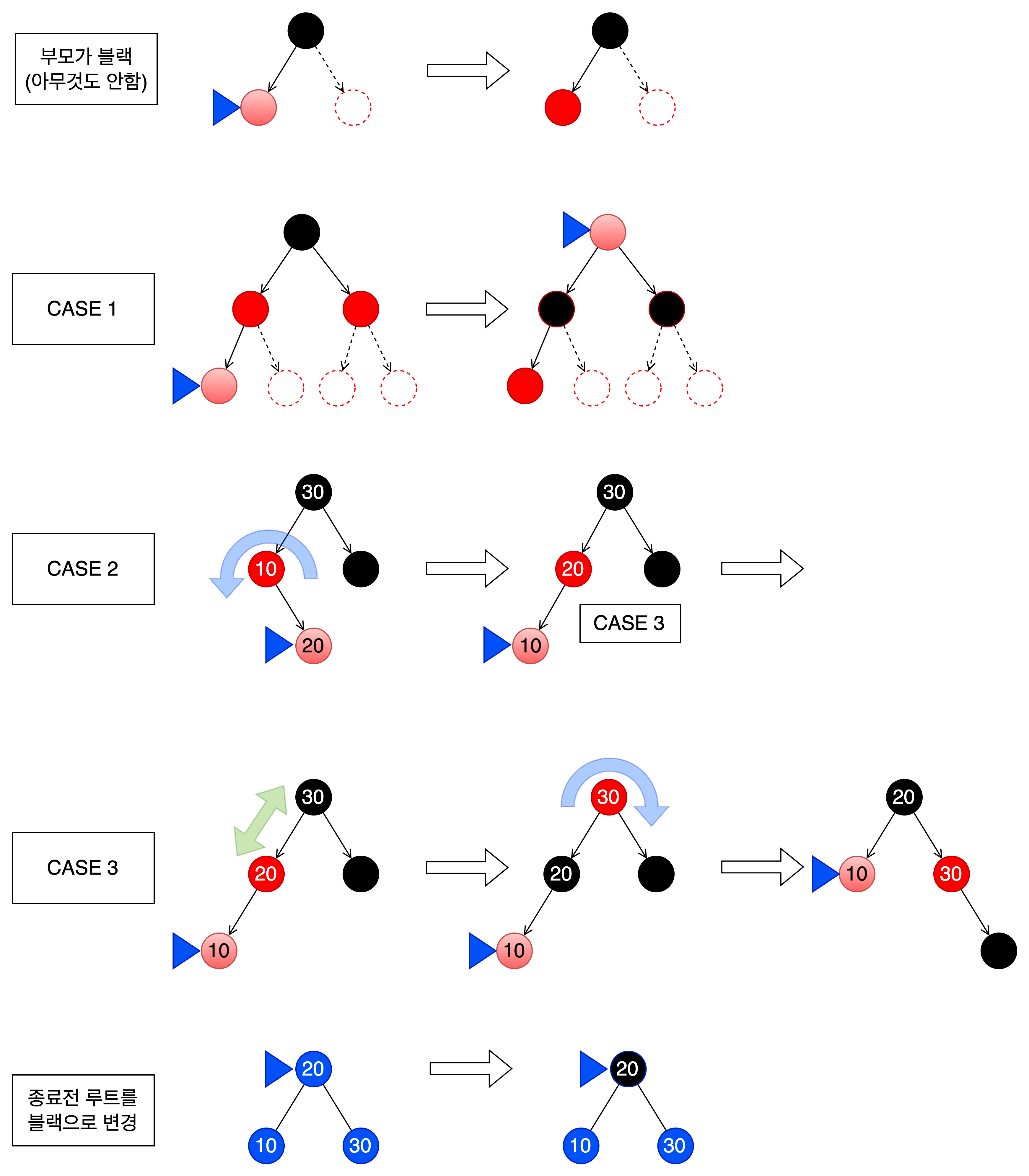
- 위의 삽입 규칙에 따라 Red로 새 노드를 삽입합니다.
- 삽입 후 리밸런싱 케이스, 부모가 Red인 경우만 문제가 발생한다.(4번 규칙)
2-1. 삼촌이 Red일 시, 부모와 삼촌을 색상 변경(Recoloring) 통해 해결(조부모가 루트가 아니면 재귀로 리밸런싱)
else
2-2. 삼촌이 Black이거나 존재하지 않을 시, 부모와 조부모의 색을 바꾸고 부모-자식의 방향성에 따라 LL, RR, LR, RL 케이스로 나누어 회전을 수행합니다.
3-1. LL 케이스, 부모와 조부모의 색을 바꾸고 Right Rotation을 수행하고 조건에 따라 색상 스왑을 합니다.
3-2. RR 케이스, 부모와 조부모의 색을 바꾸고 Left Rotation을 수행하고 조건에 따라 색상 스왑을 합니다.
3-3. LR 케이스, LL 케이스를 만들기 위해 Left Rotation을 수행하고 Right Rotation을 수행합니다.
3-4. RL 케이스, RR 케이스를 만들기 위해 Right Rotation을 수행하고 Left Rotation을 수행합니다. - Root 노드를 어떤 사항에서든 Black으로 바꿈.(Root의 부모가 없기 때문)
삽입 실습
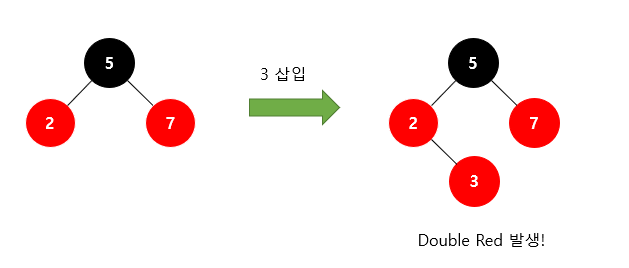
RB Tree에 3번을 Red로 초기화 하여 삽입한다.
이럴때, Double Red가 발생하고 삼촌의 색의 따라 두가지 방식을 사용할 수 있습니다.
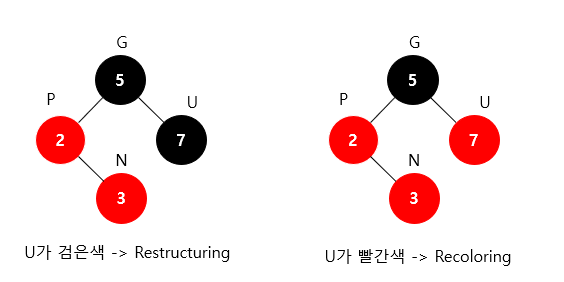
본인 노드인 새로 삽입한 노드는 N, 부모 노드를 P, 조부모를 G, 부모P의 형제를 삼촌(U)이라고 합니다.
만약에 Double Red를 발생했을 때,
삼촌 노드가 빨간색이라면, Recoloring을 수행합니다.
삼촌 노드가 검은색이라면, Restructing을 수행합니다.
- Recoloring(삼촌 노드가 빨간색일시)(Case1)
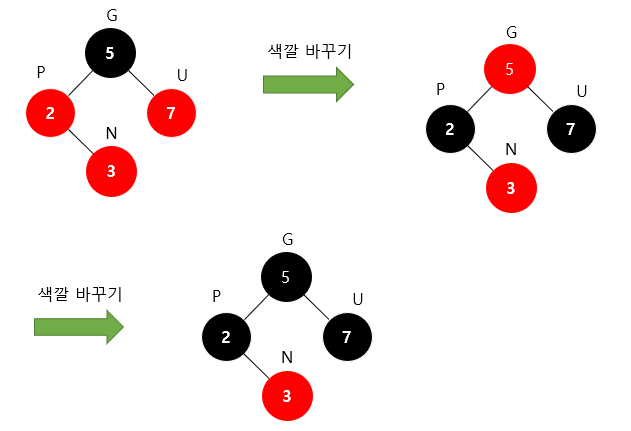
- 본인의 부모와 삼촌을 검은색으로 바꾸고 그에 따라 조부모도 빨간색으로 바꾼다.
1-1. 조부모가 루트 노드라면 검은색으로 바꾼다.
1-2. 조부모를 빨간색으로 바꿨을 때 또다시 Double Red가 발생한다면 또다시 Restructuring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.
삼촌이 빨간색이면 원래의 블랙 카운트가 1임을 유지하며 조건 4인 빨간색이 겹치지 않는다는 조건을 충족하기 위해 부모와 삼촌을 색을 바꾸고, 조부모의 색또한 바꾼다. 이후에 조부모는 무조건 검은색이어야하므로 검은색으로 바꿔야한다. 만약, 조부모 상단의 부모가 있다면 계속해서 색 변환을 진행해야한다.
여기서 기억해야되는건 4번 규칙이다. 검은색 노드는 2번 나와도 된다. 빨간색 노드가 2번 나오면 안 된다.

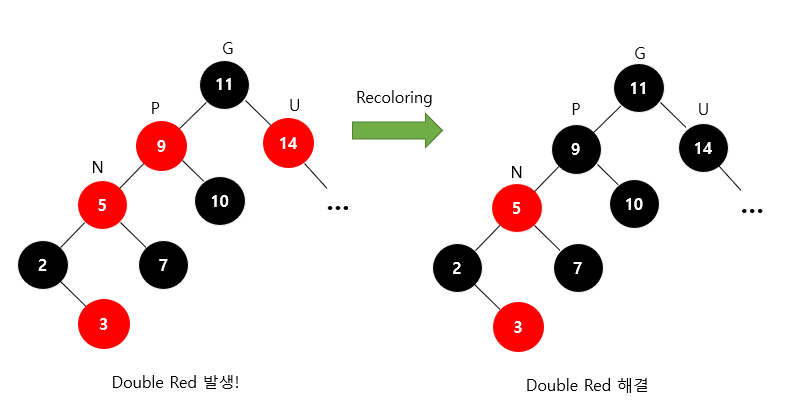
Recoloring은 간단해 보이지만 문제는 조부모 노드가 루트 노드가 아니면서, 조부모 노드가 또다시 Double Red 문제가 발생하는 경우이다. 이런 경우 1-2에 따라 Restructuring 혹은 Recoloring을 반복해서 실행한다.
- Restructing(삼촌 노드가 검은색일시)(Case2, 3)
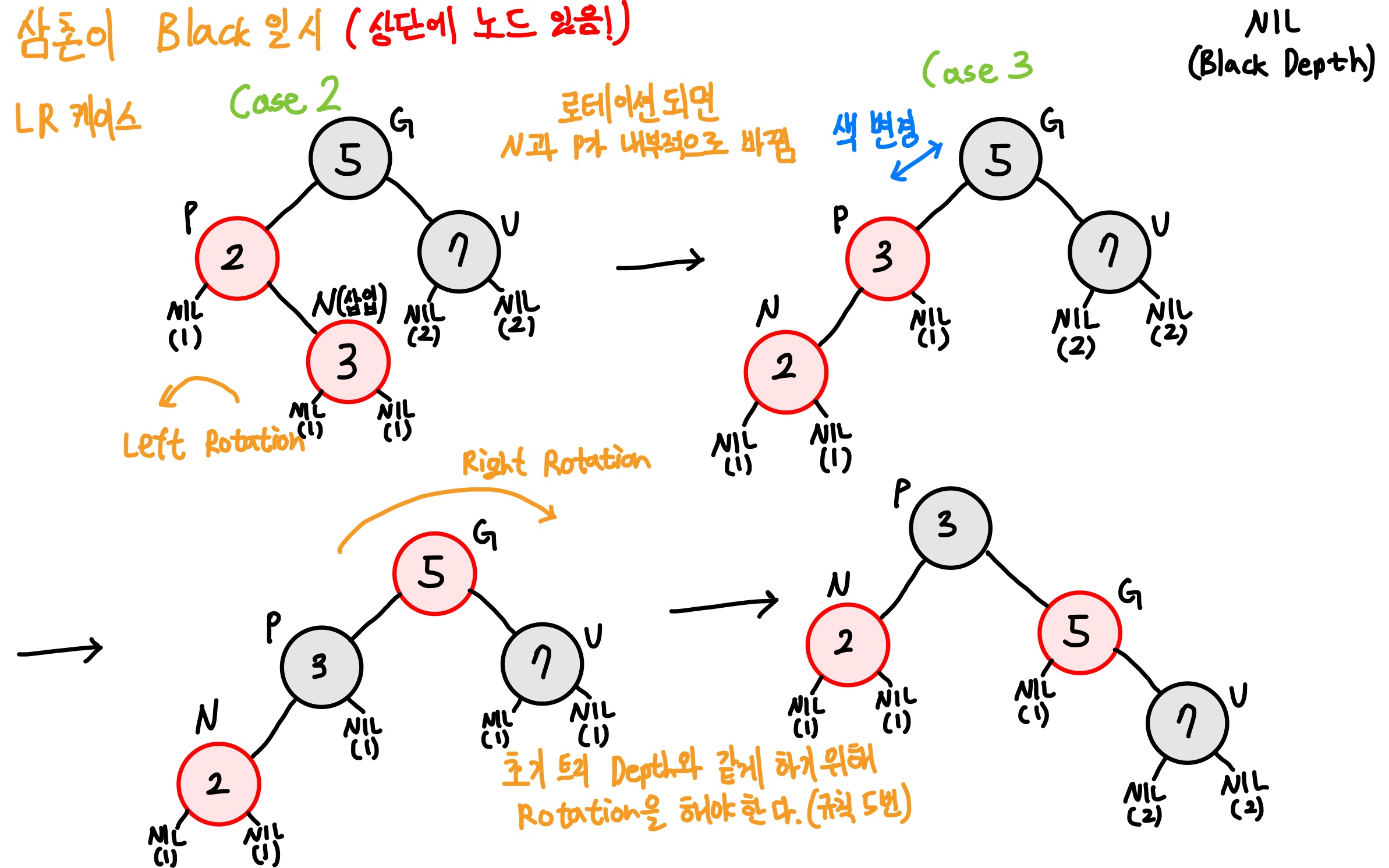
위에 서술한 것처럼 다양한 케이스들이 있지만, 대표적으로 LR 케이스일 때 과정을 설명해보겠다.
(Case 2)
1. LR 케이스의 경우, LL케이스로 만들어주기 위해 새로 삽입된 노드에 대해 Left Rotation을 먼저 수행합니다.
1-1. 균형을 맞추고, 4번 규칙 Red 노드가 연속으로 나오는 문제를 해결을 위해 부모와 조부모의 색을 바꿉니다.
(Case 3)
1-2. 이후 5번 규칙 NIL의 Black Depth를 맞춰주기 위해 부모기준 Right Rotation을 수행합니다.
해당 과정에서 주로 기억해야되는 점은 LL과 RR 케이스로 만들기 위해 Rotation을 적절히 수행합니다.(Case 2)
4번 규칙과 5번 규칙을 지키기 위해 부모, 조부모의 색을 서로 바꾸고 Rotation을 수행해야된다는 점입니다.(Case 3)
색 변경을 하고 회전을 하는 이유는 4번의 빨간색이 겹치지 않는다를 색을 변경하면서, 5번의 NIL의 횟수를 유지하여야 하므로 회전을 통해 해결한다.
→ 결론적으로 삽입은 5가지의 RB-Tree의 규칙을 꼭 준수하며(부모가 Red일시 고려) 삼촌의 색상에 따라 Recoloring(Red)과 Restructing(Black)을 수행하면 됩니다.
삽입 코드 구현(C언어)
[C언어 코드 구현]
삽입 코드는 크게 4가지의 함수가 필요합니다.
- 일반적인 상황에서 새 노드를 삽입하는 함수(새노드를 빨간색으로 삽입하고 NIL 위치에 오는등)
- RB Tree 5가지 조건에 따라 수정 작업을 해주는 함수
- 2번 코드의 수정 작업에서 필요한 left rotation 함수
- 3번과 방향만 다른 right rotation 함수
가 있습니다.
새 트리 생성 함수
// 새 트리 생성 함수
rbtree *new_rbtree(void) {
// tree 구조체 동적 할당
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
// NIL 노드 생성 및 초기화
node_t *nil = (node_t *)calloc(1, sizeof(node_t));
if (nil == NULL)
{
free(p);
return NULL;
}
nil -> color = RBTREE_BLACK; // NIL 노드는 항상 Black
nil->key = 0;
nil->parent = NULL;
nil->left = NULL;
nil->right = NULL;
// NIL 노드 생성 및 초기화
// tree의 nil과 root를 nil 노드로 설정 (tree가 빈 경우 root는 nil노드여야 한다.)
p -> nil = nil;
p -> root = nil;
return p;
}왼쪽 회전
// 왼쪽 회전
void left_rotation(rbtree *t, node_t *x) {
// x가 위에 있는 부모이고, y는 x의 오른쪽 아래의 자식이다.
node_t *y = x -> right; // x의 오른쪽 자식은 노드 y 이다.
x -> right = y -> left; // y의 왼쪽 자식을 x의 오른쪽 자식으로 회전한다.
if ( y -> left != t -> nil) { // y의 왼쪽 자식이 비어 있지 않은 경우
y -> left -> parent = x; // y의 왼쪽 자식의 부모는 x가 된다.
}
y -> parent = x -> parent; // x의 부모는 y의 부모가 된다.
// 여기까지 y를 x자리로 올리기 위해 y의 자식을 x의 자식으로 처리하고 y를 x의 부모로 대체하는 과정이다. (y에 자식이 있을때)
if (x -> parent == t -> nil) { // x의 부모가 t는 nil(없을때)일때, 즉 x가 루트일때
t -> root = y; // y가 트리의 루트가 된다.
}
else if (x == x -> parent -> left) { // x가 부모의 왼쪽 자식일때
x -> parent -> left = y; // x의 부모의 왼쪽 자식을 y로 대체
}
else { // 그외의 경우(x는 부모의 오른쪽 자식이었다
x -> parent -> right = y; // x의 부모의 오른쪽 자식을 y로 대체
}
y -> left = x; // x를 y의 왼쪽 자식으로 둔다
x -> parent = y; // y룰 x의 부모로 둔다
// 여기까지 x가 루트였으면 y를 루트로 두고, x가 부모가 있었으면 그 부모를 y의 부모로 바꾸는 과정이다.
// 이후 마지막 두 문장은 x와 y의 부모, 자식 관계를 재정립한다.
}오른쪽 회전
// 오른쪽 회전
void right_rotation(rbtree *t, node_t *x) {
// x가 위에 있는 부모이고, y는 x의 왼쪽 아래의 자식이다.
node_t *y = x -> left; // x의 왼쪽 자식은 노드 y 이다.
x -> left = y -> right; // y의 오른쪽 자식을 x의 왼쪽 자식으로 회전한다.
if ( y -> right != t -> nil) { // y의 오른쪽 자식이 비어 있지 않은 경우
y -> right -> parent = x; // y의 오른쪽 자식의 부모는 x가 된다.
}
y -> parent = x -> parent; // x의 부모는 y의 부모가 된다.
// 여기까지 y를 x자리로 올리기 위해 y의 자식을 x의 자식으로 처리하고 y를 x의 부모로 대체하는 과정이다. (y에 자식이 있을때)
if (x -> parent == t -> nil) { // x의 부모가 t는 nil(없을때)일때, 즉 x가 루트일때
t -> root = y; // y가 트리의 루트가 된다.
}
else if (x == x -> parent -> right) { // x가 부모의 오른쪽 자식일때
x -> parent -> right = y; // x의 부모의 오른쪽 자식을 y로 대체
}
else { // 그외의 경우(x는 부모의 오른쪽 자식이었다
x -> parent -> left = y; // x의 부모의 왼쪽 자식을 y로 대체
}
y -> right = x; // x를 y의 오른쪽 자식으로 둔다
x -> parent = y; // y룰 x의 부모로 둔다
// 여기까지 x가 루트였으면 y를 루트로 두고, x가 부모가 있었으면 그 부모를 y의 부모로 바꾸는 과정이다.
// 이후 마지막 두 문장은 x와 y의 부모, 자식 관계를 재정립한다.
}insert fix 함수
(삽입과정에서 RB트리 규칙에 따라 수정)
// 삽입에서 넘긴 값을 토대로 수정 수행
void insert_fix(rbtree *t, node_t *new_node) {
node_t *uncle; // 삼촌을 정의
while (new_node -> parent -> color == RBTREE_RED) { // 삽입한 부모 노드의 색깔이 Red 일때까지 실행
// 부모가 왼쪽일때 과정
if (new_node->parent == new_node->parent->parent->left) { // 새 노드의 부모가 조부모의 왼쪽일때
uncle = new_node->parent->parent->right; // 삼촌은 새 노드의 조부모의 오른쪽 자식임
// Case 1
if (uncle -> color == RBTREE_RED) { // 삼촌의 색이 빨간색인 케이스
new_node -> parent -> color = RBTREE_BLACK; // 새 노드의 부모는 검은색으로 지정
uncle -> color = RBTREE_BLACK; // 삼촌 또한 검은색으로 지정
new_node -> parent -> parent -> color = RBTREE_RED; // 조부모는 빨간색으로 지정
new_node = new_node -> parent -> parent; // 조부모까진 완벽하니, 조부모를 새 노드로 지정하고 재확인
}
else {
if (new_node == new_node -> parent -> right) { // 새 노드가 부모의 오른쪽에 있을때
// Case 2
new_node = new_node -> parent; // 새 노드를 부모로 지정
left_rotation(t, new_node); // 새 노드의 부모를 기준으로 왼쪽 로테이션 돌림
}
// Case 3(위치는 바꿨으니 색을 바꿔줘야함)
new_node -> parent -> color = RBTREE_BLACK; // 새 노드의 부모를 검은색으로 지정
new_node -> parent -> parent -> color = RBTREE_RED; // 조부모는 빨간색으로 지정
right_rotation(t, new_node -> parent -> parent); // 조부모 기준으로 오른쪽 로테이션 돌림
}
}
// 위의 케이스와 다르게 부모가 오른쪽일때 과정
else {
uncle = new_node->parent->parent->left; // 삼촌은 새 노드의 조부모의 왼쪽 자식임
// Case 1
if (uncle -> color == RBTREE_RED) { // 삼촌의 색이 빨간색인 케이스
new_node -> parent -> color = RBTREE_BLACK; // 새 노드의 부모는 검은색으로 지정
uncle -> color = RBTREE_BLACK; // 삼촌 또한 검은색으로 지정
new_node -> parent -> parent -> color = RBTREE_RED; // 조부모는 빨간색으로 지정
new_node = new_node -> parent -> parent; // 조부모까진 완벽하니, 조부모를 새 노드로 지정하고 재확인
}
else {
if (new_node == new_node -> parent -> left) { // 새 노드가 부모의 오른쪽에 있을때
// Case 2
new_node = new_node -> parent; // 새 노드를 부모로 지정
right_rotation(t, new_node); // 새 노드의 부모를 기준으로 오른쪽 로테이션 돌림
}
// Case 3(위치는 바꿨으니 색을 바꿔줘야함)
new_node -> parent -> color = RBTREE_BLACK; // 새 노드의 부모를 검은색으로 지정
new_node -> parent -> parent -> color = RBTREE_RED; // 조부모는 빨간색으로 지정
left_rotation(t, new_node -> parent -> parent); // 조부모 기준으로 왼쪽 로테이션 돌림
}
}
}
t -> root -> color = RBTREE_BLACK; // 루트는 항상 검은색이어야하는 규칙(루트의 부모는 없기 때문에 색을 검은색으로 지정해도됨)
}insert 함수
본격적인 삽입 함수
// 삽입
node_t *rbtree_insert(rbtree *t, const key_t key) {
// 책에서는 새 노드가 z라고 나오는데,
// 해당 코드에선 z가 new_node로, new_node에 이미 키가 삽입되어 있다.
// 노드생성
node_t *new_node = (node_t *)calloc(1, sizeof(node_t));
if (new_node == NULL) {
return NULL; // 또는 에러 메시지 출력 후 return
}
// 새로 추가할 노드 값 초기화
new_node -> key = key; // 새 노드안에 들어가는 값은 key
// new_node -> color = RBTREE_RED; // 무조건 새 노드 들어갈때 빨강 지정
// new_node -> left = t -> nil; // 새 노드의 왼쪽 자식 노드는 nil
// new_node -> right = t -> nil; // 새 노드의 오른쪽 자식 노드는 nil
node_t *x = t -> root; // x는 루트 노드에서 시작 (트리를 따라 내려감)
// 현재 탐색 중인 노드 x(비교 대상)
node_t *y = t -> nil; // y는 x의 부모를 기억할 변수 (초기에는 nil)
// y는 삽입될 위치의 부모 노드
// 삽입 시작
while (x != t -> nil) { // x가 nil일 때 까지 내려간다(경계 NIL에 도달할 때까지 내려간다)
y = x; // 초기에는 y는 x이다.
// 밑으로 내려가면서 새 노드를 삽입할 적당한 위치를 찾는다.
if (new_node -> key < x -> key) { // 새노드의 키(값)가 x노드의 키(값)보다 작을때
x = x -> left; // x노드는 x의 오른쪽에 온다
}
else { // 반대의 경우
x = x -> right; // x노드는 x의 오른쪽에 온다
}
}
new_node -> parent = y; // y는 새 노드의 부모님으로 지정
// 여기까지 탐색대상 x를 내리며 값이 작으면 왼쪽 자식을 탐색하고 크면 오른쪽 자식을 탐색한다.
if (y == t -> nil) { // y가 nil이면(트리에 아무것도 없었다)
t -> root = new_node; // 새 노드는 루트이다
}
else if (new_node -> key < y -> key) { // 새 노드의 키가 y(부모)의 키보다 작으면
y -> left = new_node; // 새 노드는 y의 왼쪽 자식에 온다
}
else { // 그외의 케이스, 새 노드가 y보다 크면
y -> right = new_node; // 새 노드는 y의 오른쪽 자식에 온다
}
// 새노드를 삽입하기 위해 부모 y를 기준으로 키값을 비교하여 자식값에 넣는다.
// 새노드에 왼쪽, 오른쪽 자식에 NIL을 추가, 새 노드는 빨강으로 지정
new_node -> left = t -> nil;
new_node -> right = t -> nil;
new_node -> color = RBTREE_RED;
// 수정 작업 수행(트리와 새 노드값을 넘김)
insert_fix(t, new_node);
return new_node;
}🗑️ 삭제 규칙과 케이스
삭제를 할 때 지켜져야하는 규칙을 살펴보겠다. 삽입보다 어려우니 RBtree 조건과 4가지 케이스를 유념하며 코드를 짜야한다.
삽입 규칙
-
노드 삭제 전 BST 방식으로 진행
삭제할 노드가 두 개의 자식을 가지고 있다면, 일반 BST처럼 후계자(successor) 또는 전임자(predecessor)로 교체 후 삭제합니다.
→ 실제 삭제는 리프 노드 또는 하나의 자식만 있는 노드에서 발생하게 됩니다.
-
삭제되는 노드가 빨강인 경우
- 삭제해도 속성이 깨지지 않기 때문에 단순 삭제만 하면 됩니다.
-
삭제되는 노드가 검정인 경우
- ‘이중 검정(double black)’ 상태가 발생할 수 있고, 이를 해결하기 위해 다양한 회전 및 색상 변경 작업이 필요합니다.
삭제 케이스
- Case 1: 형제가 빨강
부모와 형제의 색을 바꾸고, 부모를 회전하여 검정 형제로 바꾼 후 다음 케이스로 진행합니다. - Case 2: 형제와 형제의 자식들이 모두 검정
형제를 빨강으로 변경하고, 부모를 기준으로 위로 올라가며 반복합니다. - Case 3: 형제가 검정이고, 가까운 자식이 빨강
형제와 자식의 색을 바꾸고 형제를 회전하여 Case 4로 전환합니다. - Case 4: 형제가 검정이고, 먼 자식이 빨강
형제의 색을 부모의 색으로 바꾸고, 부모와 먼 자식의 색을 검정으로 바꾼 후 부모를 기준으로 회전합니다. 이후 종료합니다.
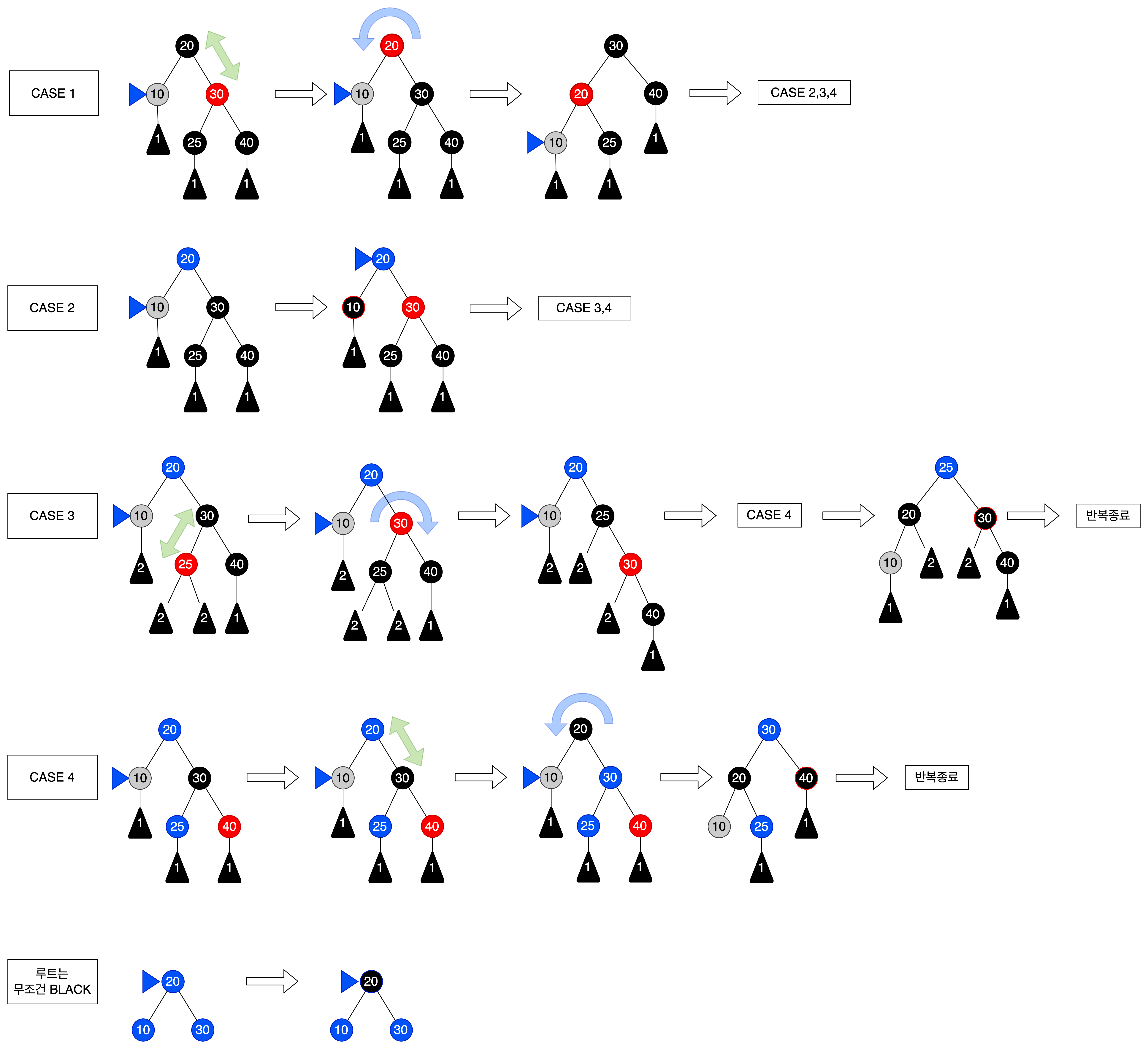
Case 1
w가 Red일 시, 자식들은 Black입니다. 이들은 NIL일수 없습니다. 만약, NIL이면 5번 조건이 충족되지 않기 때문입니다. x 더블 블랙을 없애는 것이 핵심이다.
→ w를 Black으로 변경해 준후, B를 Red로 변경합니다. D를 기준으로 left-roatation을 적용합니다. 기존의 w의 자식이었던 C는 B의 자식으로 편입됩니다.
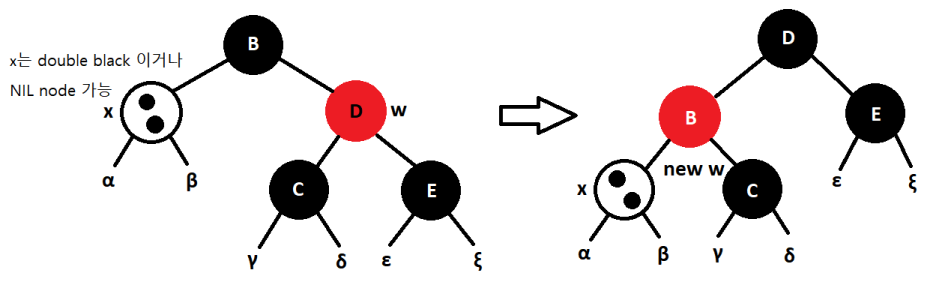
Case 2
w가 Black일시, w의 자식들도 Black인 경우 입니다. 회색 노드는 Black / Red 둘다 가능합니다.
여기서 생각해야하는 것은 자식의 두개의 Black을 받아 부모가 Black이 될 수 있습니다.
→ x의 Black을 B에게 전달하고, w를 Red로 바꿉니다. B를 새로운 x로 지정합니다.
만약, Case1에서 이 경우에 도착했다면 x는 Red였고, 새로운 x는 Red와 Black이 되었습니다. 그러면 Black으로 변경하고 끝내면 됩니다. 사실상 B가 자식 두개의 Black을 받아서 Black이 됐습니다.
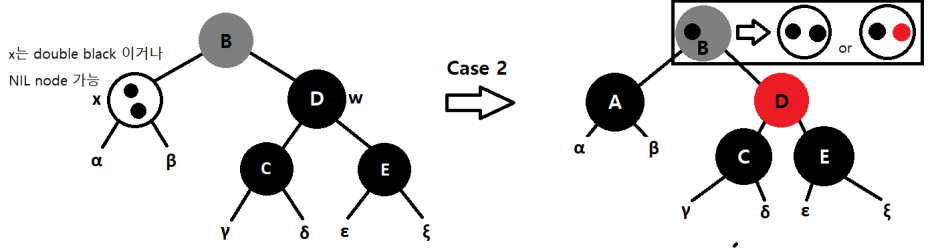
Case 3
w는 Black이고 w의 왼쪽자식이 Red일때, 안쪽에 있는 Red 자식을 회전을 통해 밖으로 빼줘야합니다.
→ w를 Red로 변경하고 w의 왼쪽 자식을 Black으로 변경합니다. 이후 w에 대해 right rotation을 적용합니다. x의 새로운 형제 w는 오른쪽 자식이 Red입니다. 이후는 Case 4를 통해 해결합니다.
Case 4

w는 Black이고 w의 오른자식이 Red일때, w와 B의 색을 교환합니다.(w의 색을 현재 B의 색인 Black으로 변경합니다.) w의 오른쪽 자식 E를 Black으로 변경합니다.
D에 대해 left rotation을 적용 후, x의 extra Black을 제거한 후 종료합니다.(Black Depth 유지)
+[직관적인 설명]
D의 Black 을 C와 E에 나누어줍니다. 그러면 D는 Red가 됩니다. C는 더블 블랙이되고, E는 블랙이 됩니다. 해당 상태에서 B와 D색을 서로 바꿔 left rotation을 해주면 B는 빨간색이되고 D가 원래의 B의 색(Red or Black)이 됩니다. 그러면 B의 왼쪽 자손인 본래의 더블 블랙과 C에서 온 더블 블랙이 만나 B가 Red에서 Black으로 바뀝니다. 그러면 Case4를 완료할 수 있습니다.
이에 따라 B가 어떤 색이든 상관없습니다.
→ 최종적으로 삭제는 두가지 케이스로 바꿔서 해결해야한다.
- 자식 노드 Red가 밖인 outer case로 만들고 해결
- 루트를 자식들 두개의 더블 블랙(블랙)을 통해 Black으로 만들고 해결
삭제 코드 구현(C언어)
C언어 코드 구현
삽입 코드는 크게 4가지의 함수가 필요합니다.
- 삭제에서 노드가 하나의 자식만 가질 때, 두 자식을 가질 때 후임자와 교체하기 위한 Transplant함수
- 특정노드의 후손을 찾는 함수인 minimum 함수
- RB tree의 조건에 따라 삭제 과정을 수정하는 erase fix 함수
- 삭제의 전체적인 흐름을 제어하는 erase 함수
후임자 교체 함수
// 삭제에서 노드가 하나의 자식만 가질 때, 두 자식을 가질때 후임자와 교체(부모와 후임자와 교체)
// u노드를 v로 대체함
void Transplant(rbtree *t, node_t * u, node_t *v) {
if (u -> parent == t -> nil) { // u의 부모가 NULL일때 (루트일때?)
t -> root = v; // v(후임자)가 트리의 루트이다
}
else if (u == u -> parent -> left) { // u가 u의 부모 왼쪽 자식과 같으면
u -> parent -> left = v; // u의 부모의 왼쪽 자식을 v로 대체
}
else { // u가 u의 부모 오른쪽 자식과 같으면
u -> parent -> right = v; // u의 부모의 오른쪽 자식을 v로 대체
}
v -> parent = u -> parent; // v의 부모는 u의 부모와 같다
}특정노드의 후손을 찾는 함수
// 특정노드 p의 후손을 찾음
node_t *minimum(rbtree *t, node_t *p) {
node_t *cur = p; // cur로 p의 후손을 찾는다.
while(cur -> left != t -> nil) { // cur 왼쪽 자식이 nil이 나올때까지 시행
cur = cur -> left; // cur을 왼쪽 자식으로 보낸다.
}
return cur; // cur을 리턴한다(erase로 보냄)
}erase fix 함수
(삭제 과정에서 RB트리 규칙에 따라 수정)
// 지우는 과정에서의 RB 트리 규칙에 따라 수정
void erase_fix(rbtree *t, node_t *x) {
node_t *w = x; // 형제 노드를 가리키기 위한 포인터 초기화 (임시)
// x가 루트가 아니고, 검은색 노드일 때까지 반복 (균형 깨진 상태)
while (x != t->root && x->color == RBTREE_BLACK) {
// case: x가 부모의 왼쪽 자식일 경우
if (x == x->parent->left) {
w = x->parent->right; // 형제 노드 w는 부모의 오른쪽 자식
// case 1: 형제 w가 빨강일 때
if (w->color == RBTREE_RED) {
w->color = RBTREE_BLACK; // 형제를 검정으로
x->parent->color = RBTREE_RED; // 부모는 빨강으로
left_rotation(t, x->parent); // 부모를 기준으로 좌회전
w = x->parent->right; // 회전 후 w를 다시 지정
}
// case 2: 형제의 양쪽 자식이 모두 검정
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK) {
w->color = RBTREE_RED; // 형제를 빨강으로 칠함
x = x->parent; // x를 부모로 올려서 fix 계속 진행
}
// case 3 or 4
else {
// case 3: 형제의 오른쪽 자식이 검정
if (w->right->color == RBTREE_BLACK) {
w->left->color = RBTREE_BLACK; // 형제의 왼쪽 자식을 검정으로
w->color = RBTREE_RED; // 형제를 빨강으로
right_rotation(t, w); // 형제를 기준으로 우회전
w = x->parent->right; // w 업데이트
}
// case 4: 형제의 오른쪽 자식이 빨강 (case 3을 거쳐 오기도 함)
w->color = x->parent->color; // 형제는 부모의 색을 물려받고
x->parent->color = RBTREE_BLACK; // 부모는 검정
w->right->color = RBTREE_BLACK; // 형제의 오른쪽 자식도 검정
left_rotation(t, x->parent); // 부모 기준으로 좌회전
x = t->root; // x를 루트로 설정하고 루프 종료
}
}
// case: x가 부모의 오른쪽 자식일 경우 (위와 좌우 반대)
else {
w = x->parent->left; // 형제 노드는 왼쪽 자식
// case 1: 형제가 빨강일 때
if (w->color == RBTREE_RED) {
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotation(t, x->parent);
w = x->parent->left;
}
// case 2: 형제 자식 둘 다 검정
if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK) {
w->color = RBTREE_RED;
x = x->parent;
}
// case 3 or 4
else {
// case 3: 형제의 왼쪽 자식이 검정
if (w->left->color == RBTREE_BLACK) {
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotation(t, w);
w = x->parent->left;
}
// case 4
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotation(t, x->parent);
x = t->root;
}
}
}
// 루프가 끝나면 x의 색을 검정으로 (속성 회복)
x->color = RBTREE_BLACK;
}erase 함수
(본격적인 삭제함수)
// y: 실제로 삭제되거나 트리 구조에서 제거될 노드
// x: erase_fix()에서 사용할 삭제된 자리를 채우는 노드
// y_origin_color: 삭제 전 노드의 색을 기억 → 검정이면 erase_fix()가 필요함
int rbtree_erase(rbtree *t, node_t *p) {
node_t *y = p; // 추후에 p를 따로 쓰기 위해 y로 노드 인자 추가
node_t *x = p; // 추후에 p를 따로 쓰기 위해 x로 노드 인자 추가
color_t y_origin_color = y -> color; // y 컬러를 나중에 쓰기 위해 y_origin_color로 저장
if (p -> left == t -> nil) { // 기준p의 왼쪽 자식이 NIL이면 수행
x = p -> right; // x를 p의 오른쪽 자식이라고 지정
Transplant(t, p, p -> right); // p를 오른쪽 자식으로 바꾼다.
}
else if (p -> right == t -> nil) { // p의 오른쪽 자식인 NIL이라면
x = p -> left; // x를 p의 왼쪽자식으로 지정
Transplant(t, p, p -> left); // p를 왼쪽 자식으로 바꾼다.
}
else {
y = minimum(t,p -> right); // p를 오른쪽 자식으로 바꾼다.
y_origin_color = y -> color; // y의 원래 컬러를 저장한다
x = y -> right; // x는 y의 오른쪽 자식이다.
////////// 해당 부분 문제 //////
// if (y->parent == p)
// x->parent = y;
// else {
// Transplant(t, y, y->right);
// y->right = p->right;
// y->right->parent = y;
// }
// Transplant(t, p, y);
// y->left = p->left;
// y->left->parent = y;
// y->color = p->color;
// }
////////// 수정전 ////////
if (y != p -> right) { // y가 트리에서 더 아래쪽인가?
Transplant(t, y, y -> right); // y를 오른쪽 자식으로 바꾼다.
y -> right = p -> right;
y -> right -> parent = y;
}
else { // 해당 else문을 잘못 들여쓰기 했다.
x -> parent = y; // x가 NIL인 경우
}
Transplant(t, p, y); // p를 그 후손인 y로 바꾼다.
y -> left = p -> left; // z의 왼쪽 자식을 y에 부여한다.
y -> left -> parent = y; // 왼쪽 자식이 없는 y
y -> color = p -> color;
}
//////////////////////////////
if (y_origin_color == RBTREE_BLACK) { // 레드 블랙 위반이 발생한 경우
erase_fix(t, x); // 수정한다.
}
return 0;
}⚒️ delete_rbtree, find, min, max, array 함수 구현
정글에서 주어진 RB Tree에는 삽입, 삭제 뿐만 아니라 delete_rbtree(트리 전체 삭제), find, max, min, array 함수들을 추가로 구현해야했습니다.
- delete_rbtree 함수는 작업이 끝난 트리의 메모리를 free를 통해 해제하면 됩니다.
- find 함수는 주어진 key값을 비교를 통해 트리에서 찾으면 됩니다.
- min 함수는 트리에서 값이 가장 작은 key 값을 반환하면 됩니다.
- max 함수는 트리에서 값이 가장 큰 key 값을 반환하면 됩니다.
- array 함수는 주어진 n크기만큼의 배열에 트리의 key 값 순서대로 저장하여 출력하면 됩니다.
구현 방식과 힌트들은 아래 코드의 주석을 참고하시면 좋을 것 같습니다.
delete_rbtree 함수 구현
// RB 트리는 자식과 부모가 연계되어 있으므로 노드 자체의 메모리해제를 따로 해야한다.
// 왼쪽 자식 -> 오른쪽 자식 -> 자기자신 순으로 해제한다.
void free_node(rbtree *t, node_t *del) {
if(del == t -> nil) { // 받은 노드가 NULL이면 그냥 리턴
return;
}
free_node(t, del -> left); // 왼쪽 자식 메모리 해제하기 위해 재귀
free_node(t, del -> right); // 오른쪽 자식 메모리 해제하기 위해 재귀
free(del); // 메모리 해제
}
// 모든 노드들 해제 후! NIL, RB 트리 구조체 해제
void delete_rbtree(rbtree *t) {
free_node(t, t -> root); // 루트를 시작점으로 모든 자식 노드를 순회하며 해제
free(t -> nil); // 공통의 NIL들 해제
free(t); // 트리 구조체 해제
}find 함수 구현
// 노드 검색
node_t *rbtree_find(const rbtree *t, const key_t key) {
node_t *cur = t -> root; // cur은 루트부터 시작
while(cur != t -> nil) { // cur 현재 확인 중인 노드가 NIL 될때까지 실행
if(cur -> key == key) { // 현재 비교하는 cur과 키값이 같을때
return cur; // cur 반환
}
if(cur -> key < key) { // 지금 확인중인 cur보다 키값이 클때
cur = cur -> right; // 오른쪽 자식으로 검색
}
else {
cur = cur -> left; // cur보다 키값이 작을때, 왼쪽 자식으로 검색
}
}
if(cur == t -> nil) { // cur이 없을때(트리가 없을때)
return NULL; // NULL 반환
}
return cur; // 값 리턴
}
min 함수 구현
// 최솟값 탐색
node_t *rbtree_min(const rbtree *t) {
node_t *cur = t -> root; // cur은 루트부터 시작
if(cur == t -> nil){ // 먼저 트리에 아무것도 없을 예외상황을 처리해야한다
return NULL; // 밑에 while문에 포함시키면 RB트리에서 맨밑이 항상 NIL이라 항상 NULL 나옴
}
node_t *min = NULL;
while(cur != t -> nil) { // NIL 만나기 직전까지 진행
min = cur; // NIL 만나기전 현재 노드를 기억
cur = cur -> left; // 최솟값으로 left로만 가야함
}
return min; // 값 리턴
}max 함수 구현
// 최댓값 탐색
node_t *rbtree_max(const rbtree *t) {
node_t *cur = t -> root; // cur은 루트부터 시작
if(cur == t -> nil){ // 먼저 트리에 아무것도 없을 예외상황을 처리해야한다
return NULL; // 밑에 while문에 포함시키면 RB트리에서 맨밑이 항상 NIL이라 항상 NULL 나옴
}
// 최댓값 검색
node_t *max = NULL;
while(cur != t -> nil) { // NIL 만나기 직전까지 진행
max = cur; // NIL 만나기전 현재 노드를 기억
cur = cur -> right; // 최댓값으로 right로만 가야함
}
return max; // 값 리턴
}
int rbtree_erase(rbtree *t, node_t *p) {
// TODO: implement erase
return 0;
}array 함수 구현
// 키값이 주어진 n 크기까지의 배열의 개수를 출력(중위순회)
// 내부에서 쓰는 재귀함수로 실제 트리를 순회하며 데이터를 배열에 넣음
void to_array(const rbtree* t, key_t *arr, const size_t n, node_t* cur, int* count) {
if(*count >= n || cur == t -> nil) return;
// count는 지금까지 배열에 저장한 key의 개수, n은 배열에 담을 수 있는 최대 개수
// 그러므로count가 주어진 n보다 커지거나 같아지면 바로 리턴
// 맨마지막인 NIL까지 내려가서 순회 종료
// 중위순회
to_array(t, arr, n, cur -> left, count); // 왼쪽 자식 맨끝부터 시작
if(*count < n) { // n횟수만큼 카운트가 진행
arr[*count] = cur -> key; // 배열에 현재 진행중인 키를 저장
*count += 1; // 배열에 저장한 횟수 +1
}
to_array(t, arr, n, cur -> right, count); // 오른쪽을 순회하고 끝냄
}
// 사용자가 호출하는 함수 역할로 외부에선 해당 함수만 호출(트리, 배열, 사이즈 n만 호출해 사용)
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
int count = 0; // count 0으로 초기화
to_array(t, arr, n, t -> root, &count);
// &count인 이유는 하단의 *count가 포인터로 인자를 줄려면 & 주소로 보내줘야한다.(값 변경을 반영)
return 0; // 값 리턴
}