알고리즘 01 재귀함수 기본 | 팩토리얼, 거듭제곱, 피보나치, GCD(최대공약수), 이진탐색) 외 | JS

1. What is Recursion?

재귀란 무엇인가

• 하나의 함수에서 자신을 다시 호출하여 작업을 수행하는 방식
  
  이미지 출처

재귀함수: 무한루프

function recursion() {
  console.log("here");
  recursion();
}

recursion() // 무한 루프

재귀함수: 무한루프 개선

function recursion(count) {
  if (count < 0) return // 반복을 멈출 조건을 설정

  console.log("here", count);
  recursion(count - 1); // 인수 업데이트 및 재귀 함수 호출
}

let count = 4;
recursion(count) 

• 개념적으로 다시보기

function recursion(count) {
  if (count < 0) return // base case
  // 적어도 하나의 recursion에 빠지지 않는 경우가 존재해야 함

  console.log("here", count);
  recursion(count - 1); // Recursive case
  // recursion을 반복하다보면 결국 base case로 수렴해야 함.

}

let count = 4;
recursion(count) 

• 적어도 하나의 recursion에 빠지지 않는 경우가 존재해야 함
• recursion을 반복하다보면 결국 base case로 수렴해야 함

1~n 까지의 합 구하기

// 이 함수의 mission은 0~n까지의 합을 구하는 것
function recursion(num) {
  if (num === 0) { 
    // n=0이라면 합은 0
    return 0 
  } else {
    // n이 0보다 크다면 0에서 n까지의 합은 0에서 n-1까지의 합에 n을 더한 값
    return num + recursion(num - 1);
  }
}

let num = 4;
recursion(num)

팩토리얼(Factorial: n!)

• 0! = 1
• n! = n*(n-1)! (n>0)
  

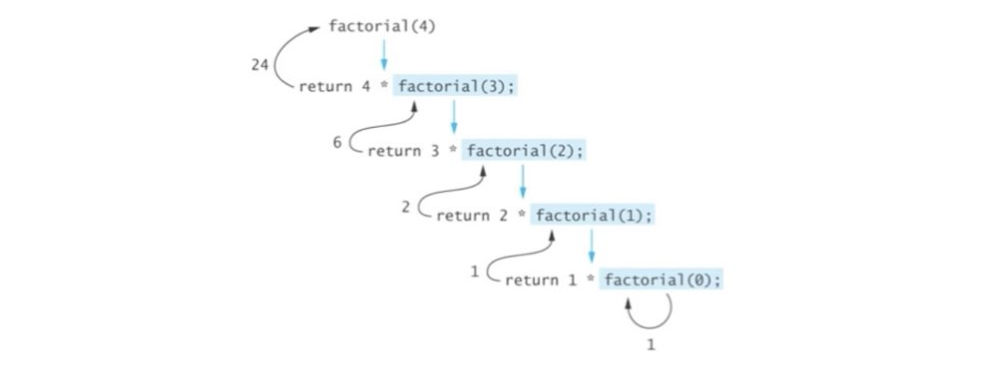
function factorial(n) {
  if (n === 0) {
    return 1
  } else {
    return n * factorial(n - 1)
  }
}

let n = 4;
factorial(n)

거듭제곱

• num^0 = 1
• num^n = n * n^n-1 (n > 0)

function power(num, n) {
  if (n === 0) {
    return 1
  } else {
    return num * power(num, n - 1)
  }
}

const num = 2
const n = 4;
power(num, n)

피보나치

• f(0) = 0
• f(1) = 1
• f(n) = f(n-1) + f(n-2) (n>1)

function fibonacci(n) {
  if (n < 2) {
    return n
  } else {
    return fibonacci(n - 1) + fibonacci(n - 2)
  }
}

const n = 4;
fibonacci(n)

최대공약수 | GCD

• Greatest Common Divisor: Euclid Method
• 앞의 수가 더 커야만 성립하기 때문에 검사 후 자리를 바꿔주는 로직 필요

function gcd(a, b) {
  if (a < b) {
    let temp = a
    a = b
    b = temp
  }
  if (a % b === 0) {
    return b
  } else {
    return gcd(b, a % b)
  }
}

const a = 12;
const b = 8;
gcd(a, b)

최대공약수 개선

• 두 수의 대소 관계가 무관하도록 개선

function gcd(a, b) {
  if (b === 0) {
    return a
  } else {
    return gcd(b, a % b)
  }
}

const a = 8;
const b = 12;
gcd(a, b)

2. Recursive Thinking

순환적으로 사고하기

문자열의 길이 계산

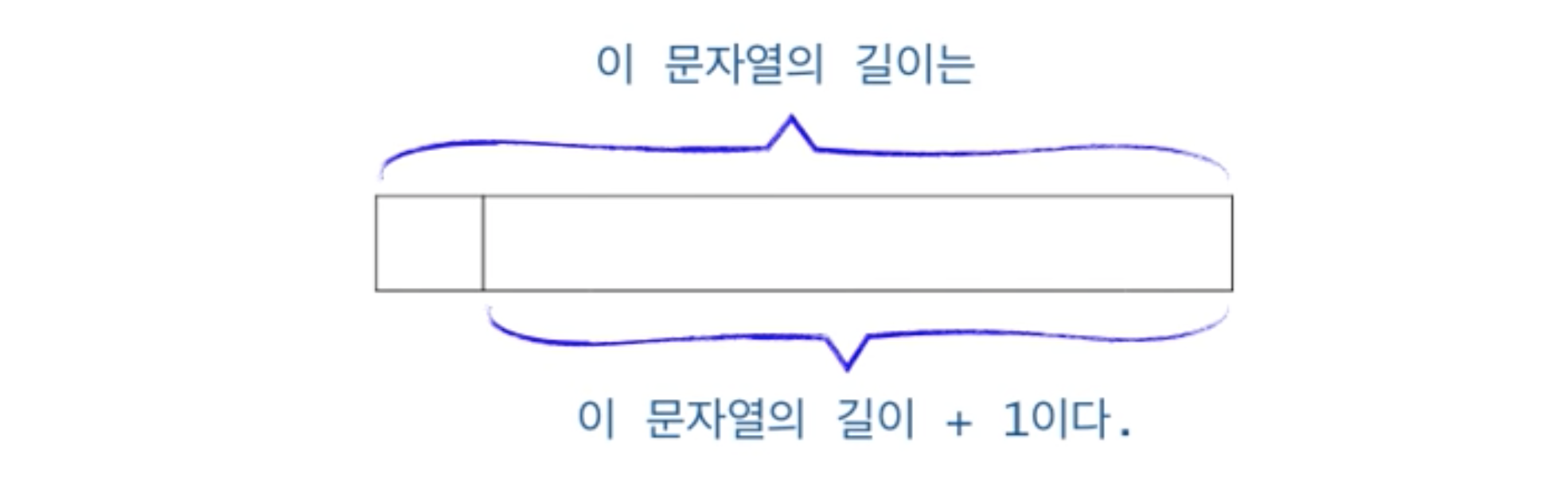
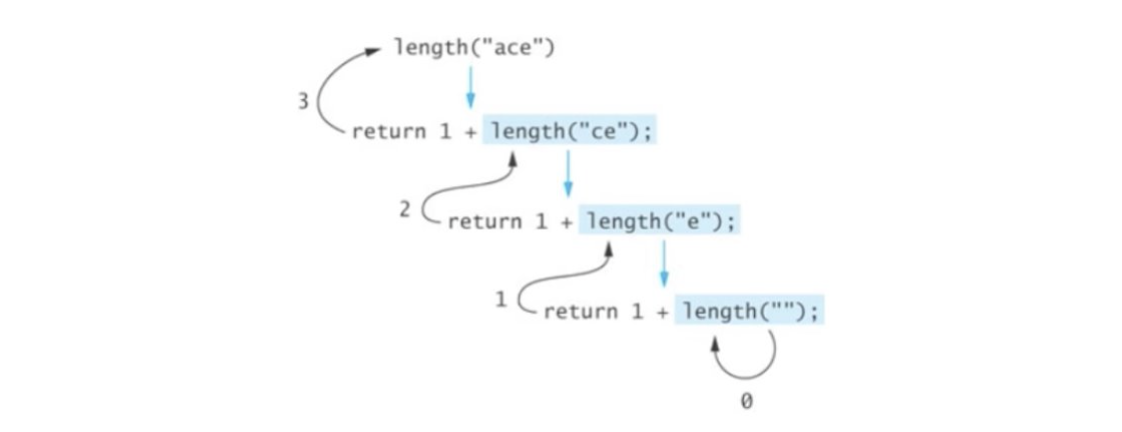
function strLength(str) {
  if (!str) {
    return 0
  } else {
    return 1 + strLength(str.substring(1))
  }
}

const str = "Hello world!"
strLength(str)

문자열의 프린트

function printChars(str) {
  if (!str) {
    return;
  } else {
    console.log(str.charAt(0))
    printChars(str.substring(1))
  }
}

const str = "Hello world!"
printChars(str)

문자열을 뒤집어 프린트

function printCharsReverse(str) {
  if (!str) {
    return;
  } else {
    printCharsReverse(str.substring(1))
    console.log(str.charAt())
  }
}

const str = "Hello world!"
printCharsReverse(str)

2진수로 변환하여 출력

function printInBinary(n) {
  if (n < 2) {
    console.log(n);
  } else {
    printInBinary(Math.floor(n / 2))
    console.log(n % 2);
  }
}
const n = 10;
printInBinary(n)

배열의 합 구하기

• data[0]에서 data[n-1]까지의 합을 구하여 반환

function arraySum(n, arr) {
  if (n <= 0) {
    return 0;
  } else {
    console.log(arr[n - 1]);
    return arr[n - 1] + arraySum(n - 1, arr)
  }
}

const n = 10;
const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
arraySum(n, arr);

Recursion Vs Iteration

재귀 vs 반복

• 모든 순환함수는 반복문으로 변경 가능
• 그 역도 성립함. 즉 모든 반복문은 recursion으로 표현 가능
• 순환함수는 복잡한 알고리즘을 단순하고 알기쉽게 표현하는 것을 가능하게 함
• 하지만 함수 호출에 따른 오버헤드가 있음(매개변수 전달, 액티베이션 프레임 생성 등)
• 함수가 중첩되어 호출되면 계속해서 메모리에 쌓여 stack overflow가 발생할 수 있음
• 성능면에서 뒤쳐질 수 있지만, 반복을 사용하면 굉장히 복잡할 수 있는 로직을 재귀로 단순화 할 수 있기 때문에 활용도가 높음

3. Designing Recursion

순환 알고리즘의 설계

무한루프에 빠지지 않는 재귀함수의 전제 조건

• 적어도 하나의 recursion에 빠지지 않는 경우가 존재해야 함
• recursion을 반복하다보면 결국 base case로 수렴해야 함

재귀함수 디자인

암시적(implicit) 매개변수를
명시적(explicit) 매개변수로 바꾸어라.

순차탐색

순차 탐색(반복) | Sequential search

• 이 함수의 mission은 data[0]에서 data[n-1]사이에서 target을 검색하는 것이다.
• 하지만 검색 구간의 시작 인덱스 0은 보통 생략한다. 즉 암시적 매개변수이다.
  ex)
  [0, n-1] => 0에서부터 n-1까지
  0 => 암시적
  n-1 => 명시적

function search(arr, n, target) {
  for (let i = 0; i < n; i++) {
    if (arr[i] === target) {
      return i
    }
  }
  return -1
}

const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
const n = 7
const target = 5
console.log(search(arr, n, target));

순차 탐색(재귀) | Sequential search

• 매개변수의 명시화
• 반복을 통한 순차 탐색에서 암시적 매개변수였던 시작점을 명시적으로 변경
  ex) 0 => start
  

function search(arr, begin, end, target) {
  if (begin > end) {
    return -1;
  } else if (target === arr[begin]) {
    return begin
  } else {
    return search(arr, begin + 1, end, target)
  }
}

const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
const begin = 0
const end = 7
const target = 5
console.log(search(arr, begin, end, target))

• 이 함수를 search(data, 0, n-1, target)으로 호출한다면
  반복문을 활용한 함수와 완전히 동일한 일을 함

  즉, 재귀함수를 구현할 때 처음 함수를 실행하는 경우뿐만 아니라 두번째, 세번째 실행할 때의 매개변수를 염두해두고 설계를 해야함

순차 탐색(재귀) v2

function search(arr, begin, end, target) {
  if (begin > end) {
    return -1;
  } else if (target === arr[end]) {
    return end
  } else {
    return search(arr, begin, end - 1, target)
  }
}

const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
const begin = 0
const end = 7
const target = 5
console.log(search(arr, begin, end, target));

순차 탐색(재귀) v3

function search(arr, begin, end, target) {
  if (begin > end) {
    return -1;
  } else {
    let mid = Math.floor((begin + end) / 2)
    if (arr[mid] === target) {
      return mid
    }
    let index = search(arr, begin, mid - 1, target)
    if (index !== -1) {
      return index
    } else {
      return search(arr, mid + 1, end, target)
    }
  }
}

const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
const begin = 0
const end = 7
const target = 5
console.log(search(arr, begin, end, target));

최대값 찾기

최대값 찾기(반복)

function findMax(arr) {
  let max = 0;
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] > max) {
      max = arr[i]
    }
  }
  return max
}
const arr = [1, 2, 5, 6, 4, 7, 9, 8, 3]
console.log(findMax(arr));

최대값 찾기(재귀)

• 반복문으로 구현한 최대값 찾기에서 암시적으로 표현한 0을 명시적으로 표현
  ex) 0 => index

function findMax(index, arr) {
  if (index === arr.length-1) {
    return arr[index]
  } else {
    return Math.max(arr[index], findMax(index + 1, arr))
  }
}
const arr = [1, 2, 5, 6, 4, 7, 9, 8, 3]
console.log(searchMaxValue(0, arr));

최대값 찾기(재귀) v2

function findMax(begin, end, arr) {
  if (begin === end) {
    return arr[begin]
  } else {
    let mid = Math.floor((begin + end) / 2)
    let max1 = findMax(begin, mid, arr)
    let max2 = findMax(mid + 1, end, arr)
    return Math.max(max1, max2)
  }
}
const arr = [1, 2, 5, 6, 4, 7, 9, 8, 3]
const end = arr.length - 1
console.log(findMax(0, end, arr));

이진 탐색 | Binary Search

• 조건 : 데이터가 크기 순으로 정렬되어 있음을 전제로 함
• arr[begin] ~ arr[end] 사이에서 target을 검색해서 index를 반환

function binarySearch(arr, target, begin, end) {
  if (begin > end) {
    return -1
  } else {
    let mid = Math.floor((begin + end) / 2)
    if (arr[mid] === target) {
      return mid
    } else if (arr[mid] > target) {
      return binarySearch(arr, target, begin, mid - 1)
    } else {
      return binarySearch(arr, target, mid + 1, end)
    }
  }
}

//if arr가 정렬되어 있지 않다면, arr.sort() 필요
const arr = [1, 2, 4, 9, 13, 15, 20, 22, 30, 40, 50, 60, 77, 100];
const target = 77;
const begin = 0;
const end = arr.length - 1; 
console.log(binarySearch(arr, target, begin, end));

📚 참고

YOUTUBE | 2015 봄학기 알고리즘 | 권오흠
모던 JavaScript 튜토리얼 | 재귀와 스택

---

Photo by Michael Dziedzic on Unsplash