알고리즘 16 그래프 | DAG | JS

3. 방향 그래프 | Directed Acyclic Graph(DAG)

• Acyclic. 즉, cycle이 존재하지 않는 그래프
  

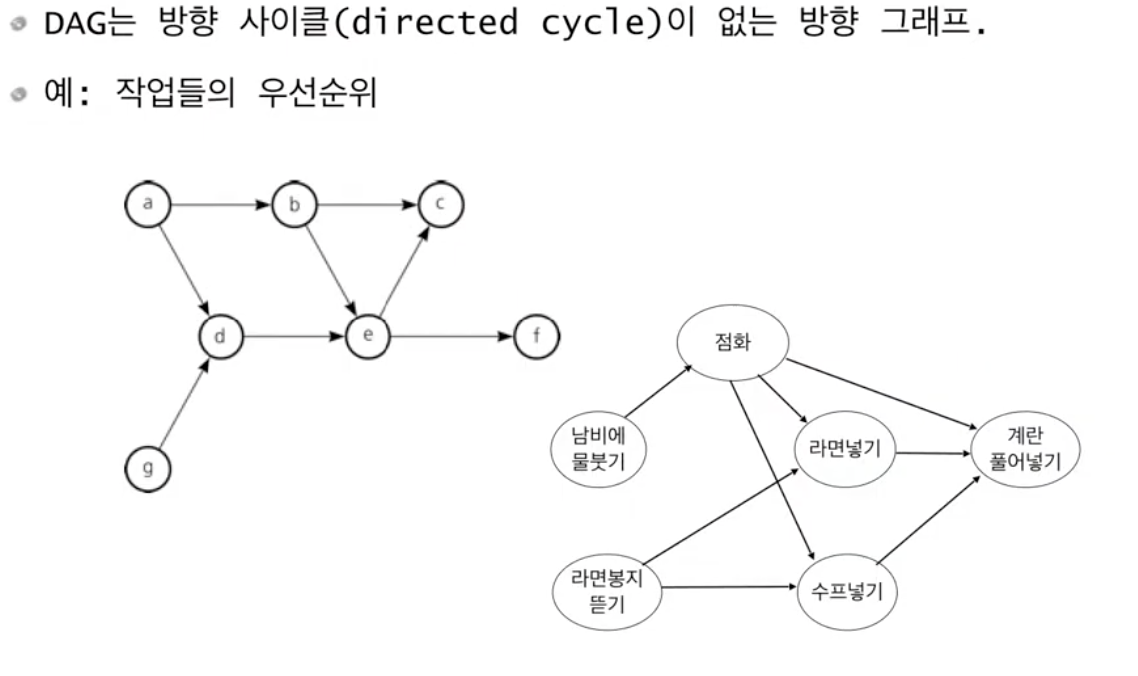
위상정렬(1) | topological ordering

*일반적으로 위상정렬의 해는 유일하지 않음

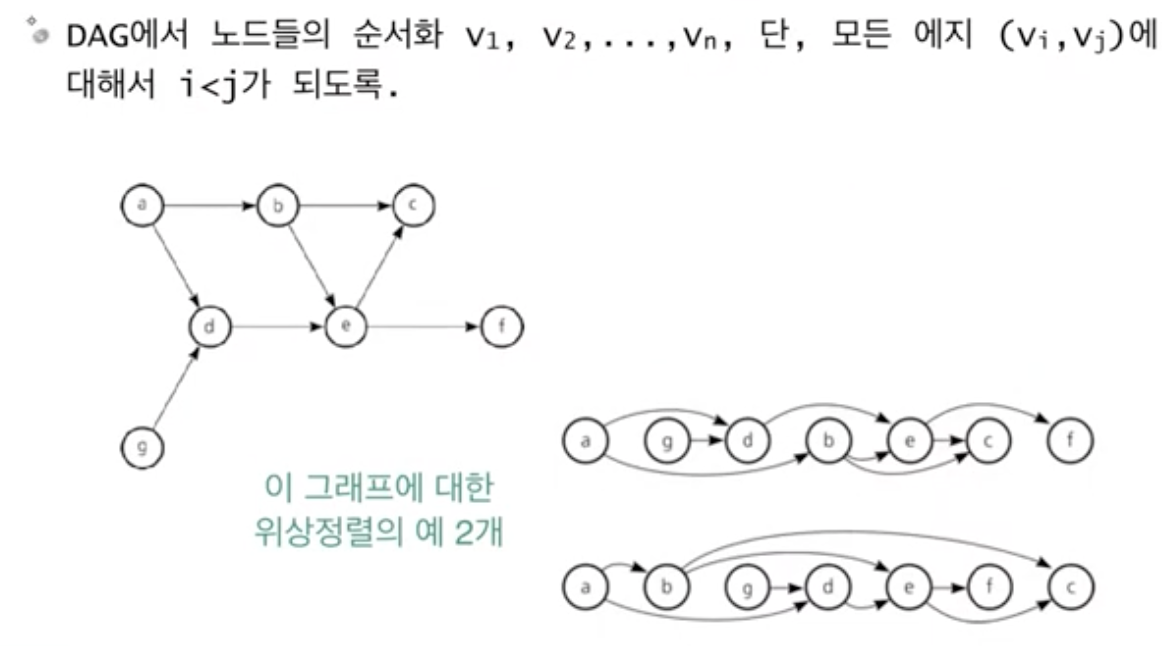
• incoming Edge(진입간선) = 들어오는 엣지 / outgoing Edge(진출간선) = 나가는 엣지
• indegree = 들어오는 edge 갯수 / outdegree = 나가는 edge 갯수
  *indegree가 0인 노드는 선행하는 작업이 없다는 의미

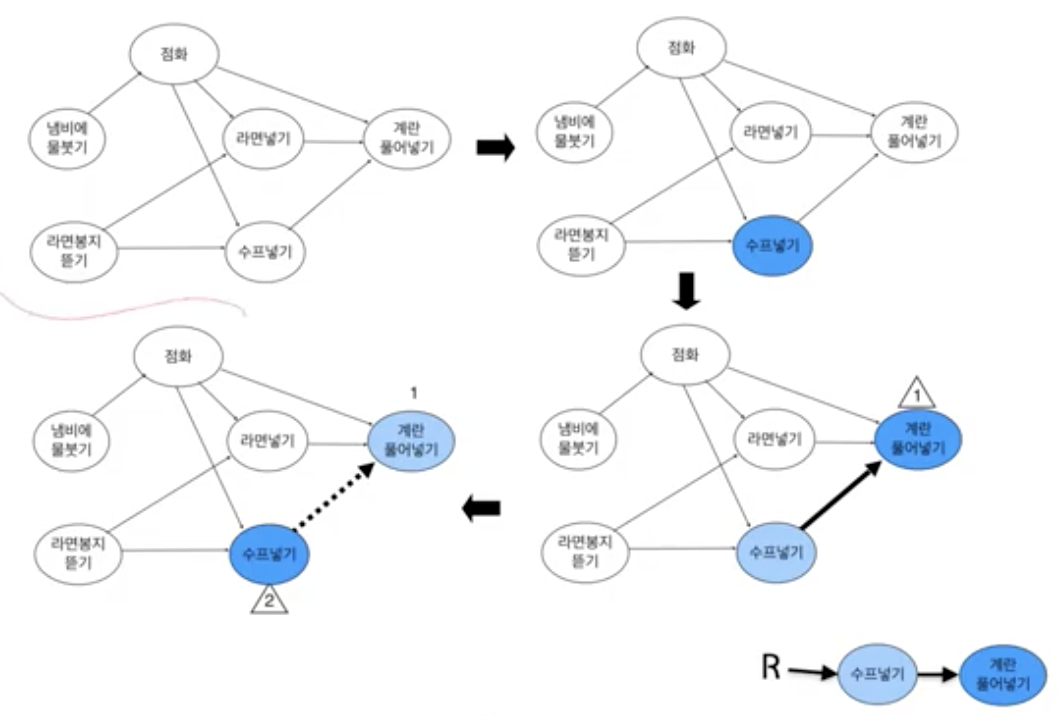
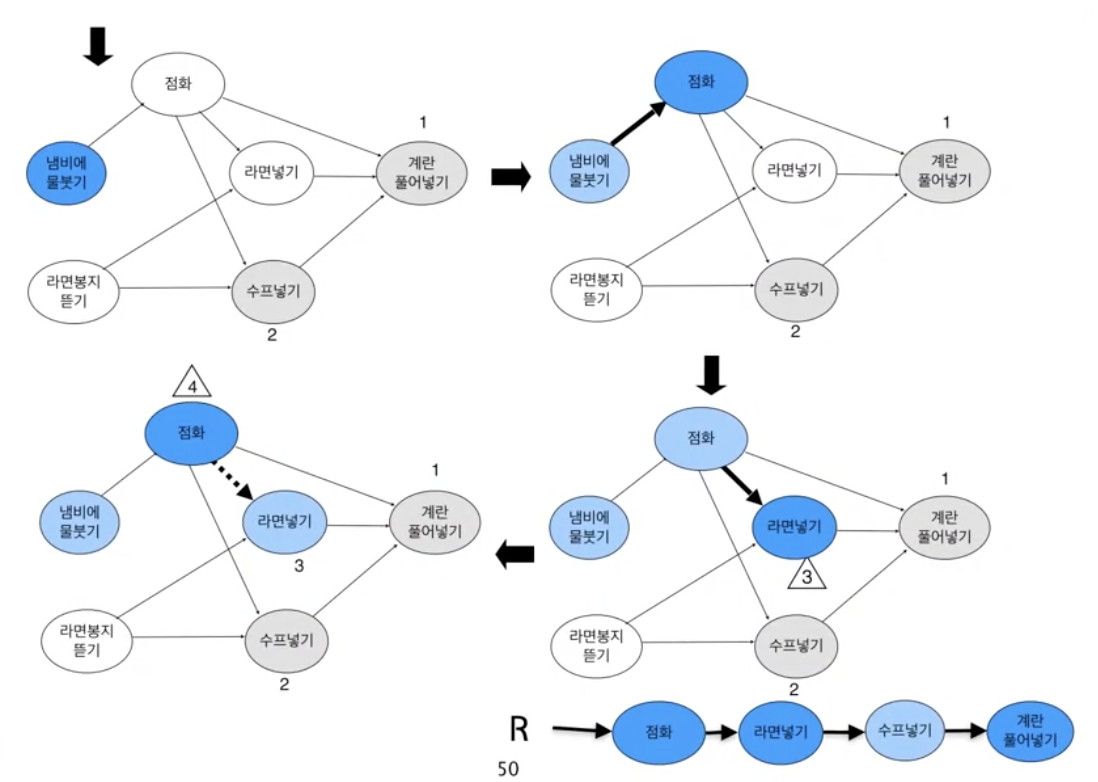
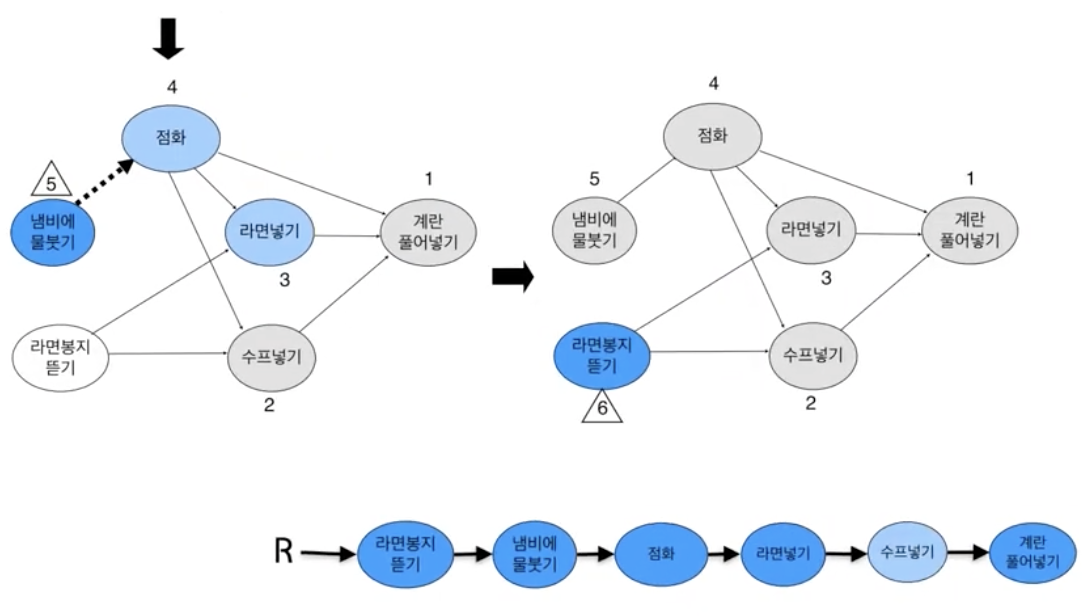
1. indegree가 0인 노드 u를 선택
2. result에 넣음
3. u와 u의 진출 간선을 모두 제거
4. 1~3을 반복

위상정렬(2) | topological ordering

📚 참고

YOUTUBE | 2015 봄학기 알고리즘 | 권오흠

Photo by Michael Dziedzic on Unsplash