youtube link

Beta Distribution

비율을 설명할 때 사용하는 분포
ex) 불순률, 불량률 등

$X$ : beta random variable with parameter $\alpha$ and $\beta$
the pdf of $X$ :

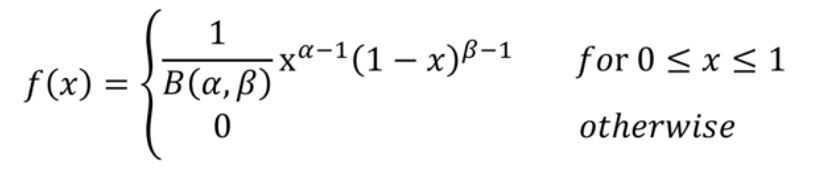
x = 랜덤변수 값, $\alpha,\ \beta$ = parameter

내가 궁금한 건 이 분포를 어디에 쓰냐, 어떤 상황을 이 분포로 모사한 것인가?
고장률은 초반에 고장이 많고 유지가 되다가 수명이 다되면 고장률이 올라가는 분포를 따른다

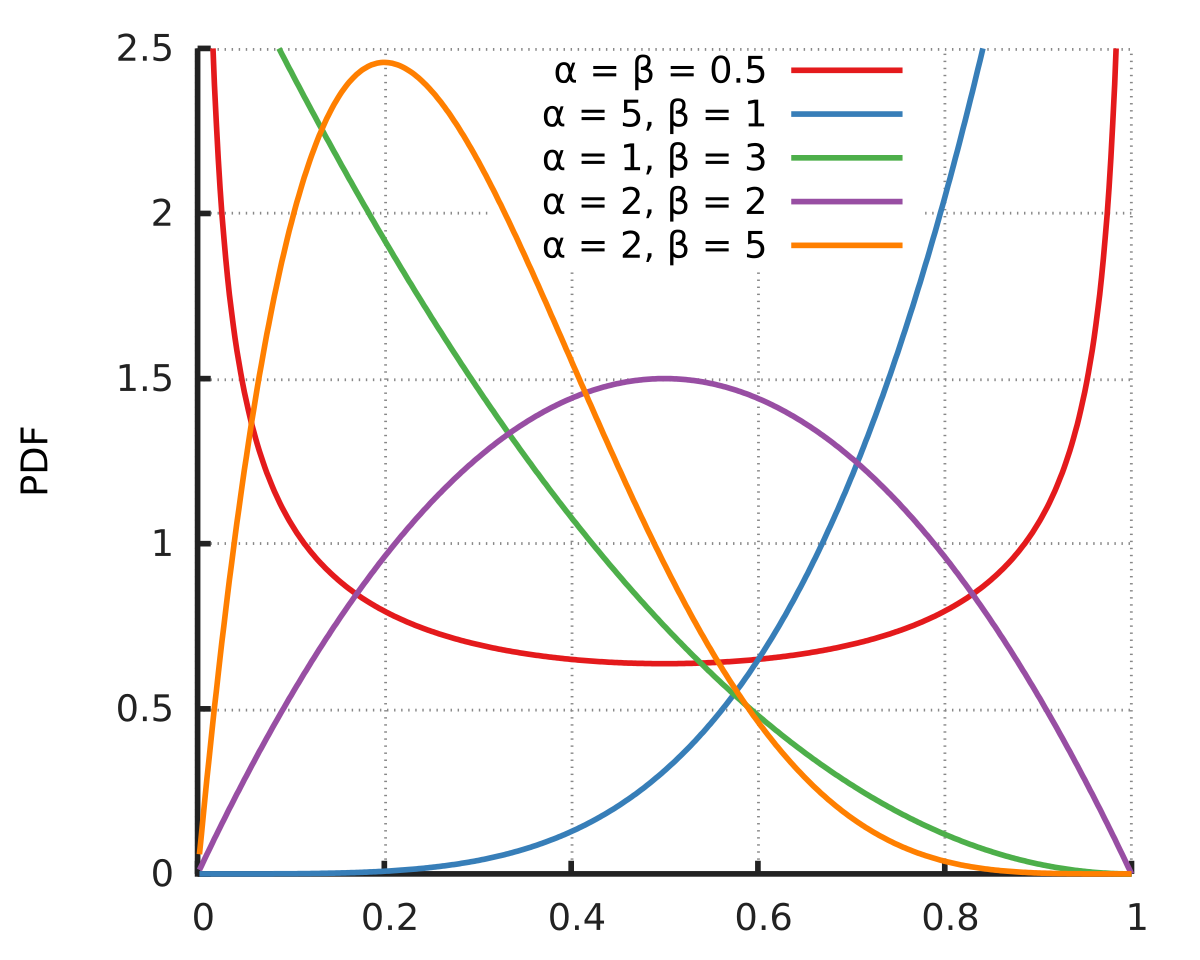
예시

여왕벌이 새로운 벌집을 만들기 위해 무리를 떠날 때, 일부 벌들이 여왕벌을 따라간다.
일벌들이 여왕벌을 따라가는 비율을 beta distribution으로 설명할 수 있다.
$\alpha=2$, $\beta=4.8$
절반 이상의 벌이 여왕벌을 따라갈 확률은?

$X$ = 여왕벌을 따라가는 일벌들의 비율

$P(X>0.5)=\int^1_0.5{1\over B(2, 4.8)} x^1(1-x)^{3.8}dx$

정리하면 주로 어떤 비율을 의미하는 random variable의 분포를 베타 분포로 나타낸다
베타분포를 이항분포의 continuous 버전이라고 말할 수도 있다

Dirichlet Distribution

Beta Distribution을 다항분포 형태로 확장시킨 것이 Dirichlet Distribution이다

예를 들면
Beta Distribution에서는 일벌이 여왕벌을 따라가는지 아닌지에 대한 둘 중 하나를 고르는 비율이었다면
Dirichlet Distribution은 가위바위보에서 가위를 낼지 바위를 낼지 보를 낼지에 대한 확률이라고 생각할 수 있다

그러니까 (0.5, 0.3, 0.2), (0, 1, 1)와 같은 값들을 표본으로 가질 수 있다
이 때의 k값은 3이다

$Dir(p_1, p_2, ... p_k; \alpha_1, \alpha_2, ..., \alpha_k) = Dir(P;\alpha)$
이 때, $\alpha$는 Dirichlet 분포의 hyperparmeter vector

그리고 이렇게 생겼다
$Dir(x;\alpha) = {1\over B(\alpha_1, \alpha_2, ... \alpha_K)}\prod^K_{i=1}x^{\alpha_i-1}_i$