배열로 이진트리 표현하기
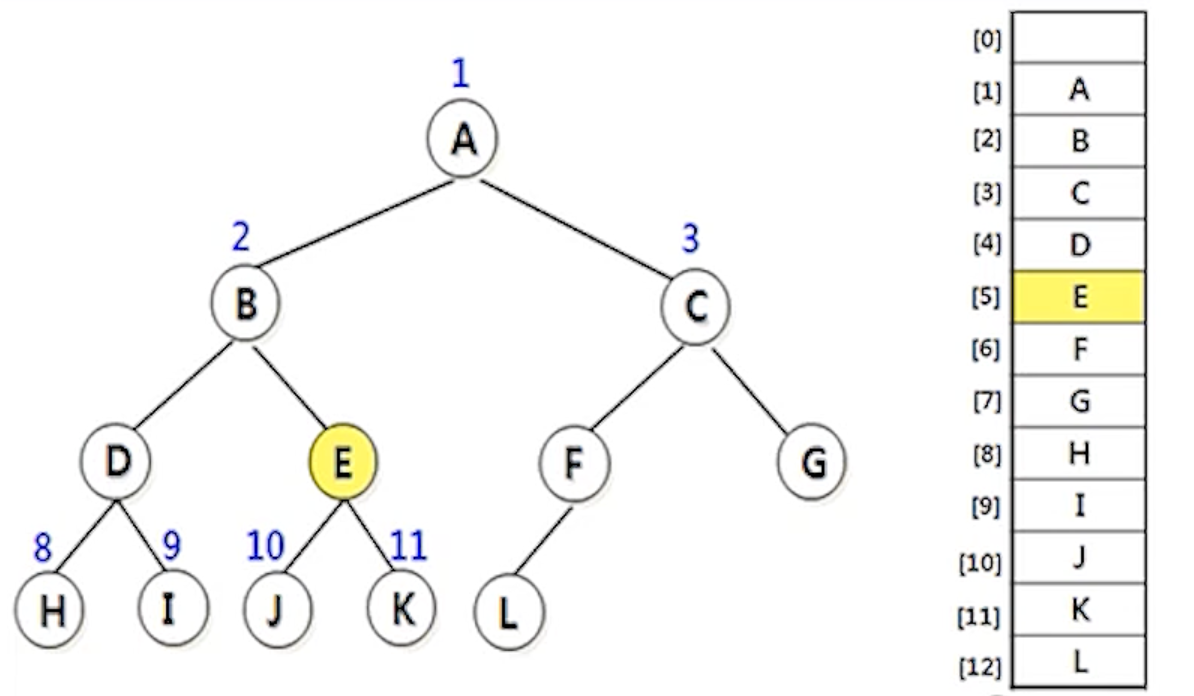
트리를 표현하기 위해 배열을 사용하면
실제 트리에서 비어있는 부분도 전부 인덱스로 설정함
쓰지 않는 인덱스들은 결국 빈값이 되기 때문에 메모리가 낭비되지만
구현이 쉽기 때문에 배열로 이진트리를 구현해도 괜찮음
참고로 이렇게 되면 이진트리 노드가 N이라면 배열로 생성하면 그 시간복잡도는 O(N)
이진트리 순회하기
순회 = 빠짐없이 노드들의 데이터를 방문하는 것
아래에 대표적인 3가지 방식의 순회 방법을 소개하는데
이때 중요한 것은 현재 노드를 부모노드로 생각했을 때!!
전위순회 Preorder
부모 ->왼쪽자식 -> 오른쪽 자식
직관적으로 가장 이해하기 쉬운 순회 방식으로 트리를 복사할 때에 많이 사용함
중위순회 Inorder
왼쪽자식 -> 부모 -> 오늘쪽 자식
현재 노드를 거치기만 할 뿐 방문하지는 않음!
후위순회 Postorder
왼쪽자식 -> 오른쪽 자식 -> 부모
노드를 삭제할 때 부모 먼저 삭제할 수 없기 때문에 트리를 삭제할때 후위 순회가 주로 사용됨
Pointer로 표현하기
하나의 노드를 구현할 때 서로의 관계를 표현함
그러니까 노드가 노드의 값 + 왼쪽 자식노드 + 오른쪽 자식노드 로 표현됨
그렇기 때문에 메모리 공간을 낭비하진 않지만
노드를 하나하나 따라가도록 구현해야하기 때문에 구현 난이도가 높음
여기까지 기초라고 하면
이진 트리에서 가장 중요한 것은 탐색이 효율적이어야 한다는 것
그러니까 여기저기 왓다갓다 값찾는게 효율적이도록 트리를 구축하는 것이 가장 중요함!!
이진 탐색 트리
binary search tree라고 하고 이를 활용해 원하는 노드를 효율적으로 찾아보자
예를 들어 트리의 데이터가 아래의 순서대로 들어온다
3 -> 4 -> 2 -> 8 -> 9 -> 7 -> 1
이진 탐색트리는 데이터 크기가 작으면 왼쪽 자식
크거나 같으면 오른쪽 자식 위치에 배치한다
이게 무슨말이냐면
오른쪽 자식들은 나를 기준으로 전부 다 크거나 같고
왼쪽 자식들은 나를 기준으로 전부 다 작다
(대대손손!)
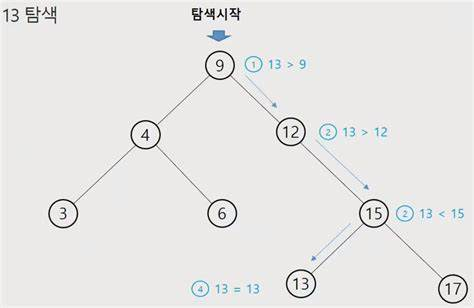
이런 식으로!
규칙이 있으니까 이 규칙을 기반으로 탐색하면 됨
이미지에서 처럼 내가 찾으려는 값이 13이라면
찾으려는 값이 현재노드보다 크면 오른쪽 작으면 왼쪽 이렇게 움직인다
이런 방식이 검색을 빠르게 만들어 줌
예를 들어 위의 이진트리에서 배열 방식이었다면?
[3, 4, 6, 9, 12, 13, 15, 17]
여기서 13을 찾기위해 6번의 비교연산을 수행해야함! (13의 배열 위치까지!)
하지만 트리 기반으로 탐색하면 4번의 비교연산으로 13을 찾아낼 수 있음
그럼 당연히 이 시간 복잡도는 트리가 얼마나 균형잡히게 생겼는지에 의존함
잘 균형이 잡혀있다면 삽입과 탐색 연산시 저장된 노드가 N개라고 할 때
시간복잡도는 O(logN) 임!!
하지만 완저니 치우쳐저 있다면? 당연히 배열이랑 똑같은 O(N)임!
이런 치우쳐진 형태를 degenerate binary tree라고 표현함
균형 이진 탐색 트리 balanced binary search tree
세부적으로는 AVL 트리, 레드-블랙 트리 이렇게 구분하기도 하는데
사실 완전히 균형적인 이진 탐색 트리는 구현 난이도가 높아서
더 공부하고 싶으면 따로 깊게 파야함
문제 26. 트리 순회
## question 26
def preorder(nodes, idx=0):
if idx < len(nodes):
traj = str(nodes[idx]) + " "
traj += preorder(nodes, idx * 2 + 1)
traj += preorder(nodes, idx * 2 + 2)
return traj
else:
return ""
def inorder(nodes, idx=0):
if idx < len(nodes):
traj = inorder(nodes, 2 * idx + 1)
traj += str(nodes[idx]) + " "
traj += inorder(nodes, 2 * idx + 2)
return traj
else:
return ""
def postorder(nodes, idx=0):
if idx < len(nodes):
traj = postorder(nodes, 2 * idx + 1)
traj += postorder(nodes, 2 * idx + 2)
traj += str(nodes[idx]) + " "
return traj
else:
return ""
def solution(nodes):
return [preorder(nodes)[:-1], inorder(nodes)[:-1], postorder(nodes)[:-1]]
nodes = [1, 2, 3, 4, 5, 6, 7]
print(solution(nodes))이거 거의 답지보고 했음;;
재귀가 들어가면 어쩔줄 몰라하는 나~~
일단 시간 복잡도가 몇일까?
모든 노드를 방문하기 때문에 일단 O(N)
문제 27. 이진 탐색 트리 구현
pointer 방식으로 이진트리 구현..
이것도 답지보고했음;;
## question 27
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, key):
if not self.root:
self.root = Node(key)
else:
curr = self.root
while True:
if key < curr.val:
if curr.left:
curr = curr.left
else:
curr.left = Node(key)
break
else:
if curr.right:
curr = curr.right
else:
curr.right = Node(key)
break
def search(self, key):
curr = self.root
while curr and curr.val != key:
if key < curr.val:
curr = curr.left
else:
curr = curr.right
return curr
def solution(lst, search_lst):
bst = BinarySearchTree()
for key in lst:
bst.insert(key)
result = []
for key in search_lst:
if bst.search(key):
result.append(True)
else:
result.append(False)
return result
lst = [5, 3, 8, 4, 2, 1, 7, 10]
lst_tree = [5, 3, 8, 2, 4, 7, 10, 1]
search_lst = [1, 2, 5, 6]
print(solution(lst, search_lst))문제 28. 예상 대진표
하 돌겟네 트리!!
## question 28
def solution(N, A, B):
answer = 0
while A != B:
A = (A + 1) // 2
B = (B + 1) // 2
answer += 1
return answer
N = 8
A = 4
B = 7
answer = 3
solution(N, A, B)문제 29. 다단계 칫솔 판매
내가 한 것 :
## question 29
from math import floor
def solution(enroll, referral, seller, amount):
# 조직도와 수입 초기화
organize = {}
income = {}
for i in range(len(enroll)):
if enroll[i] in organize:
organize[enroll[i]] = referral[i]
income[enroll[i]] = 0
for i in range(len(seller)):
money = amount[i] * 100
p = seller[i]
while p != "-":
income[p] += (money - floor(money * 0.1))
money = floor(money * 0.1)
p = organize[p]
return list(income.values())
enroll = ["john", "mary", "edward", "sam", "emily", "jaimie", "tod", "young"]
referral = ["-", "-", "mary", "edward", "mary", "mary", "jaimie", "edward"]
seller = ["young", "john", "tod", "emily", "mary"]
amount = [12, 4, 2, 5, 10]
result = [360, 958, 108, 0, 450, 18, 180, 1080]
print(solution(enroll, referral, seller, amount))내가 몰랐던 것 :
여기서 enroll이랑 referral이랑 짝지을때,
나는 for문으로 일일이 돌리면서 했는데 zip으로 묶어줄 수 있음!
그러니까organize = dict(zip(enroll, referral)) income = {name : 0 for name in enroll}이렇게 하면 훨씬 간단하게 할 수 있었음!!
비슷하게 마지막에도 list할때 순서 바뀔까봐 불안했는데,
[income[name] for name in enroll]했으면 해결될 일!
너비 우선 탐색
start - end 까지의 경로를 찾는 문제는
대표적으로 BFS와 DFS를 많이 말한다
그리고 그 길에 가중치가 있다면 다익스트라 알고리즘이라는 것도 있음!
여기서 다음에 나올 예제가 미로탐색이라서
너비 우선 탐색에 대해 잠깐 짚고 넘어가고자 한다
너비 우선 탐색은 항상 최단 경로를 보장한다!
모든 가능한 길에 대해서 다 훑어보고 가장 먼저 끝나는걸 get하면 되기 때문!
쉽게 생각하면 너비우선은 10문제를 풀기위해 5초하고 다음문제 5초하고 다음문제 이런식이면
깊이 우선은 1문제 결과 나올때까지 풀고 다음문제 넘어가는 식!
문제 30. 미로 탈출
내가 풀이를 보고 이해한 바로는
가능한 병사들을 무한히 세팅해놓고
갈림길이 나올때마다 병사를 풀어서
그 병사들의 GPS를 추적하는 방식!
내가 답지를 본 후에
아이디어 이해하고 다시 짠 것 :
## question 30
from collections import deque
def solution(maps):
q = deque()
dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]
n = len(maps[0])# 가로
m = len(maps)# 세로
visited = [[[0] * 2 for _ in range(n)] for _ in range(m)]
# start 파악하기
find_start = False
for i in range(n):
if find_start:
break
for j in range(m):
if maps[j][i] == 'S':
start_x = i
start_y = j
q.append([start_x, start_y, 0, 0]) # x좌표, y좌표, lever작동여부, time
visited[j][i][0] = 1
find_start = True
break
# 경로 탐색하기
while q:
x, y, l, time = q.popleft()
for k in range(4):
new_x = x + dx[k]
new_y = y + dy[k]
if (0 <= new_x < n) and (0 <= new_y < m) and (visited[new_y][new_x][l] != 1):
if (maps[new_y][new_x]=='E') and (l==1):
return time + 1
elif maps[new_y][new_x] == 'O' or maps[new_y][new_x] == 'S':
q.append([new_x, new_y, l, time + 1])
visited[new_y][new_x][l] = 1
elif maps[new_y][new_x] == 'L':
q.append([new_x, new_y, 1, time + 1])
visited[new_y][new_x][0] = 1
visited[new_y][new_x][1] = 1
elif (maps[new_y][new_x]=='E') and (l==0):
q.append([new_x, new_y, l, time + 1])
visited[new_y][new_x][l] = 1
return -1