CNN 첫걸음

Convolution 연산 이해하기

• Convolution 연산은 Kernel을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
  
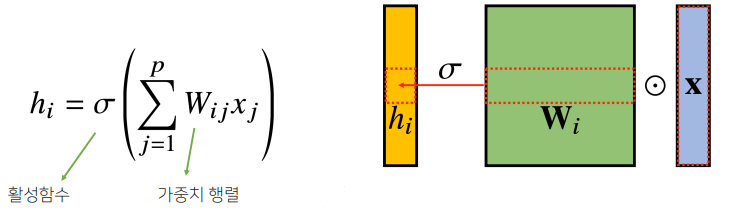
  - 고정된 커널을 입력벡터 상에서 움직여가면서 계산 적용
  - 활성화 함수를 제외한 Convolution 연산도 선형변환에 속함
  - kernel이 공통적으로 적용되기 때문에, parameter size 줄일 수 있음
  
• Convolution 연산의 수학적인 의미는 신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것
  
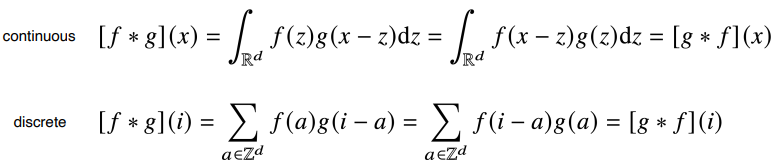
  - CNN에서 사용하는 연산은 사실 convolution이 아니라 cross-correlation
  - 위의 식에서 -로 되어있는 부분 +로도 변환 가능
  
• 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용
  
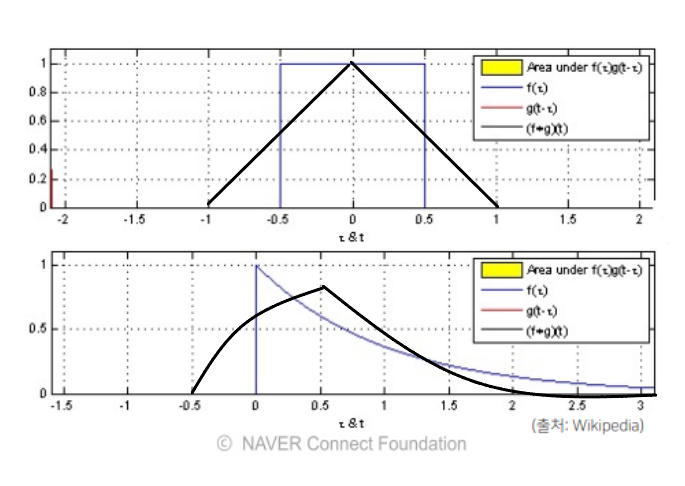
  - 커널(빨간색) 움직여가면서 연산(파란색)에 적용될 때 국소적으로 적용되는 연산(노란색 박스)의 결과가 검은색 그래프

다양한 차원에서의 Convolution

• 데이터의 성격에 따라 사용하는 커널이 달라짐
  
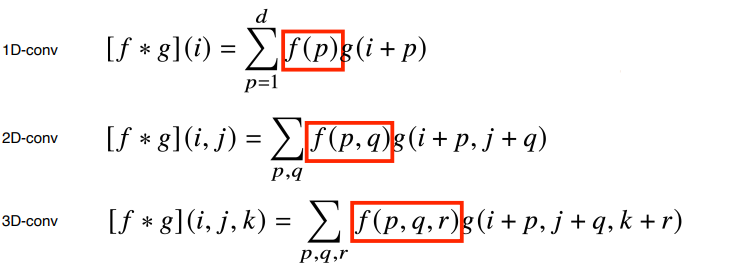
  - 1차원-conv : 한 변수에 대해 좌우로 움직임 (음성, 테스트)
  - 2차원-conv : 두 개의 좌표계에서 상하좌우로 움직임 (사진)
  - 3차원-conv : 세 개의 좌표계에서 상하좌우+앞뒤로 사용 (영상)

2차원 Convolution 연산 이해하기

• 2D-Conv 연산은 kernel을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용됨
  
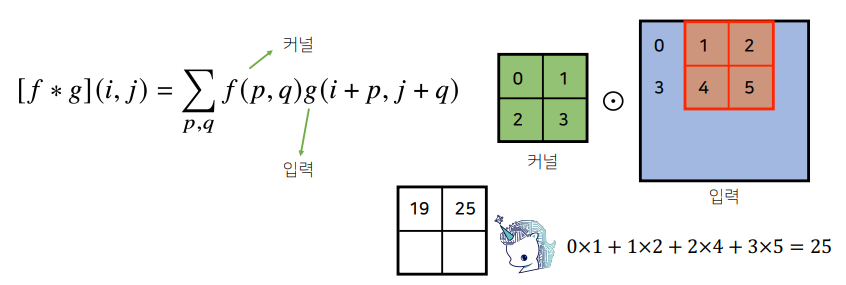
  - i, j는 고정. p, q로 이동
  - 커널과 입력벡터 간 성분곱 수행
  
• 입력 크기를 (H, W), 커널 크기를(K_H, K_W), 출력 크기를 (O_H, O_W)라 할 때 출력 크기는
  
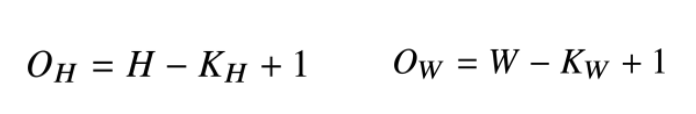
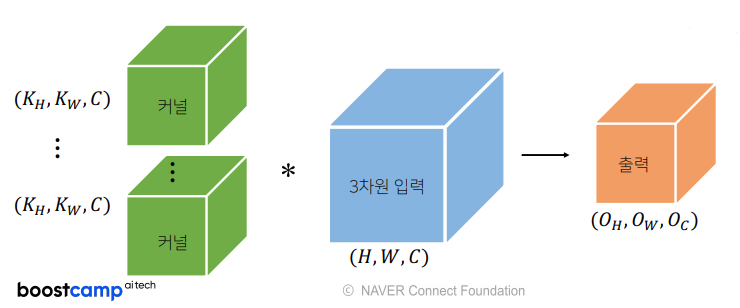
• 채널이 여러개인 2차원 입력의 경우, 2차원 Convolution을 채널 개수만큼 적용
  - 채널이 여러개인 경우, 커널의 채널 수와 입력의 채널 수가 같아야
  

Convolution 연산의 역전파 이해하기

• Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나옴
  
  
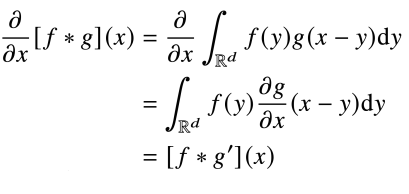
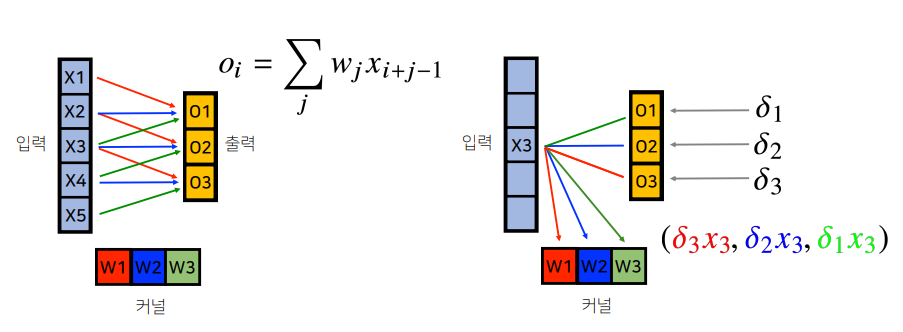
  - X3 -> (O₁, O₂, O₃)에 적용되는 가중치에 따라 gradient vector에 연결되는 가중치 결정됨
  
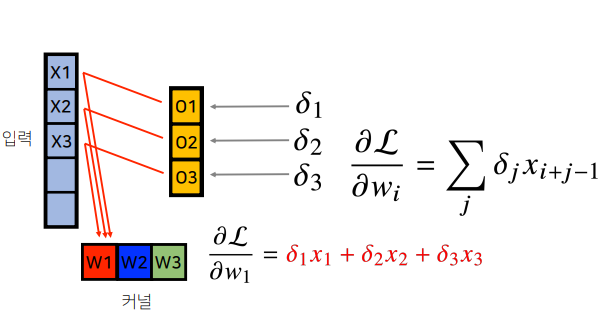
  - 각 커널에 들어오는 모든 그레디언트를 더하면 결국 convolution 연산과 같음