확률론 맛보기

딥러닝에서의 확률론?

• 딥러닝은 확률론 기반의 기계학습 이론에 바탕
• 기계학습에서의 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도 - 예측이 틀릴 위험을 최소화하기 위해
• 회귀 분속에서 손실함수로 사용되는 L2-norm은 예측오차의 분산을 가장 최소화하는 방향으로 학습
• 분류 문제에서 사용되는 교차 엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습
• 분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 잘 선택해야 함

이산확률변수 vs 연속확률변수

• 확률변수는 확률분포 D에 따라 이산형(discrete)과 연속형(continous) 확률변수로 구분
  

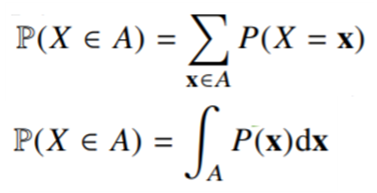
이산형 확률변수

• 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링 수행
• 일반 컴퓨터에서 가장 많이 사용

연속형 확률변수

• 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링 수행
  - 밀도는 누적확률분포의 변화율을 모델링. 확률이 X
• 기계학습에서 자주 사용
  

확률분포는 데이터의 초상화

• 데이터공간을 X * Y로 표기하고, D는 데이터공간에서 데이터를 추출하는 분포
  
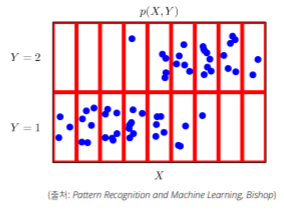
• (x, y) ∈ X * Y는 데이터 공간 상의 관측 가능한 데이터 (위의 사진에서의 파란색 점)
• 확률분포에 따라 모델링 방식에 달라짐
  - 어떤 식으로 data 접근하냐에 따라 분포의 성질 달라짐
  • 분포의 종류에 따라 확률분포 modeling 방법 달라짐
• P(x)는 입력 x에 대한 주변확률분포로 y에 대한 정보를 주진 않음
  
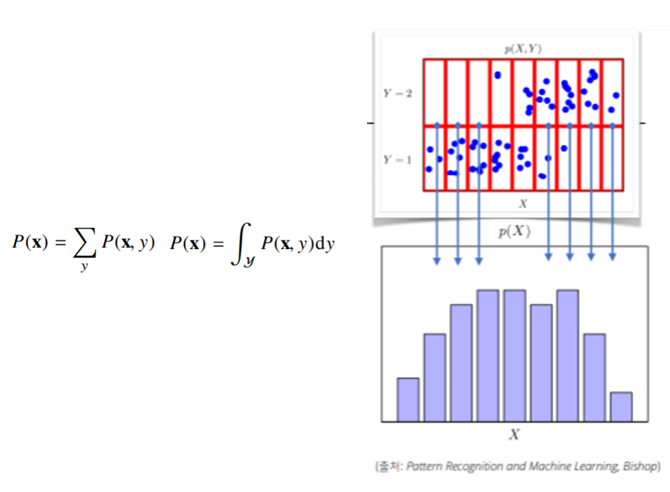
  - 아래의 그래프는 각 X의 값에 따른 빈도를 나타냄 (Y의 값과 연관 X)
• 조건부확률분포 P(x|y)는 데이터 공간에서 입력 x와 출력 y 사이의 관계를 모델링
  
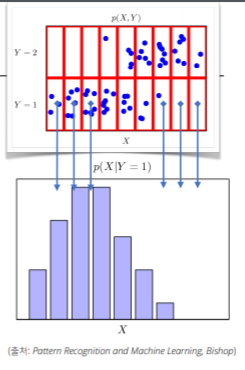
  - P(x|y)는 특정 클래스가 주어진 조건에서 데이터의 확률분포를 보여줌
  - 주어진 class에 대해 정보가 각각 어떤 식으로 되어있는가 확인할 때 사용
  

조건부확률과 기계학습

• 조건부확률 P(x|y)는 입력변수 x에 대해 정답이 y일 확률
• 로지스틱 회귀에서 사용하는 선형모델과 softmax 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는 데 사용
• 분류 문제에서 softmax(W∮+b)은 데이터 x로부터 추출된 특징패턴 ∮(x)와 가중치행렬 W를 통해 조건부확률 P(y|x) 계산
• 회귀 문제의 경우 조건부기대값 E[y|x] 추정
  - 조건부기대값은 L2-norm(E||y-f(x)||)를 최소화하는 함수 f(x)와 일치
• 딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴 ∮ 추출

기대값 (expectation)

• 기대값은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는 데 사용
  
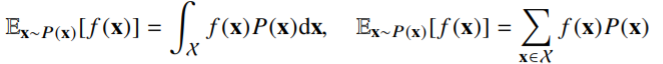
  - 연속확률분포의 경우엔 적분, 이산확률분포의 경우엔 급수 사용
• 기대값을 이용해 분산, 첨도, 공분산 등 여러 통계량 계산 가능

몬테카를로 (Monte Carlo) 샘플링

• 확률분포를 모를 때 데이터를 이용하여 기대값을 계산하기 위한 방법
  
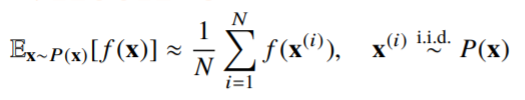
• 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙에 의해 수렴성을 보장