RSA

---

RSA 공개키 암호화 방식은 지속적으로 많이 쓰이고 있는 방식입니다.
상당히 다양한 분야에서 가장 많이 쓰이고 있는 공개키 암호화 방식이기 때문에 이해하고 있다면 좋은 분야 입니다.

RSA는 큰 수는 소인수 분해를 하기 어렵다는 방식을 기반으로 암호화된 문장이 복호화 되기 어려운 것을 가정으로 하고 진행합니다.

여러 암호학, 수학 공식이 그렇듯 RSA 역시 만드신 분의 이름에서 따온 약자입니다.

자세한 계산 방식보다는 코드를 통한 구현을 위주로 설명하겠습니다. 정수론에 대한 기본지식이 조금 필요합니다.

How Work

---

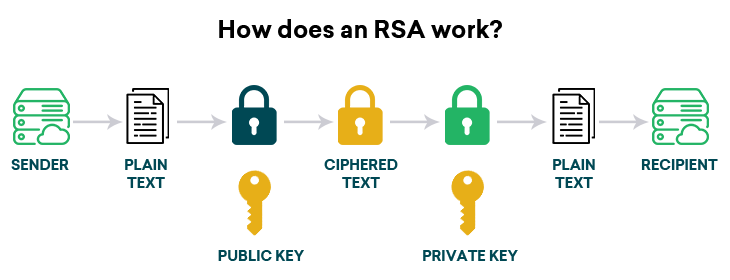
위 사진에 나와 있듯이 text(메시지)를 전송할 때 공개키로 암호화 하고 받는 수신자가 개인 키(복호화 키)를 이용해 복호화하는 방식입니다. 이는 많은 공개 키 암호화 방식의 로직과 같습니다.

• a: 메시지(sender가 전송)
• q,p: 큰 소수 2개
• m = q*p (공개 키)
• k: φ(m)과 서로소인 숫자(공개 키)

  φ(m): m보다 작은 m과 서로소인 정수를 의미합니다.
  φ(m) = φ(p)φ(q) = (p − 1)(q − 1)

q,p는 절대로 남에게 공개되지 않아야 하며 1024bits 이상의 수가 사용되어야 합니다. 이유는 일정 시간 내에 공격자가 q,p 값을 알게 된다면 밑에서 설명할 암호문 복호화가 가능해지기 때문입니다.

위에서 언급했듯이 RSA는 큰수의 소인수 분해 알고리즘이 복잡하고 시간이 오래 걸린다는 것을 가정으로 하고 있기 때문에 여기서 m 값을 소인수 분해한 값인 q,p는 남들에게는 공개되어서는 안될 소중한 값들 입니다.

암호화

---

암호화는 아래의 공식을 기반으로 이뤄지게 됩니다.

a^k ≡ b (mod m)

• 여기서 b는 암호화된 메시지 입니다.

암호화된 메시지를 구할 수 있는 간단한 코드입니다.

pow(a,k,m) # pow는 a의 k승을 m으로 모듈러 연산을 수행합니다.

이렇듯 공개키 k,m을 이용해 메시지 a를 b로 암호화할 수 있습니다.

복호화

---

복호화는 암호화된 문장을 다시 평문으로 바꾸는 과정입니다.
복호화 공식은 아래와 같습니다.

x^k ≡ b (mod m)

여기서 저희가 구해야 할 값은 x입니다.

step1. φ(m)

우선 오일러 공식을 사용해 m보다 작은 m과 서로소인 숫자들의 개수를 구해야 합니다.

φ(m) = φ(p)φ(q) = (p − 1)(q − 1)

위 공식과 같기 때문에 당연히 q,p를 알고 있는 사람은 바로 구할 수 있을 것 입니다.
하지만 모른다면 일일히 개수를 카운트해야 합니다.

def euler_phi(n):
    result = 1  # 1은 모든 n과 서로소
    for i in range(2, n):
        if gcd(n, i) == 1:
            result += 1
    return result

보시면 최대 공약수가 1인 숫자들을 일일히 카운트 하고 있습니다.

def gcd(a, b): # 최대 공약수 반환
    while b != 0:
        a, b = b, a % b
    return a

step 2. 역원(비밀 키 계산)

k (mod φ(m)) 에 대한 역원을 구해야 합니다.
이 말은 곧 비밀키 u에 대한 역원을 찾는 것 입니다.
ku ≡ 1 (mod φ(m))

위 공식에서 u를 찾기 위해서는 k의 역원이 필요합니다. 확장된 유클리드 알고리즘을 통해 구할 수 있습니다.

확장된 유클리드 알고리즘(계산 과정에 대해서는 나중에 글을 다시 작성하도록 하겠습니다.)

def EEA(r1, r2, u1, u2, v1, v2) :
    if r2 == 0:
        print(f'gcd: {r1}\nx: {u1}\ny: {v1}')
        return
    q = r1//r2
    r = r1%r2
    u = u1 - q*u2
    v = v1 - q*v2

    return EEA(r2, r, u2, u, v2, v)

만약 공개 키 k가 5라면 아래와 같이 확장된 유클리드 알고리즘을 사용할 수 있습니다.

# 복호화 복호화 키(d) == 비밀키 == 개인키 를 찾기 위해 역원 계산
print(EEA(5,euler_phi(91),1,0,0,1))

실행하게 되면 3가지 값이 반환되는데요

• gcd: 1
• x: 29
• y: -2

여기서 중요한 값은 바로 x 값입니다. x 값이 만약 양수라면 바로 비밀키 u의 역원으로 생각해도 되지만 만약 음수라면 양수로 만들어 주기 위해 x (mod m)을 다시 한번 계산한 값을 역원으로 사용하면 됩니다.

이렇게 찾은 역원을

ku ≡ 1 (mod φ(m)) 의 양변에 곱해주면 아래와 같은 식이 도출됩니다.
u ≡ k^-1 * 1 (modφ(m))

비밀 키를 이용한 복호화

이제 위 식을 이용해 비밀키 u을 구했다면

b^u mod m

• b: 암호문
• u: 개인키
• m : q*p 공개 키

위 식에 각 요소를 대입해 계산하게 되면 평문이 나오게 됩니다.

이렇듯 RSA 공개키 암호화 방식은 m 값을 소인수 분해한 q,p 값을 찾는게 어렵다는 전제하에 진행되게 됩니다.
(q,p 값 구하지 못한다면 위 python 코드처럼 일일히 계산해야 합니다.)

오늘은 간단한 코드로 구현해서 결과를 도출하는 과정에 대해서만 알아봤습니다.
저도 정수론과 함께 암호학에 대한 더 깊은 공부가 필요한 것 같습니다...!