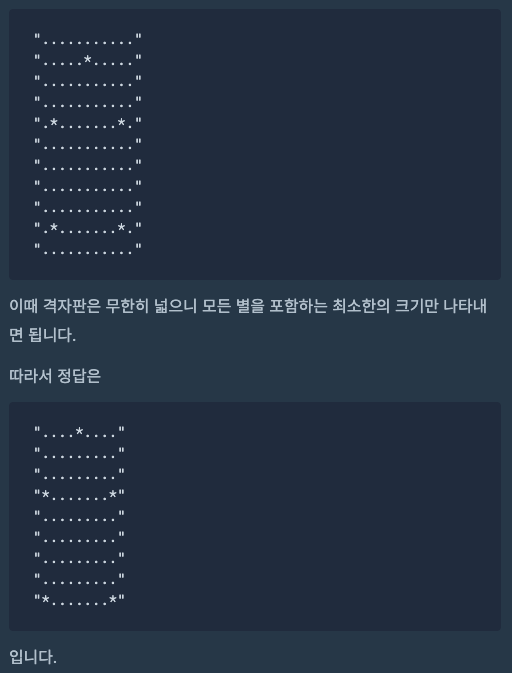

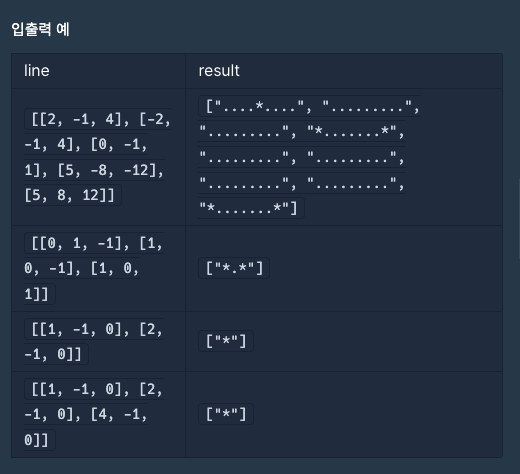
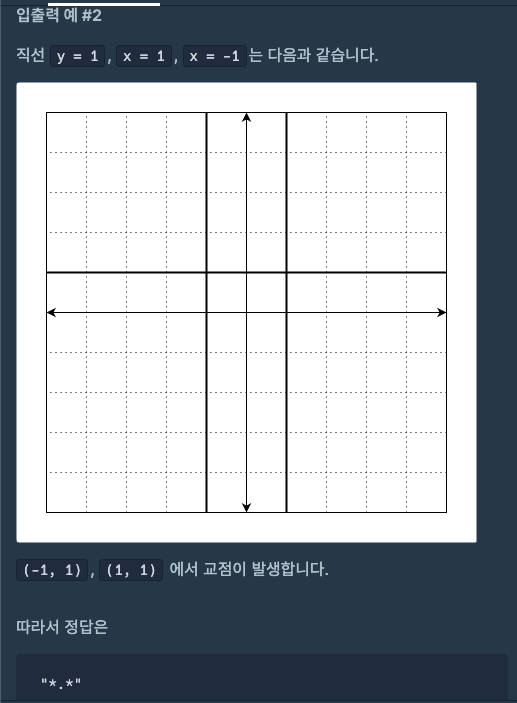
문제 풀이 흐름
- 모든 직선 쌍에 대해 반복
A. 교점 좌표 구하기
B. 정수 좌표만 저장- 저장된 정수들에 대해 x,y 좌표의 최대값, 최소값구하기
- 구한 최대값, 최솟값을 이용하여 2차원 배열의 크기 결정
- 2차원 배열에 별 표시
- 문자열 배열로 변환 후 반환
좌표를 표현해야하니 좌표를 나타내는 클래스를 만든다
class Point{
long x;
long y;
Point(long x, long y){
this.x = x;
this.y = y;
}
}
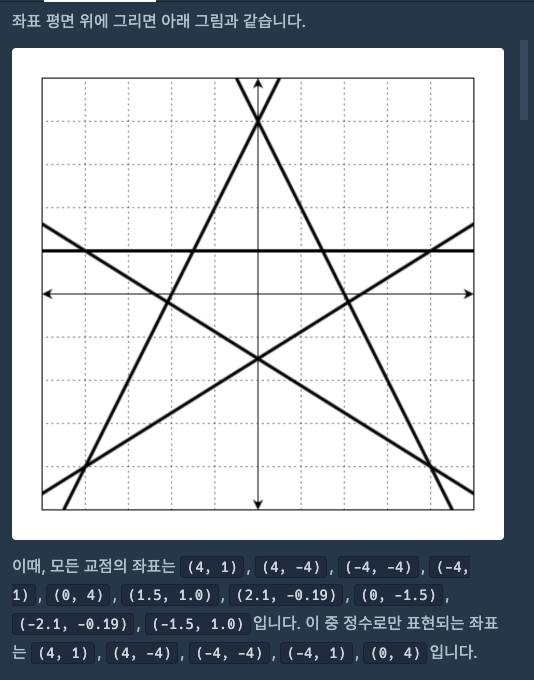
- 무수히 많은 교점이 생기는 직선 쌍은 주어지지 않습니다.
위 제한사항에서 직선 하나는 직선 하나와만 교차한다는 것이 포인트이다
1. 모든 직선 쌍에 대해 반복
- 모든 직선 쌍에대해 반복을 이중 반복문으로 구현한다.
for(int i =0; i < line.length; i++) {
for (int j =i +1; j < line.length; j++){
//line[i], line[j]를 이용하여 1-A, 1-B 수행
}
}1-A. 교점 좌표 구하기
- 두 직선의 교점을 구해야하는데 별도의 메서드로 분리하여 구현한다.
//교점 구해서 반환하기
private Point intersection(long a1, long b1, long c1, long a2, long b2, long c2){
return null;
}
위 식을 이용한 교점을 구하는 방식은 아래에 참고사항으로 나와있다.

private Point intersection(long a1, long b1, long c1, long a2, long b2, long c2){
//교점 구하기
double x = (double) (b1 * c2 - b2 * c1) / (a1 * b2 - a2 * b1);
double y = (double) (a2 * c1 - a1 * c2) / (a1 * b2 - a2 * b1);
// 정수일때만 반환
if(x % 1 != 0 || y % 1 != 0) return null;
return new Point((long) x, (long) y);
}1-B. 정수 좌표만 저장
List<Point> points new ArrayList<>();
for(int i = 0; i < line.length; i++) {
for (int j = i +1; j < line.length; j++) {
Point intersection = intersection(line[i][0],line[i][1],line[i][2],line[j][0],line[j][1],line[j][2])
if(intersection != null) {
points.add(intersection);
}
}
}2. 저장된 정수들에 대해 x,y 좌표의 최댓값, 최솟값 구하기
- 우리의 목표는 별을 표시할 2차원 배열을 정확히 별들만 표시할 수 있을 정도로 작게 잡아야한다.
- 이를 위해 각 좌표의 최댓값과 최솟값을 구해야 한다.
//가장 작은 좌표 찾기
private Point getMinimumPoint(Lint<Point> points) {
//비교할 값을 먼저 만들어둠
long x = Long.MAX_VALUE;
long y = Long.MAX_VALUE;
for(Point p : points){
if(p.x < x) x = p.x;
if(p.y < y) y = p.y;
}
// 가장 작은 좌표를 가진 포인트 반환
return new Point(x,y);
}//가장 큰 좌표 찾기
private Point getMaximumPoint(Lint<Point> points) {
//비교할 값을 먼저 만들어둠
long x = Long.MIN_VALUE;
long y = Long.MIN_VALUE;
for(Point p : points){
if(p.x>x) x = p.x;
if(p.y>y) y = p.y;
}
// 가장 큰 좌표를 가진 포인트 반환
return new Point(x,y);
}3. 구한 최댓값, 최솟값을 이용하여 2차원 배열의 크기 결정
- 배열의 크기를 구해야 하므로 minimum과 maximum을 사용하여 구한 값에 1을 더해야한다
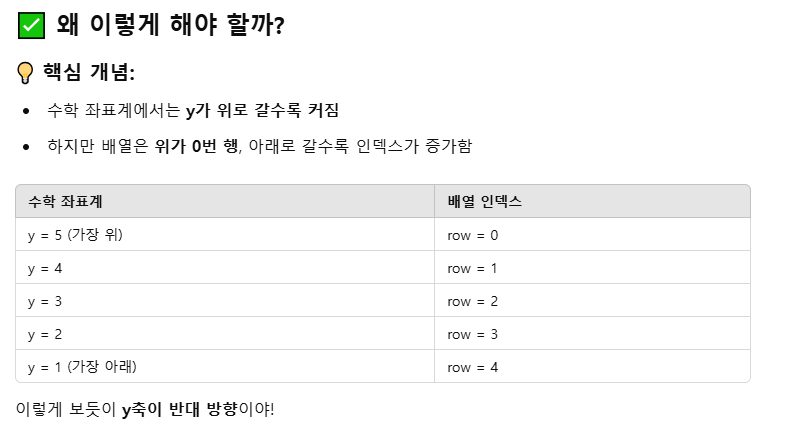
✅ 왜 +1을 하는 걸까?
배열은 0부터 시작하는 인덱스를 사용하기 때문에, 시작점과 끝점을 모두 포함하려면 범위 차이에
+1을 해줘야 함.예:
👉 minimum = (2, 3)
👉 maximum = (5, 8)2~5까지는 4개의 값 (2, 3, 4, 5)
3~8까지는 6개의 값 (3, 4, 5, 6, 7, 8)
Point minimum = getMinimumPoint(points);
Point maximum = getMaximumPoint(points);
int width = (int) (maximum.x - minimum.x + 1);
int height = (int) (maximum.y - minimum.y + 1);
char[][] arr = new char[height][width]; //배열 기준은 행 열
for (char[] row : arr) {
Arrays.fill(row, '.');
}- 최소값과 최대값을 이용하여 width와 height을 구한다.
- width와 height을 이용하여 2차원 배열을 만든다.
- 한 행씩 가져와서 그 행의 내부 배열값을 모두
.으로 채운다. - 문자를 넣어야하므로 자료형은
char로 한다. Arrays.fill(row, '.')는row배열의 모든값을.으로 채운다는 것이다.
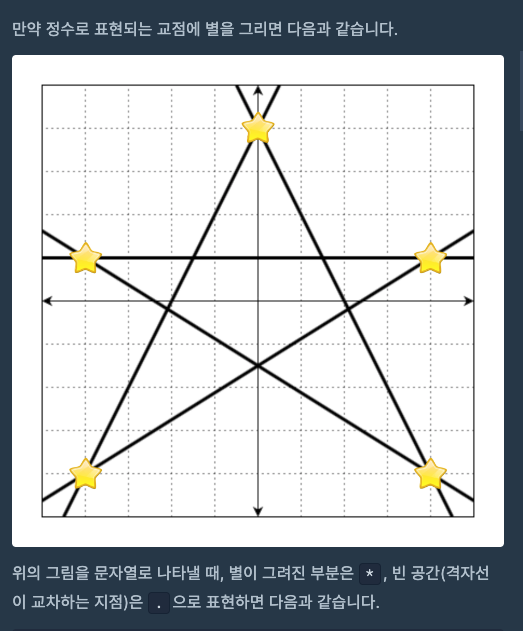
4. 2차원 배열에 별 표시
- 별을 찍는다.
- 별을 찍을 위치는
1-B에서points변수에 저장했으니 이를 순회하며 별을 찍어준다.
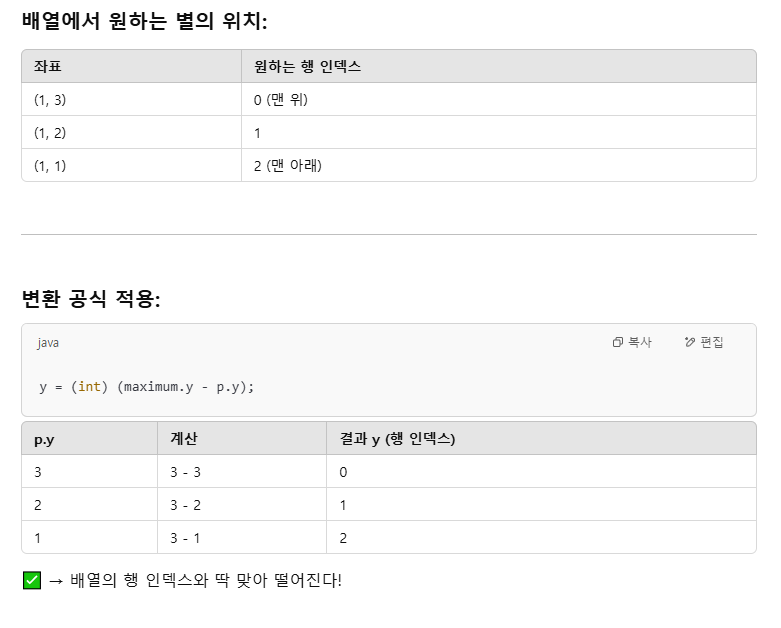
for(Point p : points) {
int x = (int) (p.x - minimum.x);
int y = (int) (maximum.y - p.y);
arr[y][x] = '*'; // 좌표에서는 x,y순이지만 배열에서는 행 열 수준이라 [y][x]로 바꿔줌
}
4-1. 이렇게하는 이유
int x = (int) (p.x - minimum.x);먼저 points 들의 모든 값들은 교점들이고
minimum.x는 그 교점들중 최소값이다.우리는 교점이 있는 최소한의 배열만 만들것이다.
points들 중 최소값은 minimum.x 와 값이 일치할것이고
points 중 p.x - mimun.x를 하면 0 으로 초기화 될것이다.그럼 x값을 배열의 0부터 시작하게 넣을 수있는것이다.
4-2. 이렇게하는 이유
int y = (int) (maximum.y - p.y);
maximum.y는 points중 가장 큰값이고 maximum.y에서 points 에서 가져오는 p.y를 빼줘야 배열의 순서대로 y값이 들어간다.
5. 문자열 배열로 변환 후 반환
//char[][] arr 에서 만든 행 개수 -> arr.length
String[] result = new String[arr.length];
for (int i =0; i < result.length; i++) {
result[i] = new String(arr[i]);
}
return result;-
arr[i]는char[]→ 한 행의 문자 배열 (예:['.', '*', '.']) -
new String(arr[i])은 그 문자 배열을 문자열로 변환 (예:".*.") -
그걸
result[i]에 저장