[알고리즘] 신장트리

Sjin·2021년 1월 21일
알고리즘
0

신장 트리 (spanning tree)

그래프 내의 모든 정점을 포함하는 트리

n개의 정점으로 이루어진 무방향 그래프에서 n-1개의 간선으로 이루어진 트리

  • 하나의 트리에는 다수의 신장트리가 존재할 수 있다.
  • 모든 정점들이 연결되어 있어야 하며, 싸이클을 포함해서는 안된다.

최소 신장 트리 (MST)

무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리

  • 가중치의 합이 최소여야 한다.

  • n개의 정점을 가지는 그래프에 대해 반드시 n-1개의 간선만을 사용해야한다.

  • 사이클이 포함되면 안된다.

  • 그래프에서 최소 비용을 구할때 활용

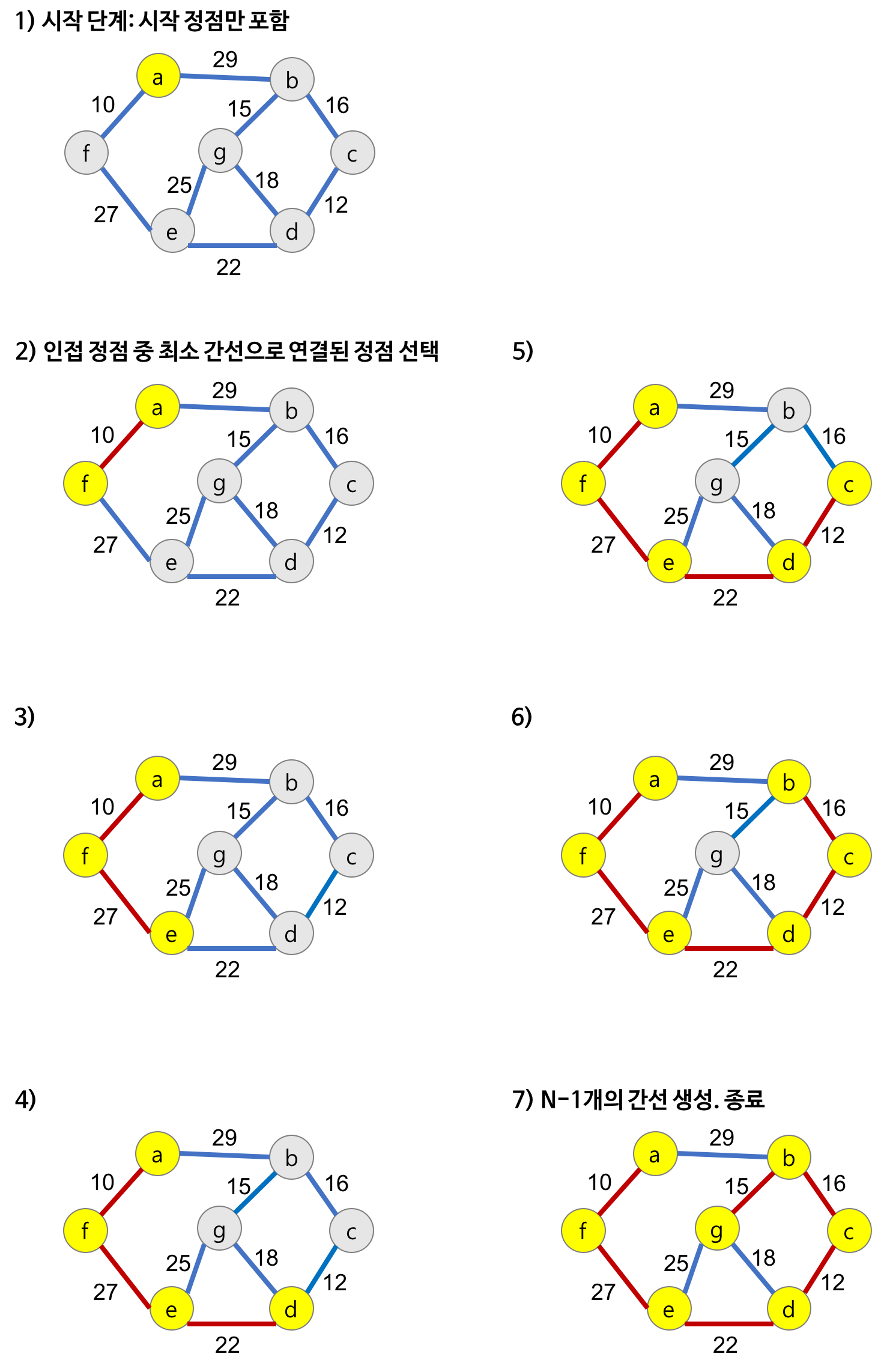
Prim 알고리즘

하나의 정점에서 출발하여 연결된 간선들 중 하나씩 선택하면서 MST를 만들어나가는 방식

  • 정점 선택 기반
  • 이전의 mst에서 확장해 나감

방법

  1. 임의의 정점을 하나 선택
  2. 선택 정점과 인접 정점들 중 최소 비용의 간선으로 연결된 정점을 선택
  3. 연결된 정점에서 다시 2번 수행
  4. 모든 정점이 선택될 때까지 2,3번 과정을 반복

코드

V,E = map(int,input().split())
adj = {i:[] for i in range(V)}
for i in range(E):
  s,e,c = map(int,input().split())
  adj[s].append([e,c])
  adj[e].append([s,c])
  
INF = float('inf')
cnt = 0
key = [INF]*V
mst = [False]*V
p = [-1]*V
p[0] = 0
mst[0] = True
key[0] = 0
u = 0
while cnt < V-1:
  for w,c in adj[u]:
    if not mst[w] and c < key[w]:
      key[w] = c
      p[w] = u
  min = INF
  for i in range(V):
    if key[i] < min:
      min = key[i]
      u = i
  cnt += 1
import heapq

V,E = map(int,input().split())
adj = {i:[] for i in range(V)}
for i in range(E):
  s,e,c = map(int,input().split())
  adj[s].append([e,c])
	adj[e].append([s,c])

# key, mst, 우선순위 큐 준비
INF = float('inf')
key = [INF]*V
mst = [False]*V
pq=[]
#시작 정점 선택 : 0(임의)
key[0] = result = 0
#큐에 시작 정점을 넣음 => (key, 정점인덱스) #우선순위 큐 -> 이진힙 -> heapq 라이브러리 사용
heapq.heappush(pq, (0,0))#우선순위큐 -> 원소의 첫번째 요소 -> key를 우선순위로  #힙의 구조 유지하면서 하나의 원소 넣음
while pq:
  #최솟값 찾기
  k, node = heapq.heappop(pq)
  if mst[node]: continue
  #mst로 선택
  mst[node] = True
  result += k
  #key 갱신 => key 배열/ 큐
  for dest,wt in adj[node]: #(목적지,가중치)
    if not mst[dest] and wt < key[dest]:
      key[dest] = wt
      #큐 갱신 => 새로운 (key,정점) 삽입 => 필요없는 원소는 스킵
      heapq.heappush(pq,(key[dest],dest))

Kruscal 알고리즘

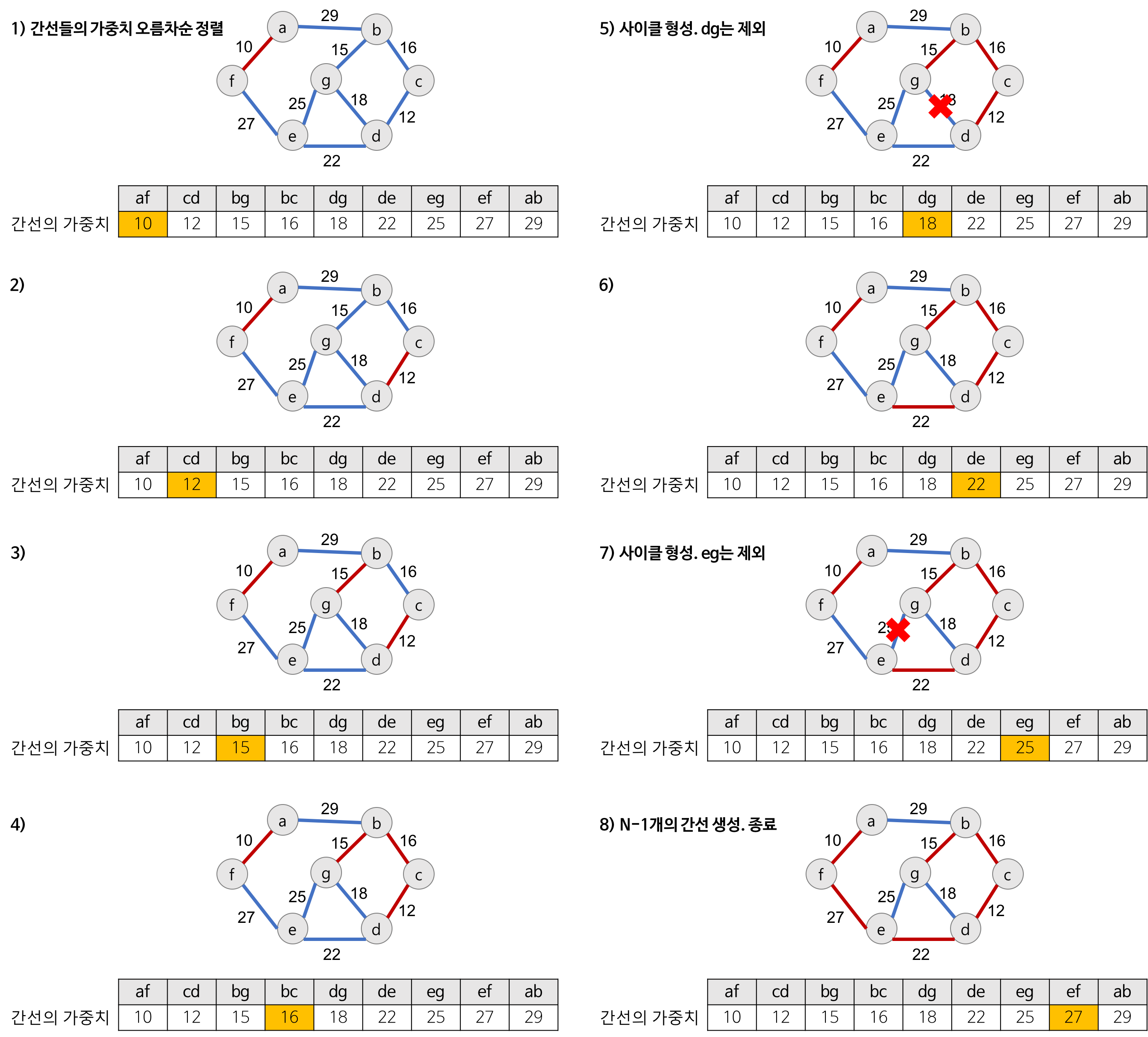
탐욕적인 방법을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것

  • 간선 선택 기반
  • 이전 단계에서 만들어진 신장트리와는 상관없이 무조건 최소 간선만을 선택
  • 각 단계에서 사이클을 형성하지 않는 최소 비용의 간선 선택

방법

  • 간선 정보가 담긴 리스트에서 가중치를 기준으로 오름차순 정렬

  • 가중치가 가장 낮은 간선부터 선택하면서 트리를 확장

    • 선택한 간선으로 인해 사이클이 생긴다면, 그 다음으로 낮은 가중치의 간선을 선택
    • 사이클의 여부는 서로소 집합을 이용해서 정점의 대표자가 같으면 사이클이 발생한 것으로 간주

  • n-1개의 간선이 선택될 때까지 위 과정을 반복

코드

def make_set(x):
  p[x] = x
  
def find_set(x):
  if x == p[x]:
    return x
  else:
    p[x] = find_set(p[x])
    return p[x]
  
def union(x,y):
  px = find_set(x)
  py = find_set(y)
  if rank[px] > rank[py]:
    p[py] = px
  else:
    p[px] = py
    if p[px] == p[py]:
      rank[py] += 1
  #union이 끝나면 흡수된 트리의 종속되어있는 자식들의 대표자도 흡수한 노드로 바꿔줘야하기 때문에 find_set으로 한번 씩 돌림
  for i in range(V):
    find_set(i)
    

V,E = map(int,input().split())
edges = [list(map(int,input().split())) for _ in range(E)]
#간선을 간선 가중치를 기준으로 정렬
edges.sort(key=lambda x:x[2]) #x를 넣으면 x[2]를 반환

#make_set : 모든 정점에 대해 집합 생성
p = [0]*V
rank = [0]*V
for i in range(V):
  make_set(i)

cnt = result = 0
mst = []
#모든 간선에 대해서 반복 -> V-1개의 간선이 선택될 때까지(모든 정점이 연결되려면 간선의 갯수는 V-1개여야하므로)
for i in range(E):
  s,e,c = edges[i][0],edges[i][1],edges[i][2]
  #사이클이면 스킵 : 간선의 두 정점이 서로 같은 집합이면 => find_set
  if finde_set(s) == find_set(e): continue
  #간선 선택
	#=> mst에 간선 정보 더하기 / 두 정점을 합친다 => union
  result += c
  mst.append(edges[i])
  union(s,e)
  cnt += 1
  if cnt == V-1: break #간선을 V-1개 선택했으면 종료

최단경로

간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중 간선의 가중치의 합이 최소 인 경로

  • 하나의 시작 정점에서 끝 정점까지의 최단경로
    • 다익스트라 알고리즘
      • 음의 가중치 허용 x
    • 벨만-포드 알고리즘
      • 음의 가중치 허용
  • 모든 정점들에 대한 최단 경로
    • 플로이드-워샬 알고리즘

다익스트라(Dijkstra) 알고리즘

  • 시작 정점에서 거리가 최소인 정점 선택해 나감
  • 탐욕 기법을 사용
  • MST의 프림 알고리즘과 유사

코드

#다익스트라 + 인접리스트
V,E = map(int,input().split())
adj = {i:[] for i in range(V)}
for i in range(E):
  s,e,c = map(int, input().split())
  adj[s].append([e,c])
INF=float('inf')
#dist, selected 배열 준비
dist = [INF]*V
selected = [False]*V

dist[0] = 0 #시작점 선택 
cnt = 0
while cnt < V: #모든 정점이 선택될때까지 
  #dist가 최소인 정점 찾기
  min = INF
  for i in range(V):
    if not selected[i] and dist[i]<min:
      min = dist[i]
      u = i #아직 선택되지 않고 dist의 값이 최소인 정점: u
  #정점 u의 최단거리 결정
  selected[u] = True
  cnt += 1
  #정점 u에 인접한 정점에 대해서 간선완화
  for w,cost in adj[u]: #도착 정점, 가중치
  	if dist[u]+cost < dist[w]:
      dist[w] = dist[u]+cost
print(dist)

플로이드 워샬 알고리즘

개념

다익스트라 알고리즘은 특정 두 노드 사이의 최단 경로만 알 수 있다. 하지만 플로이드 워샬 알고리즘은 모든 정점들에 대한 최단 경로를 알 수 있기 때문에 알아두면 편리한 알고리즘이다. 이 알고리즘은 모든 점을 각각 중간 지점을 정했을 때, 중간 지점 ~ 시작 지점까지의 최단 경로, 중간 지점 ~ 도착 지점까지의 최단 경로를 더해서 시작 지점부터 도착 지점까지의 최단 경로를 구하는 방식이다.

시간 복잡도

O(n^3)

구현 과정

  • 각 정점들간의 최단 경로를 담아두기 위한 2차원 리스트를 준비한다.

    행과 열 번호가 같은 자기 자신은 거리가 0이므로 0으로 초기화 하고, 나머지 경로는 inf로 초기화한다.

  • 중간 지점을 설정하기 위해 1부터 n까지 for문을 순회한다.

    • 중간 지점을 m이라 두고, 내부에서 2중 for문(i: 시작 지점, j: 도착 지점)을 순회한다.

      시작~중간 + 중간~도착이 최소가 되면 최솟값으로 갱신

  • 3중 for문을 돌고나면 모든 정점에 대한 최단 경로를 알 수 있다.

코드

INF = float('inf')
dist = [[INF]*(n+1) for _ in range(n+1)]
for i in range(1,n+1):
  dist[i][i] = 0
  for u,w,c in fares:
    dist[u][w] = c
    dist[w][u] = c

for m in range(1,n+1):
  for i in range(1,n+1):
    for j in range(1,n+1):
      val = dist[i][m] + dist[m][j]
      if val < dist[i][j]:
        dist[i][j] = val

참고

https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html

profile
Sjin
프론트엔드 개발에 관심있는 주니어 웹 개발자입니다.
이전 포스트

[OS] 교착 상태(DeadLock)

다음 포스트

[JavaScript] 스코프

0개의 댓글