[Java] 프로그래머스 - 카펫

프로그래머스 - 카펫

풀이 1

import java.util.ArrayList;
import java.util.List;

class Solution {
	public int[] solution(int brown, int yellow) {
		// 1. 노란색의 개수로 가능한 약수의 조합을 구함
		// 2. 모든 약수 조합으로 사각형을 만들고, 문제의 조건(가로 >= 세로) 만족하면서 가장 괄호의 길이 긴것?

		// 가능한 약수의 쌍(가로 X 세로 형태)
		List<int[]> pairs = new ArrayList<>();
		// 에라토스테네스의 체 : 제곱근까지만 확인하면 약수 구하기 가능 
		for (int i = 1; i <= (int)Math.pow(yellow, 0.5); i++) {
			if (yellow % i == 0) {
				// 몫
				int mock = yellow / i;

				// 가로가 더 긴값으로 갱신
				int x = Math.max(i, mock);
				int y = Math.min(i, mock);
				int[] pair = new int[] {x, y};
				pairs.add(pair);
			}
		}

		int[] result = new int[2];

		for (int[] pair : pairs) {
			int x = pair[0];
			int y = pair[1];

			// 가로 길이가 더 긴것으로 갱신
			if (x > result[0]) {
				// 브라운 개수의 합이 만든 사각형과 같으면 갱신
				if ((x + 2) * (y + 2) == yellow + brown) {
					result[0] = x + 2;
					result[1] = y + 2;
				}
			}
		}

		return result;
	}
}

• 다른 블로그 풀이를 봐도 왜 -2를 하고 곱하는 등 왜 이렇게 나오지? 이런거가 잘 이해가 안가시면 아래 내용 보시면 좋을 것 같습니다!

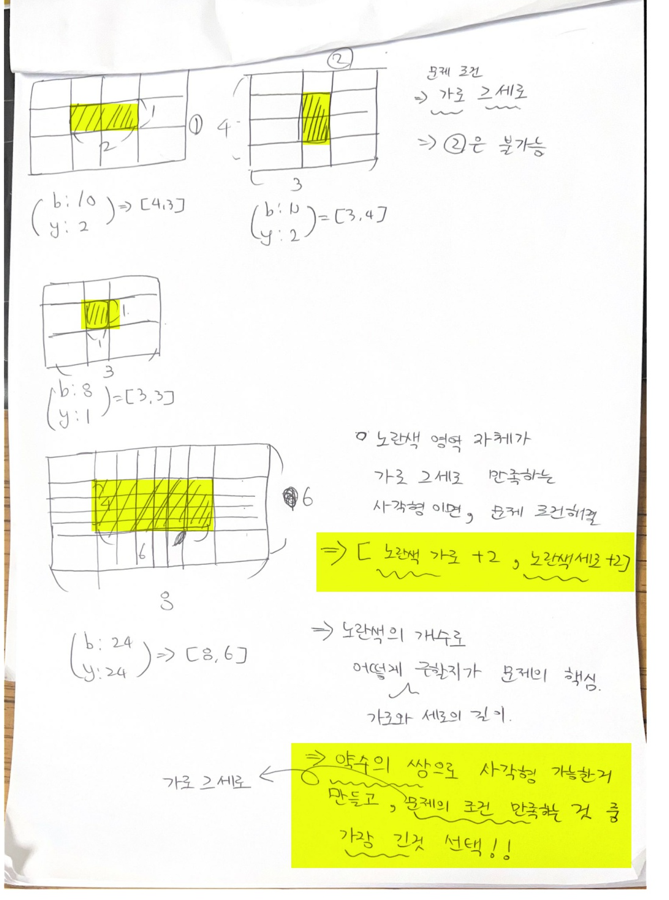
• 각각의 테스트 케이스 그림으로 나타내면 위와 같습니다.

• 첫번째 노란색이 2개라면, 가로로 가운데에 있을 수 있고, 세로로 가운데에 있을 수 있습니다.

  • 하지만 문제의 조건에 부합 하지 않습니다(가로 >= 세로)

• 두번째 예제는 노란색이 1개라면 한가지 경우 뿐이 없습니다.

• 위 2개의 케이스에서 전체 가로의 길이는 노란색 가로 +2, 노란색 세로 +2 임을 알 수 있습니다.(노란색 부분이 전체 사각형에서 가운데에 위치하니깐 적어도 위아래 +1씩)

• 세번째 예제는 노랜색이 24개이니, 가운데에 넣어주고, 위아래 1씩 더해준 값입니다.

• 따라서 약수의 쌍으로 노란색 사각형을 만들고 문제의 조건을 만족하는 쌍 중 가로가 제일 긴 것의 +2씩을 해주면 정답입니다!

• 하지만 이렇게 하면 놓치는 점이 있습니다. 브라운 사각형 부분을 고려를 안했습니다.

• 예제를 보다보니 브라운 + 노란색의 합이 전체 사각형의 넓이와 같은 점을 발견했습니다.

• 따라서 브라운 + 노란색 합과 새로 만든 카펫의 넓이를 비교 해주는 것 까지 진행하면 정답입니다!

• 약수 찾을때는, 에라토스테네스의 체(제곱근 까지만 나눠보면 약수 구함)를 이용하였습니다.

  • ex) 8 -> 2 x 4 or 4 x 2는 같으니깐 제급근 까지만 확인하면 가능
  • 가로가 더 길어야 하니깐 큰값을 앞으로 배정했습니다.

풀이2 - 메서드화

import java.util.*;

class Solution {
    public int[] solution(int brown, int yellow) {
        
        if(yellow == 1) {
            return new int[] {3, 3};
        }
        if(yellow == 2) {
            return new int[] {4, 3};
        }
        // 1. yellow가 더 길어야 하니 가능한 조합 모두 구하기
        List<int[]> comb = getCombinationArr(yellow);
        // 2. brown 갯수와 동일한 조합 찾기
        int[] result = getCapetSize(comb, brown);
        // 3. 결과 반환
        return result;
        
    }
    
    public List<int[]> getCombinationArr(int number) {
        List<int[]> combList = new ArrayList<>();
        // 1. 가능한 모든 조합 찾기(에라토스테네스의체)
        for(int i = 1; i <= (int)Math.sqrt(number); i++) {
            // 나눠 떨어진다는 것은 가능한 조합
            if(number % i == 0) {
                int temp = number / i;
                // 둘 중 큰 수를 앞으로 오는 배열을 정답 리스트에 넣기
                if(temp >= i) {
                    combList.add(new int[] {temp, i});
                }
                else {
                    combList.add(new int[] {i, temp});
                }
            }
        }
        // 2. 결과 반환
        return combList;
    }
    
    public int[] getCapetSize(List<int[]> capetYellowSizeCandidates, int brownCount) {
        int[] result = new int[2];
        for(int[] candidate : capetYellowSizeCandidates){
            // 긴것이 앞에니까 문제 조건 : 가로 >= 세로, 가로가 긴것
            int yellowWidth = candidate[0];
            int yellowHeight = candidate[1];
            // 카펫 가운데 노랑색 -> 테두리 1칸씩 브라운 -> (가로 + 2) * (세로 + 2)가 전체 넓이
            int capetArea = (yellowWidth + 2) * (yellowHeight + 2);
            
            // 전체 넓이 : 노란색 개수 + 갈색 갯수(1칸의 넓이는 1이니깐)
            // 노란색 개수(노란색 넓이) -> 더한것이 전체 넓이와 같다면 정답
            if(capetArea == yellowWidth * yellowHeight + brownCount) {
                // 맞는 yellow 갯수를 찾았으니 전체 사각형 가로 세로 길이로 갱신
                result[0] = yellowWidth + 2;
                result[1] = yellowHeight + 2;
                break;
            }
        }
        
        return result;
        
    }
}

• 상세 풀이는 위 방법과 같습니다.