문제
접근 방법
사용한 수의 개수에 따라 저장하는 건 불가피하다고 생각했다.
사용한 수의 개수는 어떻게 알 수 있을까?
정수 4의 m이 2일 경우를 생각해보자.
2+2, 1+3, 3+1이 있다. 모두 1, 2, 3으로 조합됐다. 2에 뒤에는 2가 붙었다. 2는 어디서 왔을까? n이 2고 m이 2인 경우에서 가져왔을 것이다. 1+3, 3+1도 마찬가지로 n이 1, 3이고 m은 3, 1일 것이다.
간단하게 말하자면 3, 2, 1 만큼 떨어진 곳에서 가져오는데 사용한 개수가 1개 차이 나는 것을 확인하는 것이다. (1, 2, 3이 1개만큼만 더 붙으면 돼서 그렇다)
코드
#include <iostream>
using namespace std;
long long dp[1001][1001]; // n m
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
dp[1][1] = 1; // 1
dp[2][1] = 1; // 2
dp[2][2] = 1; // 1+1
dp[3][1] = 1; // 3
dp[3][2] = 2; // 1+2 2+1
dp[3][3] = 1; // 1+1+1
int T, min = 4;
cin >> T;
while (T--)
{
int n, m;
cin >> n >> m;
for (int i = min; i <= n; ++i)
{
for (int j = (i - 1) / 3; j <= i; j++)
{
dp[i][j] = (dp[i - 1][j - 1] + dp[i - 2][j - 1] + dp[i - 3][j - 1]) % 1000000009;
}
}
cout << dp[n][m] << "\n";
if (n > min)
min = n;
}
return 0;
}풀이
모든 경우를 확인할 필요가 없다. 그것을 간접적으로 알려주는 예제가 예제 2이다.
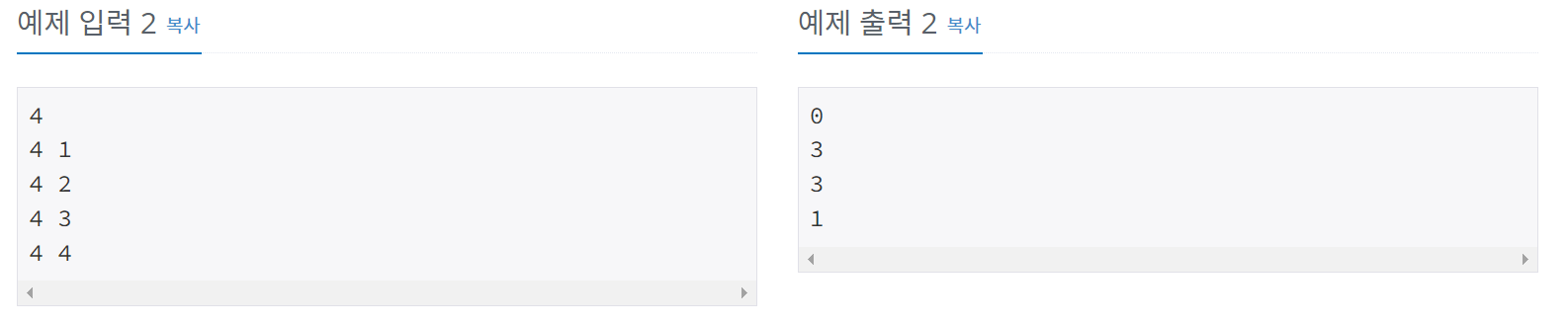
4를 1개의 경우로 해결할 순 없다. (1개 쓸 수 있는 경우는 최대 3이므로)
4를 5개로 해결할 순 없다. (사용할 수 있는 수는 최소가 1인데 그렇다면 4까지만 가능하므로)
이것은 4에만 국한된 것이 아니다.
최댓값인 3을 최소한으로 이어 붙였을 때 (3+3+....+3+3)보다 작은 값은 확인할 필요가 없다. 최솟값인 1을 최대한으로 이어 붙였을 때 (1+1+....+1+1)보다 높은 값은 무시하면 된다.
그러한 점을 생각하여 반복문을 구성해주면 마치 계단처럼 훑으면서 값을 갱신할 것이다.
