[C++][백준 1660] 캡틴 이다솜

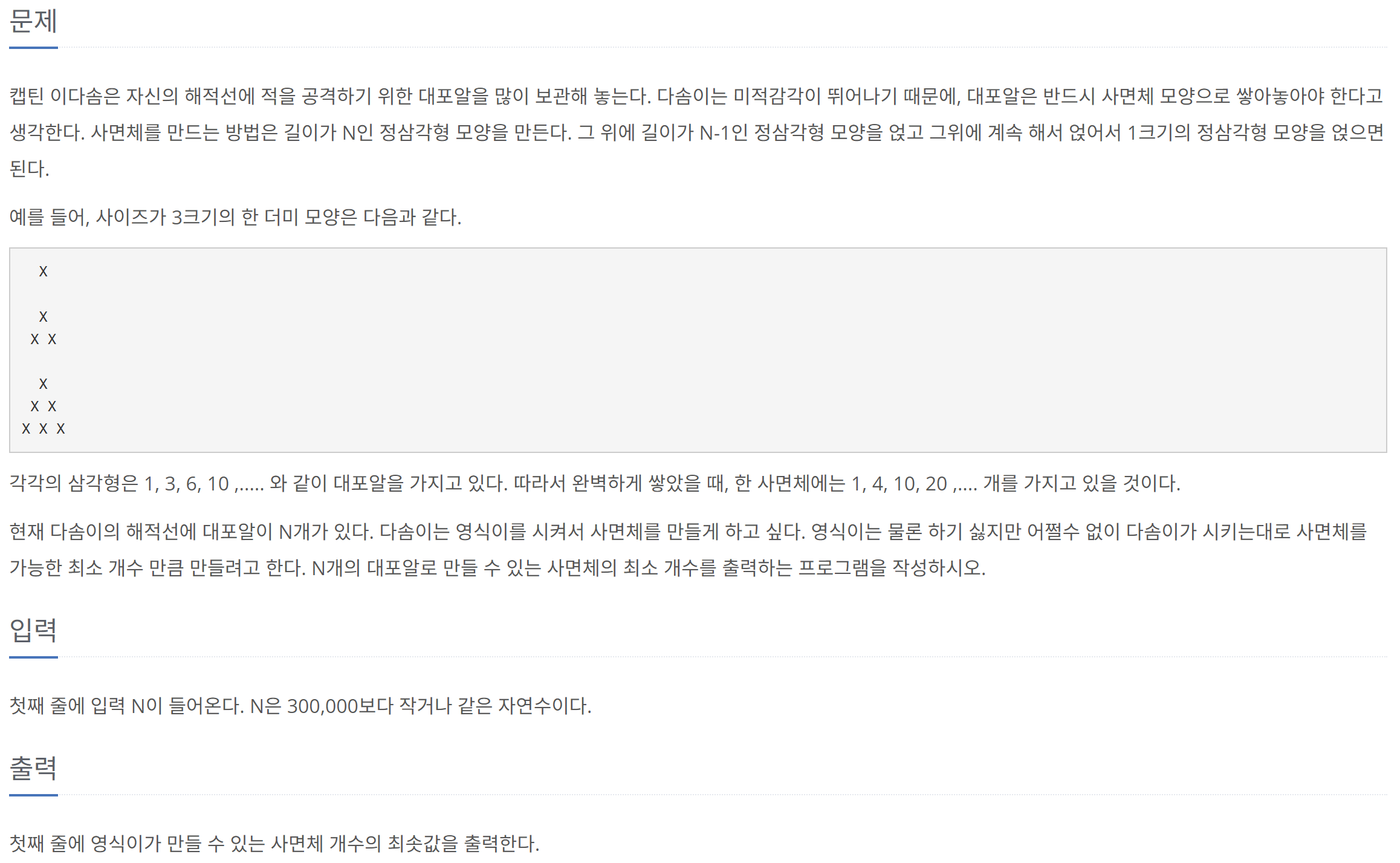
문제

접근 방법

삼각형 대포알 개수 = 1부터 x까지의 합
사면체 대포알 개수 = 1부터 x까지의 삼각형 대포알 개수

사면체 대포알 개수는 공식 또는 누적합을 활용하여 구할 수 있다.

코드

#include <iostream>
#include <vector>
using namespace std;
#define MAX_NUMS 121
int nums[MAX_NUMS], N;
vector<int> dp;
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);

    for (int i = 1; i < MAX_NUMS; ++i)
    {
        nums[i] = i * (i + 1) * (i + 2) / 6;
    }

    cin >> N;
    dp = vector<int>(N + 1);

    for (int i = 1; i < N + 1; ++i)
    {
        dp[i] = i;
    }

    for (int i = 0; i < MAX_NUMS; ++i)
    {
        for (int j = nums[i]; j <= N; ++j)
        {
            dp[j] = min(dp[j], dp[j - nums[i]] + 1);
        }
    }

    cout << dp[N];
    return 0;
}

풀이

사면체 대포알의 개수를 구한 뒤 반복문을 돌며 사면체 대포알로 대체할 수 있는지 확인하면 된다.

사면체 대포알로 대체할 수 있다면 개수는 사면체 개수-1만큼 줄일 수 있기에 사면체 개수의 최솟값을 구할 수 있다.