[C++][백준 16970] 정수 좌표의 개수

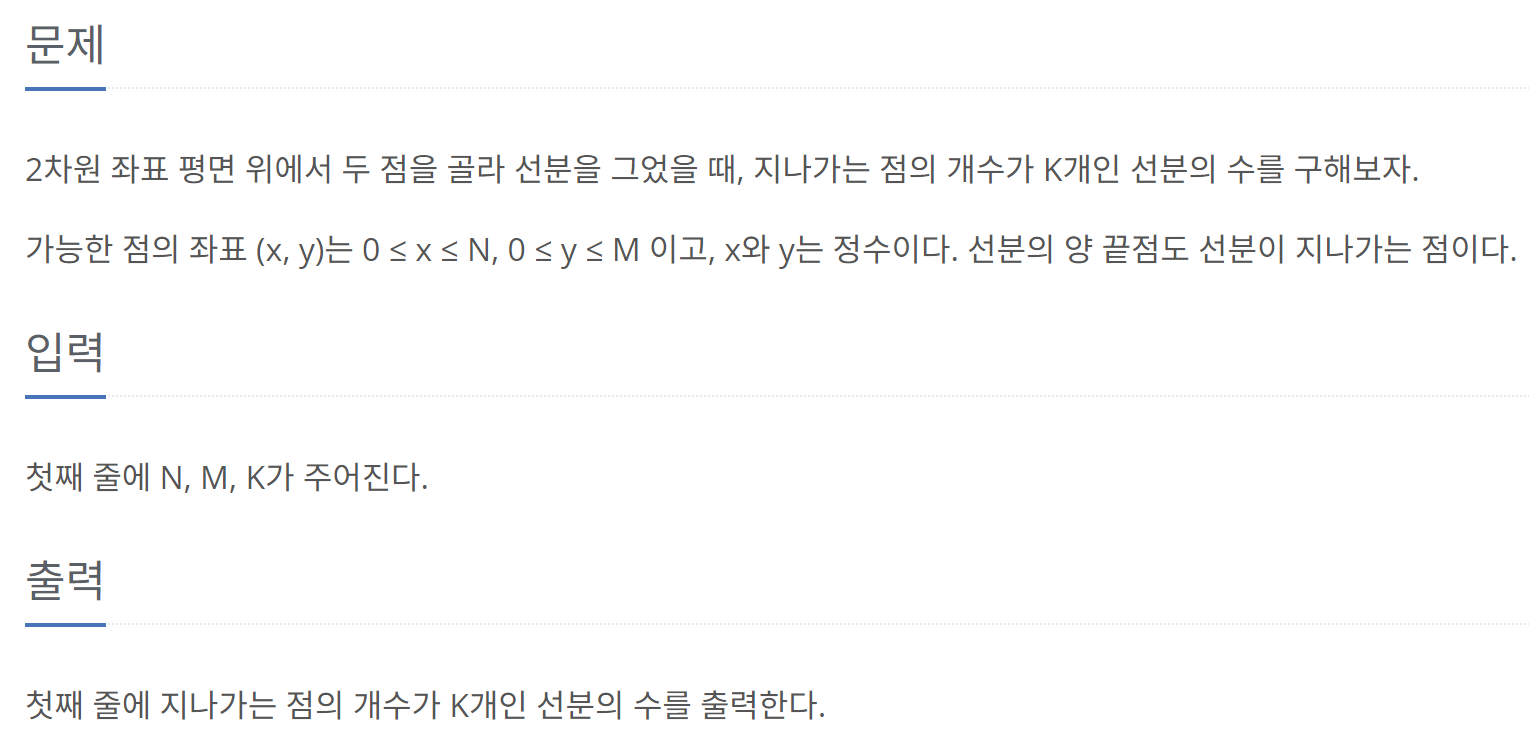
문제

접근 방법

N과 M이 최대 50이기에 모든 경우를 확인해 주어도 문제없다.

코드

#include <iostream>
using namespace std;
int N, M, K, answer;

int gcd(int a, int b)
{
    if (!b)
    {
        return a;
    }

    return gcd(b, a % b);
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0);

    cin >> N >> M >> K;

    for (int i = 0; i <= N; ++i)
    {
        for (int j = 0; j <= M; ++j)
        {
            for (int k = 0; k <= N; ++k)
            {
                for (int l = 0; l <= M; ++l)
                {
                    if (abs(gcd(k - i, l - j)) + 1 == K)
                    {
                        ++answer;
                    }
                }
            }
        }
    }

    cout << answer / 2;
    return 0;
}

풀이

가로와 세로 길이의 최대공약수를 구하여서 1을 더해주면 된다.
최대공약수의 값은 길이가 정수가 되는 일정 단위로 잘랐을 때의 개수인 것이다.
만약 길이가 6, 3일 경우 최대 공약수는 3이다. 길이를 2, 1 단위를 잡고 배치할 시 3번 배치할 수 있다. 정수 위치에 배치할 수 있다는 건 점이 존재한다는 것이다.
1을 더하는 이유는 시작점이기 때문이다.