[C++][백준 23048] 자연수 색칠하기

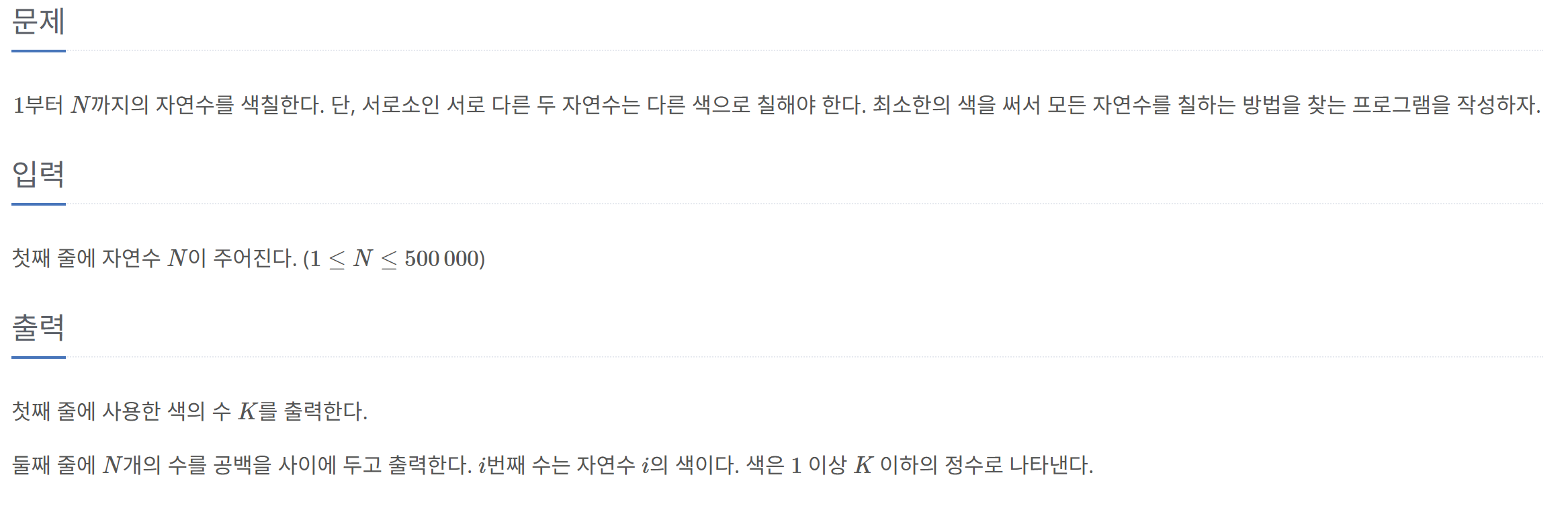
문제

접근 방법

특정 수의 배수는 동일한 색으로 칠할 수 있습니다.
이미 칠한 경우에는 무시하고 넘어가면 됩니다.

즉 2를 예시로 들면 2의 배수인 4, 6, 8, ..., 2X는 모두 2와 같은 색을 칠할 수 있습니다.
이후 3의 경우에는 3의 배수인 6, 12는 이미 칠해졌기에 9, 15와 같은 수를 같은 색으로 칠할 수 있습니다.

코드

#include <iostream>
#include <vector>
using namespace std;
int N, cnt;
vector<int> v;
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> N;
    v = vector<int>(N + 1);

    v[1] = ++cnt;
    for (int i = 2; i <= N; ++i)
    {
        if (v[i])
        {
            continue;
        }

        v[i] = ++cnt;

        for (int j = i + i; j <= N; j += i)
        {
            v[j] = cnt;
        }
    }

    cout << cnt << "\n";
    for (int i = 1; i <= N; ++i)
    {
        cout << v[i] << " ";
    }
    return 0;
}

풀이

규칙을 살펴보면 에라토스테네스의 체를 사용해야 함을 알 수 있습니다.
2부터 N까지 수 중에 특정수가 소수인 경우 새로운 색으로 칠한 뒤 소수의 배수를 같은 색으로 칠해주면 됩니다.

소수가 아닌 경우 이미 이전 소수의 배수에 포함되어 칠해졌을 것이기 때문입니다.