걷기 1459

문제

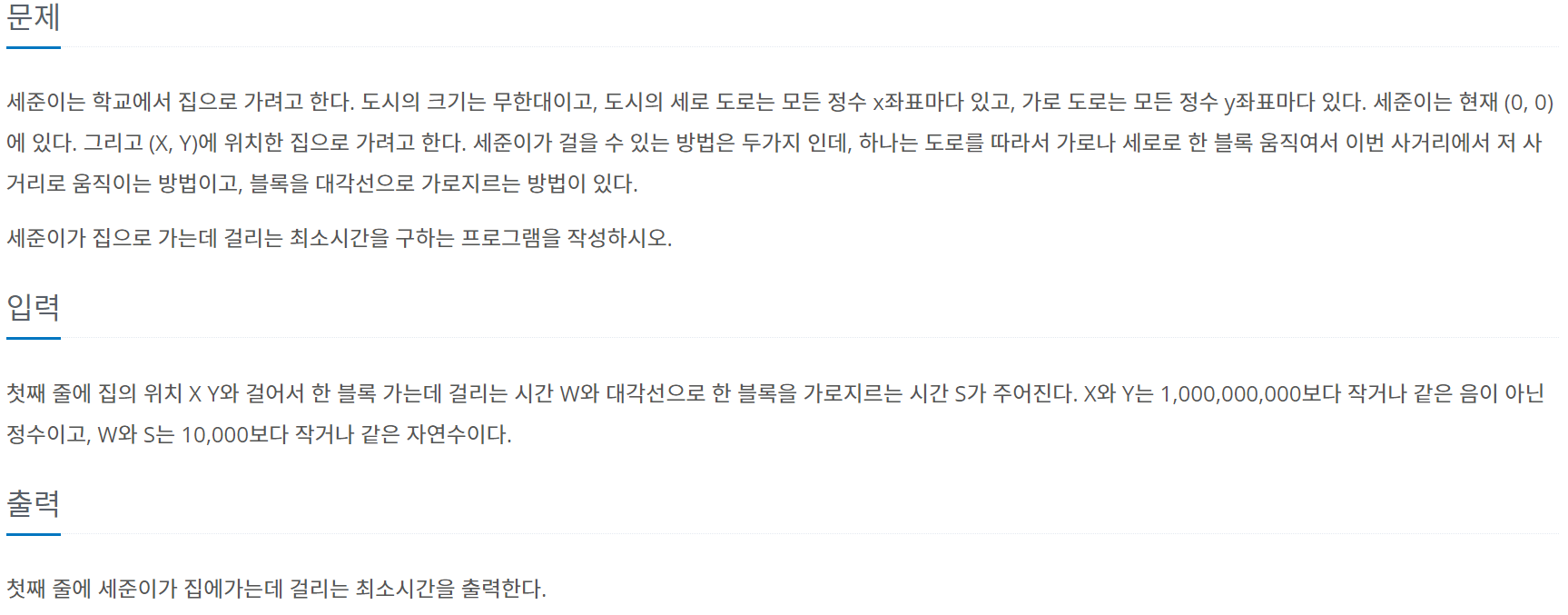
접근 방법

예제를 통해 3가지 경우를 알 수 있다.
대각보다 직선으로 가는 것이 더 빠른 경우,
직선 (격차), 대각 (작은 값) 혼합하는 경우
대각으로 가는 경우 (1칸 차이는 직선으로)

코드

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    unsigned long long X, Y, W, S, ret;
    cin >> X >> Y >> W >> S;
    if ((W << 1) < S)
    {
        ret = (X + Y) * W;
    }
    else
    {
        if (X > Y)
        {
            swap(X, Y);
        }
        ret = X * S + (Y - X) * W;
        unsigned long long i = ((X + Y) % 2 == 1 ? 1 : 0);
        ret = min((Y - i) * S + W * i, ret);
        // ret=X*S+
    }
    cout << ret;
    return 0;
}

풀이

두 값의 합이 짝수인지 홀수인지 확인해야 하는 데 잘못하고 하나의 값만 짝수인지 확인해서 풀려 했다. (대각선으로 가면 항상 (1, 1) (2, 2) (3, 1)같이 두 수의 합이 짝수이므로 두 값의 합이 짝수이다)
피곤한 상태에서는 제대로 된 생각을 못 하는 것 같기도 하다.