[C++][백준 11403] 경로 찾기

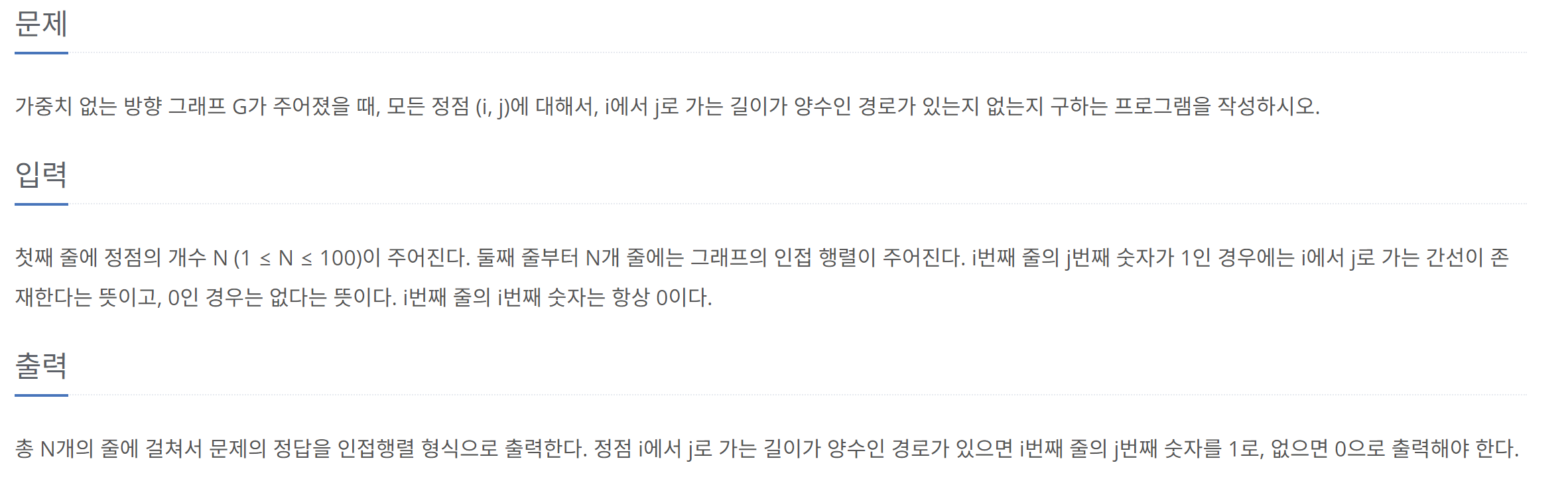
문제

접근 방법

A에서 C로 간다고 할 때 A에서 B로 갈 수 있고 B에서 C로 갈 수 있다면 A에서 C로 갈 수 있다고 할 것이다.

그러한 점을 생각하여서 풀면 된다.

코드

#include <iostream>
#include <vector>
using namespace std;
vector<vector<bool>> graph;
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int N;
    cin >> N;
    graph = vector<vector<bool>>(N, vector<bool>(N));
    for (int i = 0; i < N; ++i)
        for (int j = 0, k; j < N; ++j)
            cin >> k, graph[i][j] = k;
    for (int i = 0; i < N; ++i)
        for (int j = 0; j < N; ++j)
            for (int k = 0; k < N; ++k)
                if (graph[j][i] && graph[i][k])
                    graph[j][k] = true;
    for (int i = 0; i < N; ++i)
    {
        for (int j = 0, k; j < N; ++j)
            cout << graph[i][j] << " ";
        cout << "\n";
    }
    return 0;
}

풀이

플로이드 워셜을 사용하면 된다.
N이 최대 100이기에 N^3이어도 괜찮다.