비숍 1799

문제

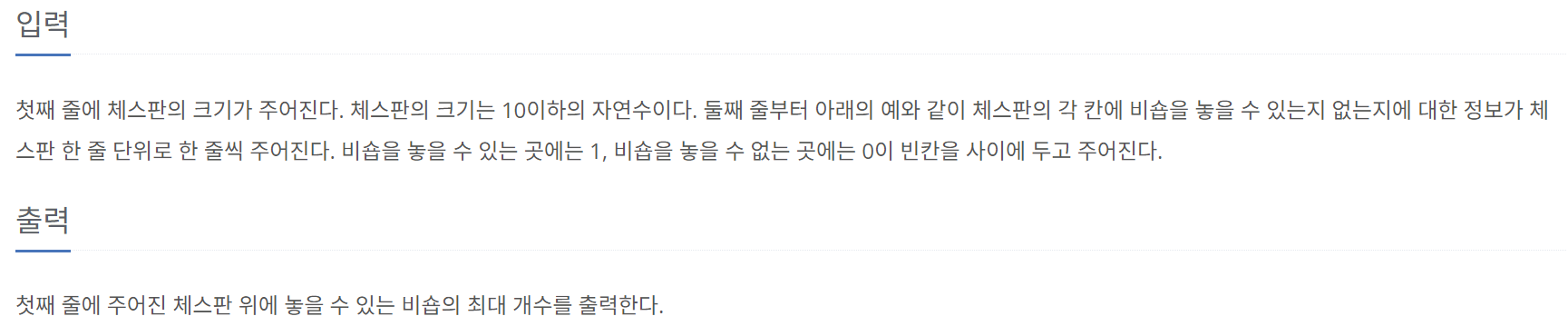
접근 방법

N-Queen하고 비슷한 유형이다.
N-Queen은 상하좌우 대각선을 안 겹친다면 비숍은 대각선만 안 겹친다.
오히려 대각선을 안 겹치게 하기에 퀸 문제보다 더 많은 경우를 볼 수 있다. (퀸은 가로, 세로도 제외하기에 더 적은 경우다)

일정한 대각선의 존재하는 값들은 일차방정식 때문에 특정한 성질을 가지고 있다.
y=x+c에 해당하는 값들은 서로 비례하여 증가하기에 y-x=c이다. y가 더 작을 경우도 존재하기에 n을 더해주면 0 밑으로 내려가지 않는다.
y=-x+c에 해당하는 값은 서로 반비례하기에 y+x=c이다.

결국 두 수의 조합은 2*n을 넘지 못한다. (n 밑의 값이다)

y+x, y-x+n이 방향에 맡게 겹친다면 해당 좌표는 사용할 수 없는 것이다.

코드

#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> pii;
vector<vector<int>> map;
vector<vector<bool>> isCross;
vector<vector<pii>> bishop;
int n;
void dfs(int len, int depth, vector<pii> &v, int &ret)
{
    ret = max(depth, ret);
    if (len == v.size())
        return;
    dfs(len + 1, depth, v, ret);

    int y = v[len].first, x = v[len].second;

    if (!map[y][x])
        return;

    int leftCross = x + y;
    if (isCross[0][leftCross])
        return;
    int rightCross = y - x + n;
    if (isCross[1][rightCross])
        return;
    isCross[0][leftCross] = isCross[1][rightCross] = true;
    dfs(len + 1, depth + 1, v, ret);
    isCross[0][leftCross] = isCross[1][rightCross] = false;
}
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> n;
    bishop = vector<vector<pii>>(2, vector<pii>());
    map = vector<vector<int>>(n, vector<int>(n));
    isCross = vector<vector<bool>>(2, vector<bool>(2 * n));
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; ++j)
        {
            cin >> map[i][j];
            if ((i + j) % 2)
                bishop[1].push_back({i, j});
            else
                bishop[0].push_back({i, j});
        }
    int ret1 = 0, ret2 = 0;
    dfs(0, 0, bishop[0], ret1);
    dfs(0, 0, bishop[1], ret2);
    cout << ret1 + ret2;
    return 0;
}

풀이

대각선 말고도 흑백을 구분하여 풀어야 한다.
흑과 백은 서로 겹칠 일이 없기에 모든 블록을 탐색하기보단 흑색에 해당하는 값만, 백은 백색에 해당하는 값만 확인하면 되는 것이다.

전체 경우의 수를 제곱하는 것보단 반으로 나눈 경우의 수를 제곱한 것을 두 번 하는 것이 더 적기에 흑백을 나누는 것이다.