순위 49191

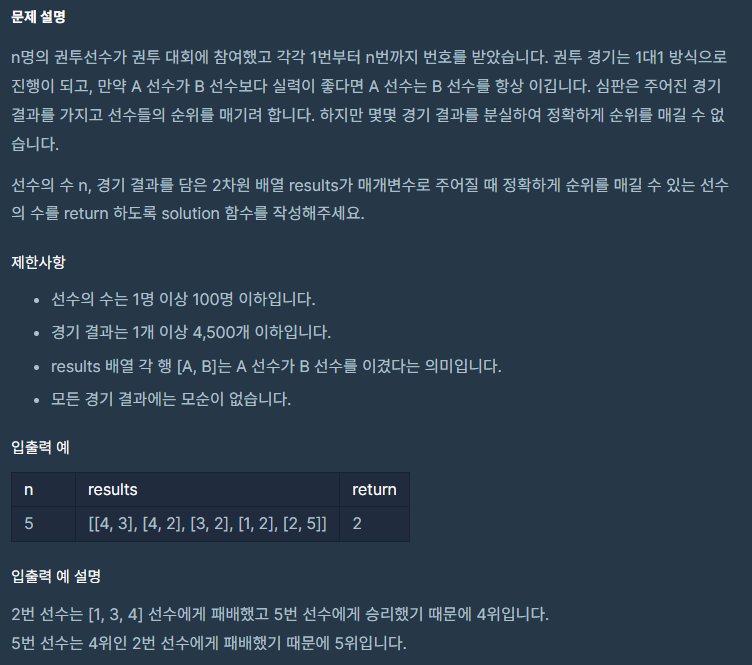
문제

첫 번째 접근 방법

이긴다는 것은 1번도 지지 않았다는 것이고 꼴등이라는 것은 나를 제외한 모든 이들에게 졌다는 것이다.
예제를 보자.
4->3
4, 3, 1->2->5
목적지에 있는 값들에 1씩 올린다고 생각해보자.
1->2->5 (2, 5)
2->5 (5)
3->2->5 (2, 5)
4->2->5 (2, 5)
4->3->이미 갔다 (3)
5-> 0

첫 번째 실패

정렬해주고 뒤에서부터 순서대로 n-1, n-2, n-3...가 되는지 확인해줬다. 하지만 문제가 있었다. 중간에서 결정 나는 경우도 있는 것이다. 나를 제외한 k만큼의 인원에게 이기고 n-k-1만큼의 인원에게 진다면 나의 순위는 결정된다.

두 번째 접근 방법

아마도 이기는 경우도 생각해봐야 했던 것 같다. 이기는 경우를 더해주고 지는 경우를 더해준다면 n-1만큼의 합이 나올 것이다. 즉 모두와 시합을 해보지는 않아도 상대방의 전적을 통해 나의 승리로 간주하거나 나의 패배로 간주해서 n-1만큼의 전적이 나오는지 확인하는 것이다.

코드

#include <string>
#include <vector>
#include <queue>
using namespace std;
int solution(int n, vector<vector<int>> results)
{
    int answer = 0;
    vector<vector<int>> lMap(n + 1), wMap(n + 1);
    vector<bool> isVisted(n + 1);
    vector<int> cnt(n + 1);
    queue<int> q;
    for (auto r : results)
    {
        lMap[r[0]].push_back(r[1]);
        wMap[r[1]].push_back(r[0]);
    }
    for (int i = 1; i <= n; ++i)
    {
        fill(isVisted.begin(), isVisted.end(), false);
        q.push(i);
        while (!q.empty())
        {
            int cur = q.front();
            q.pop();
            for (int next : lMap[cur])
            {
                if (isVisted[next])
                    continue;
                isVisted[next] = true;
                ++cnt[next];
                q.push(next);
            }
        }
    }
    for (int i = 1; i <= n; ++i)
    {
        fill(isVisted.begin(), isVisted.end(), false);
        q.push(i);
        while (!q.empty())
        {
            int cur = q.front();
            q.pop();
            for (int next : wMap[cur])
            {
                if (isVisted[next])
                    continue;
                isVisted[next] = true;
                ++cnt[next];
                q.push(next);
            }
        }
    }
    for (int i = 1; i <= n; ++i)
    {
        if (cnt[i] == n - 1)
            ++answer;
    }
    return answer;
}

풀이

다른 사람의 전적이 나의 전적이기도 한 것을 고려하면 풀리는 문제이다.
이기는 경우의 단방향 그래프와 지는 경우의 단방향 그래프를 만들어 탐색하는 방법을 사용했다.
중복되는 코드가 많고 더러운 것 같기도 하다.
다른 사람의 풀이를 보니 이차원 배열과 삼중 For문을 사용하여 이기는 경우를 연결했던데 깔끔하고 좋은 것 같다.