아기 상어 2 17086

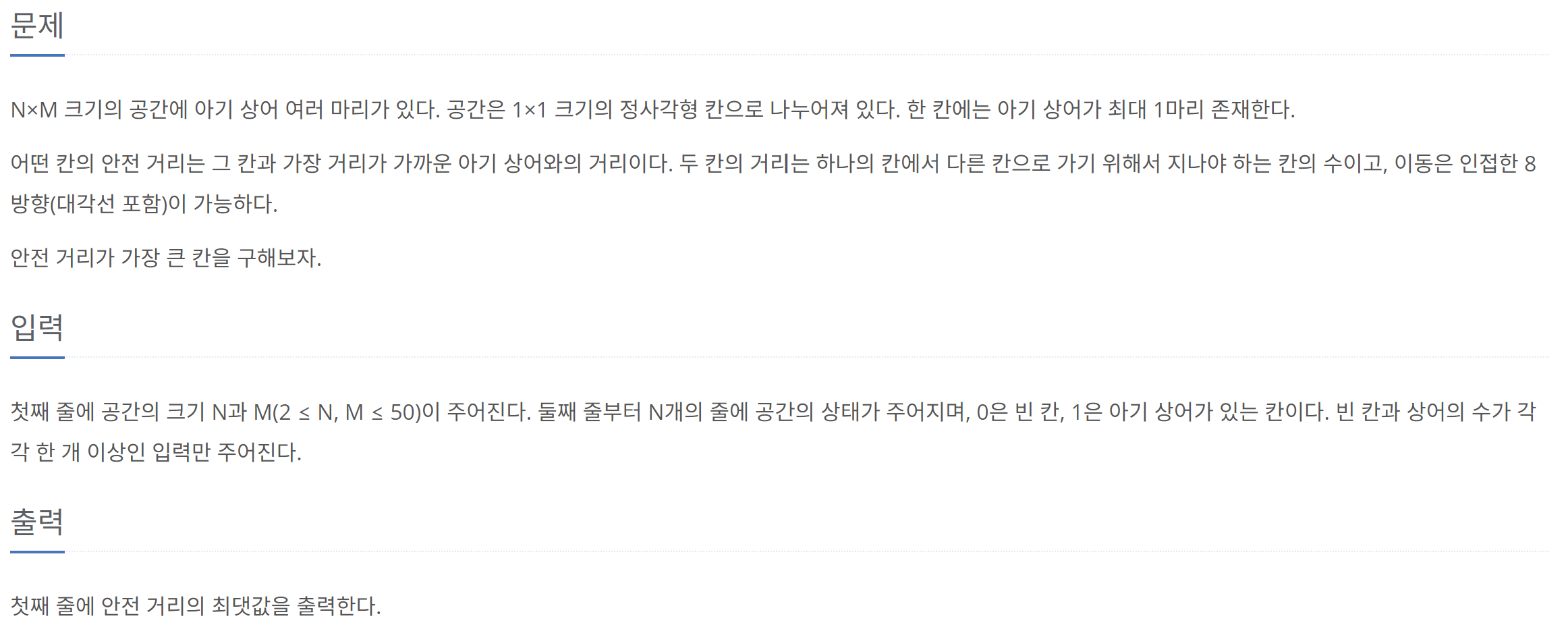
문제

접근 방법

큐의 모든 아기 상어의 위치를 집어넣어 주고 주변을 순차적으로 탐색한다고 생각해 보자.
그러면 모든 타일은 가장 가까운 아기 상어와의 거리가 될 것이다. (가장 가까운 타일부터 접근하기 때문에 그렇다)

코드

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct node
{
    int y, x;
};
int dy[] = {1, -1, 0, 0, 1, 1, -1, -1}, dx[] = {0, 0, 1, -1, 1, -1, 1, -1};
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int N, M, ret = 0;
    cin >> N >> M;
    vector<vector<int>> graph(N, vector<int>(M));
    queue<node> q;
    for (int i = 0; i < N; ++i)
        for (int j = 0; j < M; ++j)
        {
            cin >> graph[i][j];
            if (graph[i][j])
                q.push({i, j});
        }
    while (!q.empty())
    {
        node cur = q.front();
        q.pop();
        for (int i = 0; i < 8; ++i)
        {
            int ny = cur.y + dy[i];
            int nx = cur.x + dx[i];
            if (ny < 0 || nx < 0 || ny >= N || nx >= M || graph[ny][nx])
                continue;
            graph[ny][nx] = graph[cur.y][cur.x] + 1;
            ret = max(graph[ny][nx], ret);
            q.push({ny, nx});
        }
    }
    cout << ret - 1;
    return 0;
}

풀이

졸려서 아기 상어 기준으로 가장 가까운 아기 상어의 길이가 안전거리인 줄 알았다.

특정 칸을 기준으로 가장 가까운 아기 상어와의 거리이기에 BFS로 해결할 수 있다.