[C++][백준 6497] 전력난

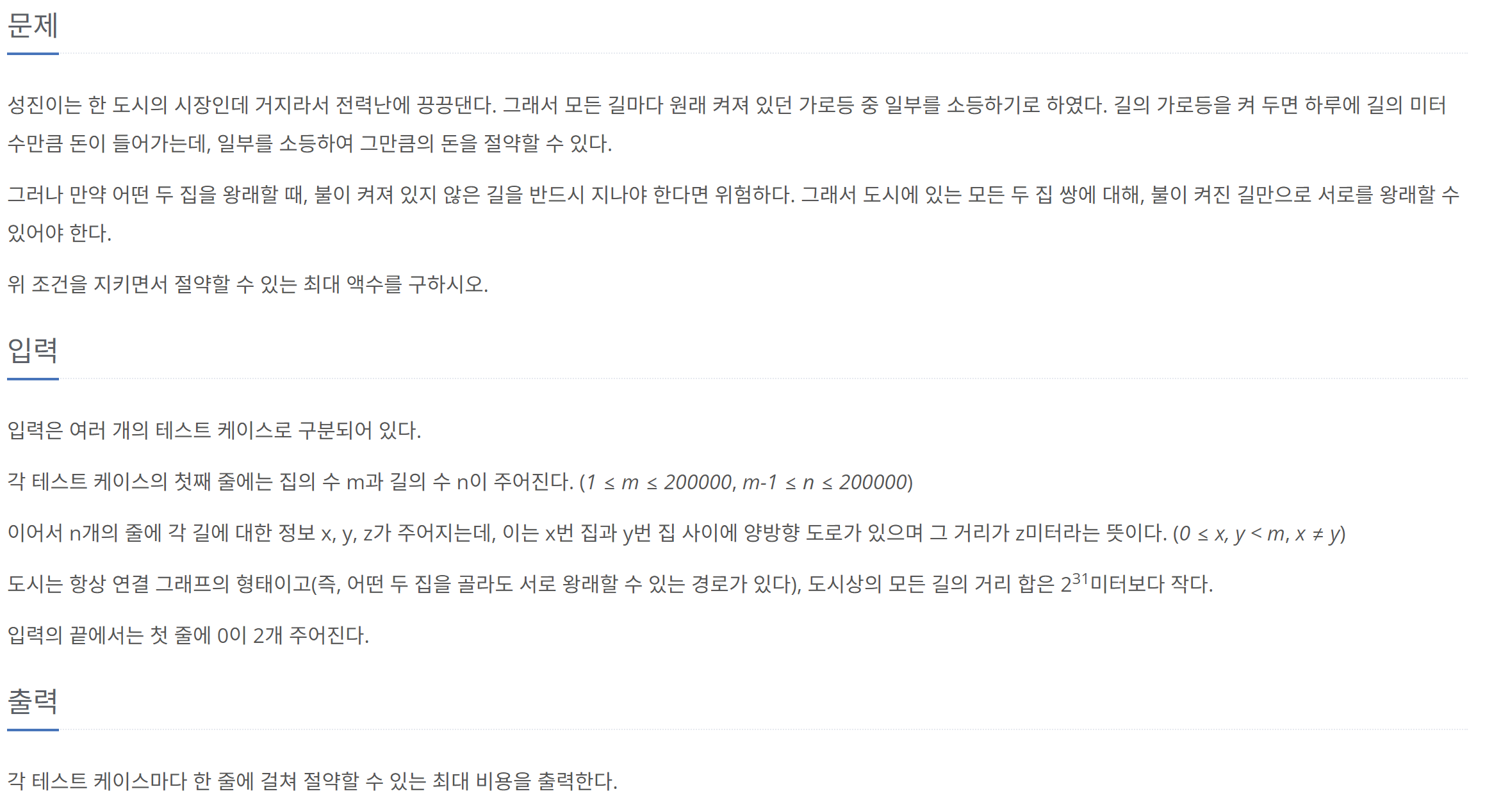
문제

접근 방법

무슨 소리인가 싶겠지만 모든 집을 연결해 주는 것이 목표이고 남은 간선은 절약했다는 셈 치는 것이다.

최소 신장 트리로 모든 집을 연결해 주고 남은 비용을 출력하면 된다.

코드

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#define MAX_M 200001
using namespace std;
typedef pair<int, int> pii;
int m, n, x, y, z, ret;
vector<pii> graph[MAX_M];
bool isVisited[MAX_M];
priority_queue<pii, vector<pii>, greater<pii>> pq;
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    while (cin >> m >> n)
    {
        memset(isVisited, false, sizeof(isVisited));
        ret = 0;
        for (int i = 0; i < m; ++i)
            graph[i].clear();
        if (m == 0 && n == 0)
            break;
        while (n--)
        {
            cin >> x >> y >> z;
            graph[x].push_back({z, y});
            graph[y].push_back({z, x});
            ret += z;
        }
        pq.push({0, 0});
        while (!pq.empty())
        {
            pii cur = pq.top();
            pq.pop();
            if (isVisited[cur.second])
                continue;
            isVisited[cur.second] = true;
            ret -= cur.first;
            for (pii next : graph[cur.second])
            {
                if (isVisited[next.second])
                    continue;
                pq.push(next);
            }
        }
        cout << ret << "\n";
    }
    return 0;
}

풀이

미리 모든 비용을 더해준 뒤 채용된 비용을 빼주면 절약할 수 있는 최대 비용이 구해진다.