파티 1238

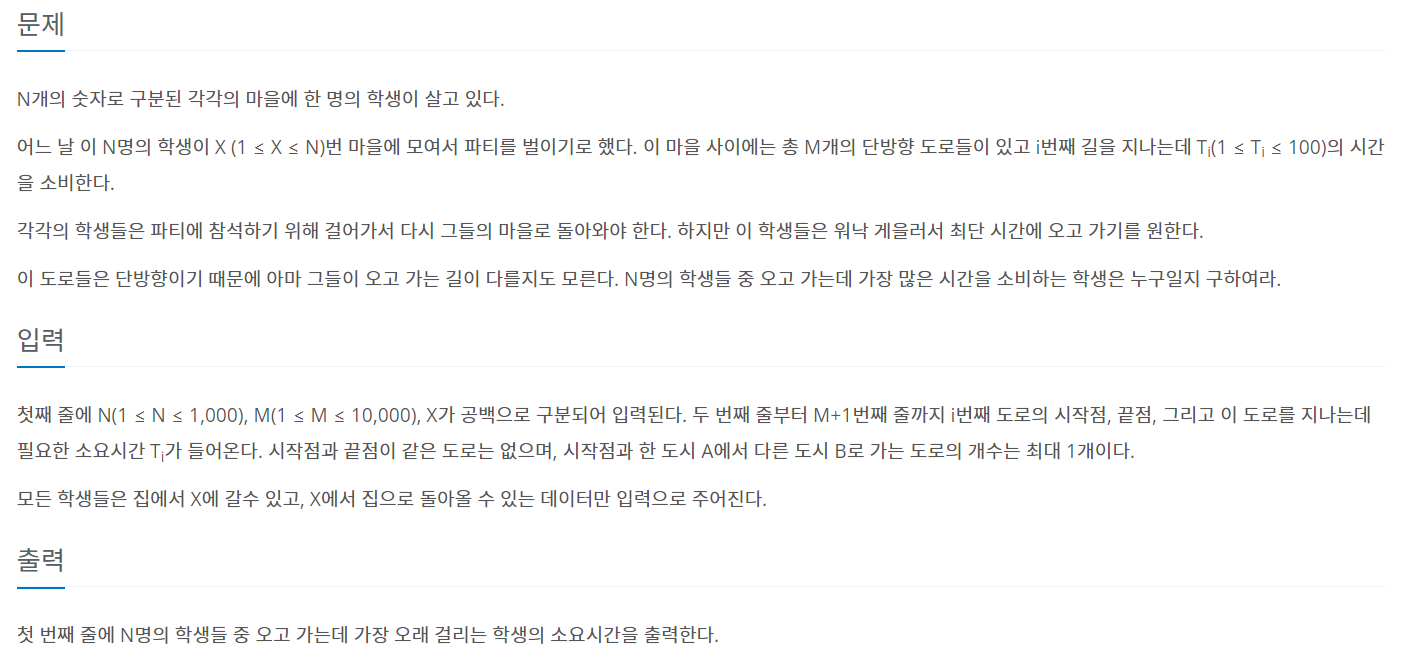
문제

접근 방법

잠결에 봐서 X를 들렀다 가는 것이 아닌 모든 마을을 들르는 것으로 봤다.
그래서 DFS를 통해 모든 마을을 들러 확인하는 방식을 사용하려다 틀렸다.
X를 들렀다가 돌아오는 것임을 알게 되고 X까지의 최솟값을 구한 뒤 다시 돌아오는 최솟값을 구하는 방법으로 해결하면 된다고 생각했다.

코드

#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>
#include <queue>
using namespace std;
vector<vector<vector<pair<int, int>>>> map;
vector<int> townDist, dist;
int N, M, X;
void Dijkstra(int i, int arrow)
{
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    dist = vector<int>(N + 1, INT_MAX);
    pq.push({0, i});
    dist[i] = 0;
    while (!pq.empty())
    {
        pair<int, int> cur = pq.top();
        pq.pop();
        if (dist[cur.second] < cur.first)
            continue;
        for (pair<int, int> j : map[arrow][cur.second])
        {
            if (dist[j.second] > dist[cur.second] + j.first)
            {
                dist[j.second] = dist[cur.second] + j.first;
                pq.push({dist[j.second], j.second});
            }
        }
    }
    for (int i = 1; i <= N; ++i)
    {
        townDist[i] += dist[i];
    }
}
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    cin >> N >> M >> X;
    int maxSum = 0;
    map = vector<vector<vector<pair<int, int>>>>(2, vector<vector<pair<int, int>>>(N + 1, vector<pair<int, int>>()));
    townDist = vector<int>(N + 1);
    for (int i = 0; i < M; ++i)
    {
        int start, end, time;
        cin >> start >> end >> time;
        map[0][start].push_back({time, end});
        map[1][end].push_back({time, start});
    }
    Dijkstra(X, 0);
    Dijkstra(X, 1);
    for (int i = 1; i <= N; ++i)
    {
        maxSum = max(maxSum, townDist[i]);
    }
    cout << maxSum;
    return 0;
}

풀이

제출하고 보니 각 점에서 다익스트라를 하고 X에서 다시 다익스트라를 하는 방법보다 역방향 그래프를 하나 더 만들어서 다익스트라를 2번 하는 것이 더 효율적인 것을 알게 됐다. (간단하게 생각해보면 x, y가 있고 x에서 y로 3, y에서 x로 2라 할 때 x와 y에서 따로 돌릴 수도 있지만 (x에서 y로 최소가 3, y에서 x로 최소가 2) 역방향 그래프를 두면 x를 기준으로 왔다 갔다 하는 것을 수행할 수 있다(x에서 y로 최소가 3, x로 오는 y가 최소가 2))
그래서 그렇게 수정하여서 제출하니 엄청난 시간 절약이 됐다.