[기본 수학 이론] 경우의 수 - 조합

조합

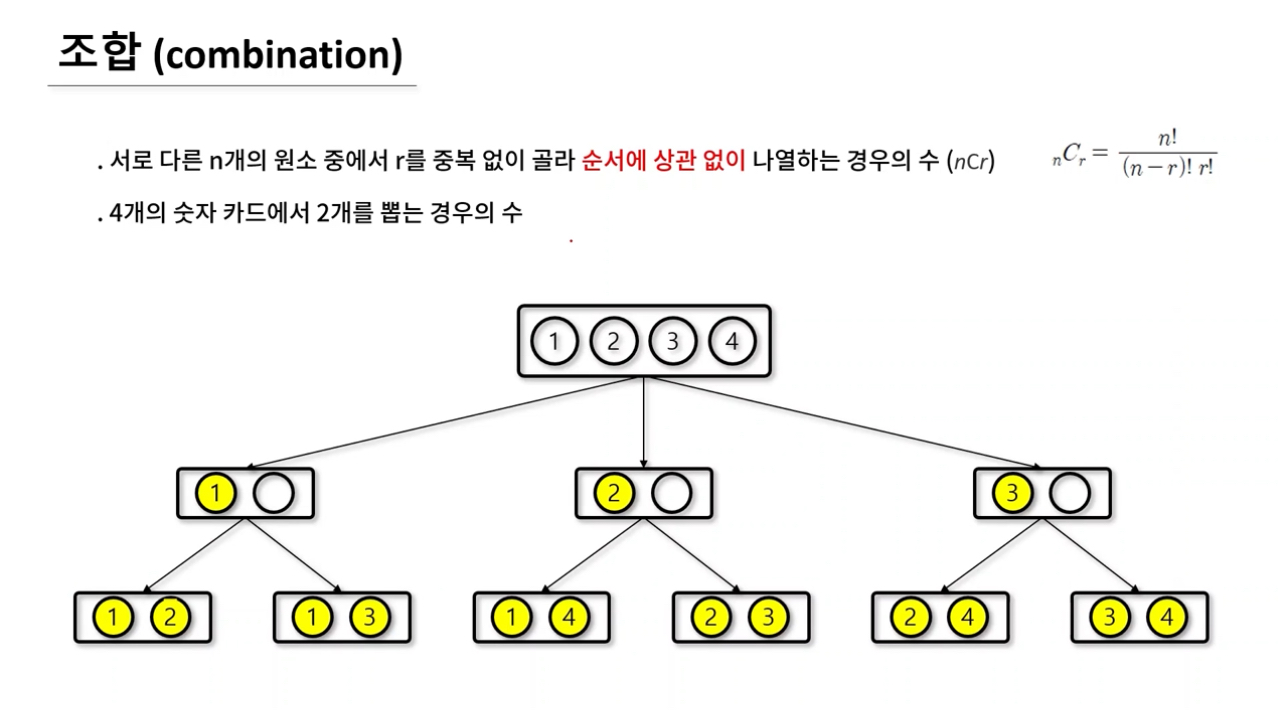
• 순서에 상관 없이 나열하기 때문에 [1,2] 와 [2,1]은 중복

for 반복문

let input = [1,2,3,4];
let count = 0;

function combination(arr){

  for(let i = 0; i< arr.length; i++){
    for( let j = i+1; j < arr.length; j++){
      count++;
      console.log(arr[i], arr[j]);
    }
  }
}

combination(input);
console.log(count);

• 첫 번째 요소를 고정하고 남은 요소에서 반복문을 돌리고
  다음 요소를 고정하고 또 남은 요소에서 반복문 돌리기

• 뽑아야하는 개수만큼 for 반복문의 수가 늘어나서 비효율적
  
  

재귀

let input = [1,2,3,4];
let output = [];
let count = 0;

function combination(arr, data, s, idx, r){
  	if( s == r){
      count++;
      console.log(data);
      return;
    }
  	
	for( let i = idx; arr.length - i >= r - s; i++){
    	  data[s] = arr[i]; 
      	combination(arr, data, s+1, i+1, r);
    }
}

combination(input,output, 0, 0, 2);
console.log(count);

• 빈 array에 기존 input 배열의 요소를 하나씩 뽑아 저장
• s = r개 중 현재 뽑는 회차의 인덱스 (2개를 뽑는 경우: 0, 1이 됨)
• i = 기존 input 배열에서 뽑는 수의 인덱스
• idx = loop를 돌면서 뽑을 요소의 시작 인덱스 업데이트

arr.length - i >= r - s

ex) [1,2,3,4]에서 2개를 뽑는 경우

1. s는 output 배열의 각 요소의 인덱스 표현
2. r - s는 output 배열의 인덱스 범위
3. arr.length - i는 arr배열에서 i의 범위
4. 늘 뽑는 개수는 arr 배열의 길이와 같거나 작아야 한다.
   
   

처음에 i의 범위 설정을 두고서 한참을 생각했다.
그리고 재귀를 타고 들어가면서 인덱스가 어떻게 업데이트 되고
어떤 인자(s, i, idx ?)를 업데이트 해야 하는지가 가장 헷갈렸다


재귀를 반복해서 공부 해야겠다