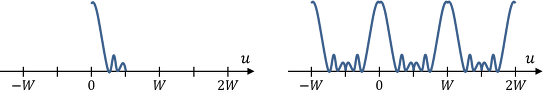푸리에 변환

푸리에 변환 (Fourier transform, FT)은 시간이나 공간 영역에 함수를 시간 또는 주파수 성분으로 분해하는 변환.

함수 $x(t)$가 복소수 범위로 정의되어 있을 때, 푸리에 변환 $X(\xi)$는 다음과 같음.
$X(\xi)=\int_{-\infin}^{\infin}x(t)e^{-2\pi i\xi t}dt$ ($t$: 시간, $\xi$: 주파수)

푸리에 변환은 복잡한 모양의 주기 함수를 사인와 코사인으로 분해.
오일러 공식을 통해 사인과 코사인의 분해를 $e^{2\pi i\theta}$로 표현.
즉, $e^{2\pi j\theta}=cos(2\pi\theta)+isin(2\pi\theta)$

오일러 공식 (Euler's formula)
$e^{ix}=cosx+isinx$

푸리에 변환은 입력 신호가 어떤 신호이든지 상관없이 사인과 코사인 주기 함수들의 합으로 항상 분해할 수 있음.

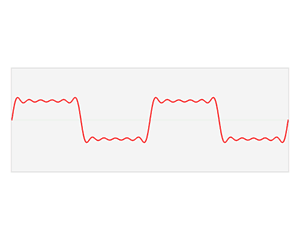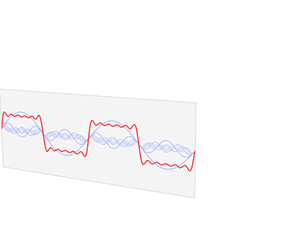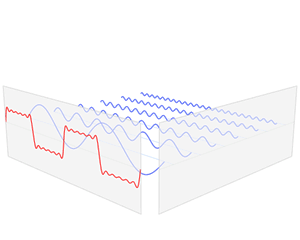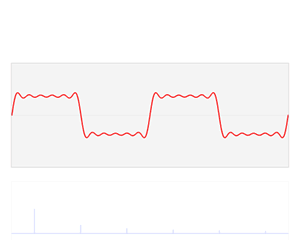
시간 또는 공간 domain을 푸리에 변환을 통해 주파수 domain으로 변환.

푸리에 변환의 수식은 다음과 같음.
(1) Fourier Transform
$F(u)=\int_{-\infin}^{\infin}f(x)e^{-j2\pi ux}dx$
(2) Inverse Fourier Transform
$f(x)=\int_{-\infin}^{\infin}F(u)e^{j2\pi ux}du$
($f(x)$: 임의의 입력신호, $e^{j2\pi ux}$: 주파수가 $u$인 주기함수, $F(u)$: 주기함수의 계수)

오일러 공식 적용
$e^{j2\pi ux}=cos(2\pi ux)+jsin(2\pi ux)$ (주파수: $u$)

2차원 푸리에 변환

이미지 처리에 푸리에 변환을 활용하기 위해서는 2차원 푸리에 변환이 사용.
공간 domain을 공간 주파수 (spatial frequency) domain으로 변환.
$x$축$,$ $y$축 방향으로의 주파수를 $u,v$라 할 때,
(1) 2D Fourier Transform
$F(u,v)=\int_{-\infin}^{\infin}\int_{-\infin}^{\infin}f(x,y)e^{-j2\pi(ux+vy)}dxdy$
(2) 2D Inverse Fourier Transform
$f(x,y)=\int_{-\infin}^{\infin}\int_{-\infin}^{\infin}F(u,v)e^{j2\pi(ux+vy)}dudv$
($F(u,v)$: $x$축$,$ $y$축 방향으로의 주파수가 $u,v$인 주기함수의 계수)

이미지는 이산 (discrete)신호이며, 유한한 구간에서 정의되기 때문에,
이미지 $W\times H$에 대해서
(1) 2D Discrete Fourier Transform
$F(u,v)=$$1\over WH$$\Sigma_{x=0}^{W-1}\Sigma_{y=0}^{H-1}f(x,y)e^{-j2\pi(ux/W+vy/H)}$
(2) 2D Inverse Discrete Fourier Transform
$f(x,y)=\Sigma_{u=0}^{W-1}\Sigma_{v=0}^{H-1}F(u,v)e^{j2\pi(ux/W+vy/H)}$
($F(u,v)$: $x$축$,$ $y$축 방향으로의 주파수가 $u/W,v/H$인 주기함수의 계수)

$F(u,v)$는 복소수이므로, $F(u,v)=Real(u,v)+jImag(u,v)$로 표현.
복소평면 내에서 $(Real(u,v),Imag(u,v))$ 좌표로 표현.
Magnitude
$\vert F(u,v)\vert=(Real^2(u,v)+Imag^2(u,v))^{1/2}$
Phase
$\phi(u,v)=arctan(Imag(u,v)/Real(u,v))$

푸리에 스펙트럼

푸리에 스펙트럼은 해당 주파수 성분이 입력 이미지에 얼마나 강하게 포함되어 있는지를 나타냄.
즉, magnitude $\vert F(u,v)\vert$를 픽셀값으로 표현.

(a)
입력 이미지를 $f(x,y)$로 표현.
$x\in[0,W-1],\ y\in[0,H-1]$.
(b)
$xy$-좌표계를 $uv$-좌표계로 좌표 변환.
픽셀값으로 magnitude $\vert F(u,v)\vert$를 사용.
$u\in[0,W-1],\ v\in[0,H-1]$.
푸리에 변환 시에 저주파 영역은 매우 큰 값을 갖지만 다른 영역은 0에 가까운 값을 갖기 때문에, $log$를 씌움.
(c)
$\vert F(u,v)\vert$의 특징으로 주기성과 대칭성이 있으므로 다음과 같음.

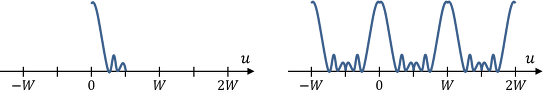
즉, 원점에 대해 대칭이면서 $u=W/2,\ v=H/2$에 대해서 대칭.
따라서 $u\in[0,W],\ v\in[0,H]$를 $u\in[-W/2,W/2],\ v\in[-H/2,H/2]$로 이동.

Properties of the Fourier Transform
$F(u,v)=$$1\over WH$$\Sigma_{x=0}^{W-1}\Sigma_{y=0}^{H-1}f(x,y)e^{-j2\pi(ux/W+vy/H)}$

(1) Periodicity
$F(u+W,v+H)$
$=$$1\over WH$$\Sigma_{x=0}^{W-1}\Sigma_{y=0}^{H-1}f(x,y)e^{-j2\pi((u+W)x/W+(v+H)y/H)}$
$=$$1\over WH$$\Sigma_{x=0}^{W-1}\Sigma_{y=0}^{H-1}f(x,y)e^{-j2\pi(ux/W+vy/H)}e^{-j2\pi(x+y)}$
$=$$1\over WH$$\Sigma_{x=0}^{W-1}\Sigma_{y=0}^{H-1}f(x,y)e^{-j2\pi(ux/W+vy/H)}\times1$ (∵ Euler's Identity)
$=F(u,v)$

(2) Complex Conjugate Symmetry
$\vert F(u,v)\vert=\vert F(-u,-v)\vert$

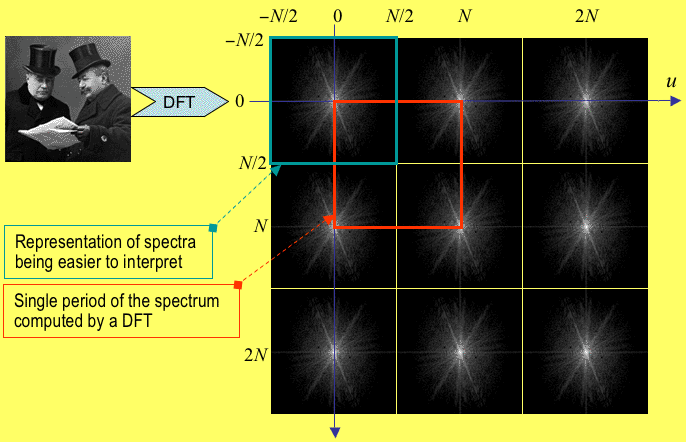
해당 그림에서 볼 수 있듯이 $[0,N]$까지의 이미지를 shift하여 $[-N/2,N/2]$를 사용.
이는 원점이 저주파 계수이고 원점으로부터 멀어질수록 고주파 계수이므로, 분석에 용이.

Fourier Bases

푸리에 변환의 bases는 정현파.

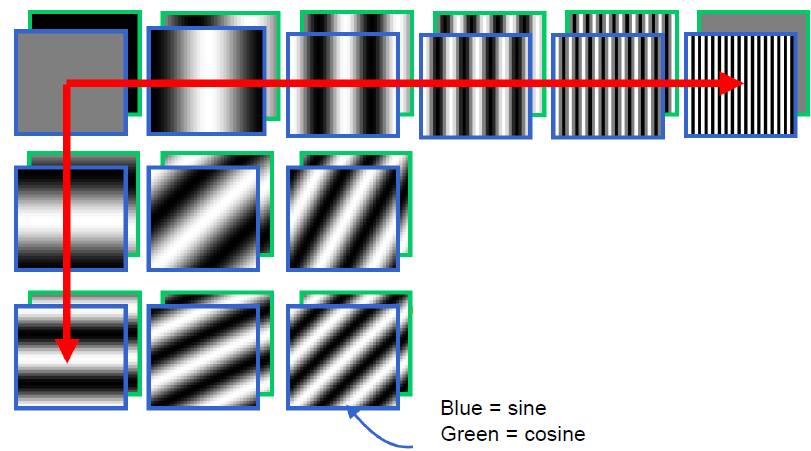
(1) $u$축
$x$축 방향으로의 정현파만 존재.
이는 원본 이미지가 수평 방향으로만 신호가 존재.
원점에서 멀어질수록 주파수 $u$값이 커지므로, 신호의 간격이 좁아짐.

(2) $v$축
$y$축 방향으로의 정현파만 존재.
이는 원본 이미지가 수직 방향으로만 신호가 존재.
원점에서 멀어질수록 주파수 $v$값이 커지므로, 신호의 간격이 좁아짐.

(3) Rotation
푸리에 변환은 rotation을 보존하므로 $uv$-좌표계를 회전하여, spectrum을 분석.

---

Reference
푸리에 변환
Fourier Transform(푸리에 변환)의 이해와 활용
Spatial Frequency Domain
[비전5] Frequency and Image
The Fourier Transform
How to Create Any Image Using Only Sine Functions | 2D Fourier Transform in Python