[python]부분합

들어가며

이글은 동빈나님의 이코테 강의를 보며 정리한 글입니다.

부분합

다음과 같은 배열이 존재한다고 하겠습니다.

[1, 2, 3, 4, 5] 이 배열을 통하여 우리는 시작점과 끝점을 입력받아 해당 구간의 합을 구해야 된다고 하겠습니다. 그러한 경우 우리는 선형탐색을 통하여 시작점과 끝점까지의 값을 더하여 결과로 출력할 수 있을 것입니다. 그렇다면, 그러한 작업을 여러번 수행하게 된다면 어떻게 될까요?

배열의 크기를 $N$, 그러한 구간의 개수를 $M$이라고 한다면 구간마다 최대 $N$번의 선형탐색을 수행할 것이고, 그러한 작업을 $M$번 반복하므로 $O(N\times M)$라고 할 수 있을 것입니다. 이는 $N, M$의 크기에 따라 굉장히 비효율적일 수 있습니다. 이를 개선하기 위해서 우리는 부분합을 이용할 수 있습니다.

입력받은 배열의 값을 전위부터 더하여 끝지점까지의 합으로 할당하는 것인데요. 위의 배열을 예시로 부분합을 표현하면 아래와 같습니다.

[1, 3, 6, 10, 15]

1번값은 1번까지의 합을 표현, 2번값은 2번까지의 합 이렇게 마지막 인덱스까지의 합으로 배열을 완성할 수 있으며 우리는 이를 누적합(Prefix Sum)이라고 할 수 있습니다. 이렇게 완성한 누적합을 통하여 구간합을 알 수 있는데요. 만약 3번부터 5번까지의 합을 알고 싶다면 아래와 같은 연산을 이용해 값을 구할 수 있습니다.

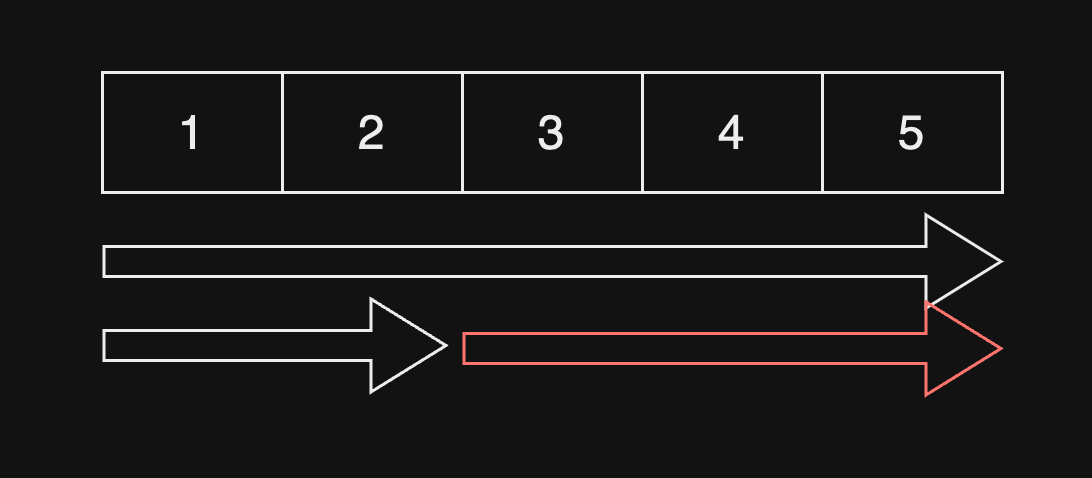
이렇게 되면 3번부터 5번까지 구간을 구간쿼리라고하고, 5번까지의 합에서 2번까지의 합을 빼면 3번부터 5번까지의 구간합을 구할 수 있는 것입니다.

부분합 예시

실제로 위의 부분합을 예시로 코드를 작성하겠습니다.

# 배열의 크기
n = 5
# 배열
arr = [1, 2, 3, 4, 5]
# 전위합
psum = [0] * (len(arr)+1)
for i in range(1, n+1):
    psum[i] += arr[i-1] + psum[i-1]
print(*psum)

>> 1, 3, 6, 10, 15

실제 코드에서 부분합을 구하는 것은 부분합 배열의 0번 인덱스는 제외하고 1번 인덱스부터 수행을하는데, 이는 범위에러를 방지하기 위해서입니다. 그리고 부분합을 구하면서 총 $N$번, 그리고 $M$번의 쿼리 연산을 수행하기 때문에 $O(N+M)$의 시간복잡도를 갖게 됩니다. 시간이 대폭 줄어드는 것이죠.