[python]우선순위 큐

들어가며

이글은 동빈나님의 이코테 강의를 보며 정리한 글입니다.

Complete Binary Tree

완전 이진 트리란 루트 노드부터 시작하여 왼쪽 자식, 오른쪽 자식 순으로 데이터가 삽입되는 트리를 의미합니다.

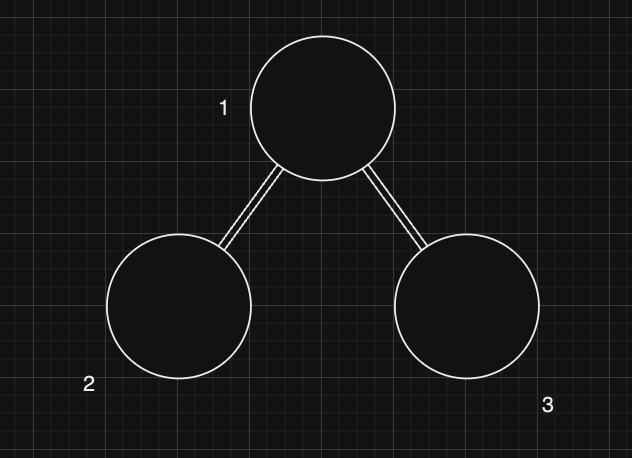
이러한 트리에서는 가장 위인 루트 노드부터 왼쪽, 오른쪽 순으로 데이터가 차례대로 삽입됩니다.

Heap

힙은 완전 이진 트리 자료구조의 일종으로, 항상 루트 노드를 제거합니다. 여기서 힙의 루트 노드 값의 기준에 따라서 최소 힙(min heap), 최대 힙(max heap)으로 구분할 수 있습니다.

최소힙은 단순하게 루트노드에 가장 작은 값을 가진 힙으로, 작은 순서대로 데이터가 제거되는 구조입니다. 반면에 최대힙은 가장 큰 값이 루트 노드 값이고, 큰 값부터 제거됩니다.

이러한 경우 최소힙과 최대힙은 단순하게 삽입하고 다시 빼내는 작업을 반복할 경우, 오름차순 혹은 내림차순 정렬된 효과를 볼 수 있습니다.

Heapify

Heapify는 힙을 구성하는 함수를 의미합니다. 최소힙 혹은 최대힙을 힙으로 구성하기 위해서는 Heapify 함수를 통해서 현재의 데이터의 값과 그 트리의 루트노드의 데이터값을 비교하면서 조건에 맞지 않은 경우 자리를 바꿔가며 최소힙, 최대힙을 구성할 수 있게 해줍니다.

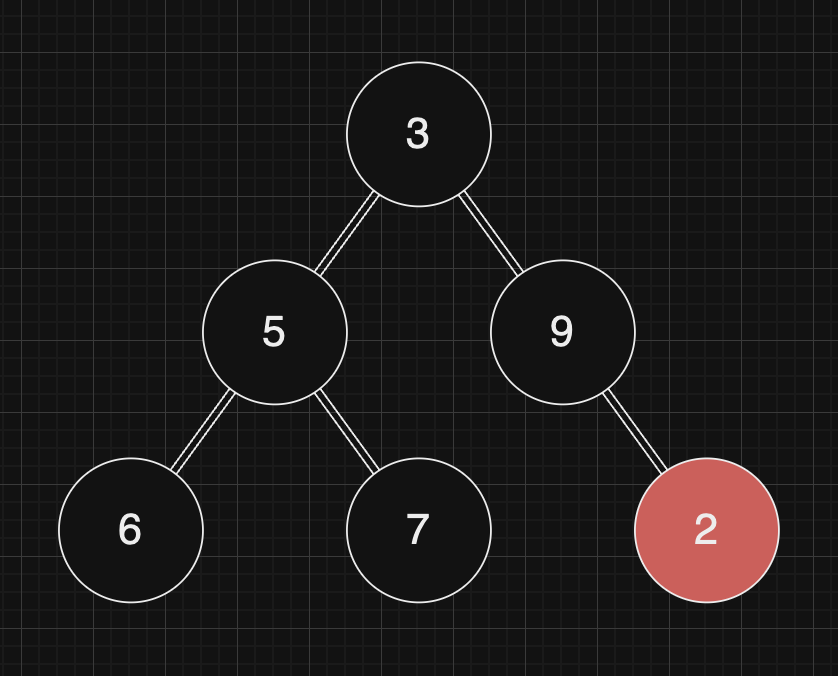
자, 예를 들어 2라는 데이터가 위의 힙에 들어온 경우, Heapify를 통해서 최소힙을 만족시킨다고 할 경우, 2는 그 위의 데이터인 9와 비교하고 자리를 바꾸고, 다시 위의 3과 비교하여 자리를 바꾸면서 단 두번만에 최소힙을 유지시켜줍니다. 이러한 경우 비교하는 대상은 루트 노드의 데이터이므로 시간복잡도는 빅오 표기법을 이용해서 $O(logN)$의 시간복잡도를 가집니다.

제거하는 경우에도 제거할 데이터와 가장 큰 데이터의 자리를 바꾸고, Heapify를 수행하면 되므로 $O(logN)$의 시간복잡도를 가집니다. 이로써, 삽입과 제거 시간복잡도는 같습니다.

Priority Queue

우선순위 큐는 가장 우선순위가 높은 데이터를 가장 먼저 삭제하는 자료구조입니다. 기본적으로 큐 자료구조와 굉장히 흡사하지만, 삭제되는 데이터가 다르다는 차이가 있습니다.

파이썬으로 Priority Queue 구현하기

파이썬에서 우선순위 큐는 단순하게 리스트 자료형을 이용해서 구현할 수도 있고, 힙을 사용해서 구현할수도 있습니다.

하지만, 리스트를 이용해서 구현하는 경우 삭제할 때, 모든 자료형을 확인해야 하므로 삽입과 삭제가 각각 $O(1), O(N)$의 시간복잡도를 갖게 됩니다. 그렇기 때문에 삽입과 삭제 모두 $O(logN)$의 시간복잡도를 가지는 힙 자료구조를 이용해서 구현할 수 있습니다.

파이썬에서는 heapq 라이브러리를 사용해서 구현할 수 있는데, 해당 라이브러리는 최소힙을 이용합니다.

파이썬으로 구현

파이썬으로 최소힙을 구현해보겠습니다.

import heapq

arr = [3, 1, 6, 7, 9]
h = []
for i in arr:
    heapq.heappush(h, i)

print(heapq.heappop(h))
print(heapq.heappop(h))
print(heapq.heappop(h))
print(heapq.heappop(h))
print(heapq.heappop(h))

>> 1
>> 3
>> 6
>> 7
>> 9

이 예제는 리스트 데이터를 최소힙으로 구성하는 예제입니다. 리스트 자료형의 3, 1, 6, 7, 9가 차례대로 힙에 heappush 함수를 통해서 입력됩니다. 이러한 경우 자연스럽게 heapify가 수행됩니다. 다 끝난 후 결과를 확인하면 가장 루트 노드에 1이 있으므로 1이 출력됩니다.