
들어가며
이글은 동빈나님의 이코테 강의를 보며 정리한 글입니다.
이전에 알아본 DFS, BFS는 그래프 탐색 알고리즘입니다. 그러나, 그래프가 아닌 선형데이터를 탐색할 수도 있지요. 그럴 경우에는 순차 탐색 혹은 이진 탐색 알고리즘을 사용할 수 있습니다.
순차 탐색
순차 탐색은 말 그대로 선형데이터를 앞에서부터 하나씩 확인하는 방법입니다. 1부터 9까지 존재하는 배열에서 8을 찾기 위해 순차 탐색한다고 하겠습니다. 가장 먼저 맨 처음 데이터인 1을 확인합니다.
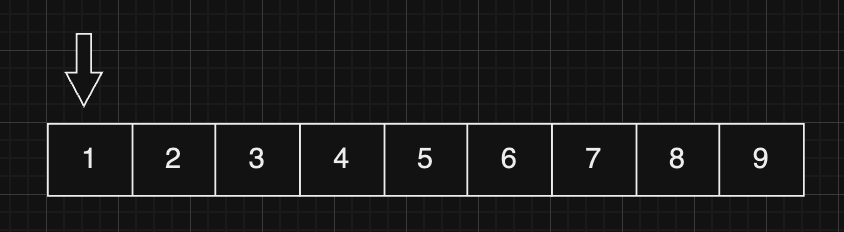
이제 1은 8이 아닙니다. 이제 다음 데이터를 확인합니다.
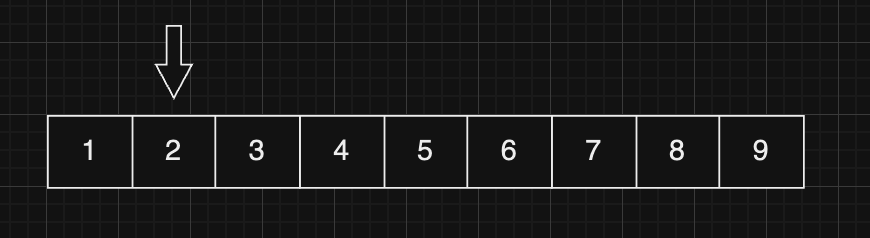
2역시 8과 같지 않습니다. 이렇게 순서대로 확인하다가 8번째에서 8을 찾을 수 있습니다.
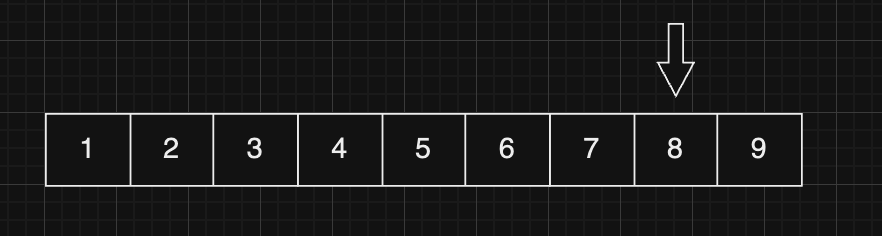
이 경우에는 데이터의 갯수 에 따라서 빅오 표기법으로 의 시간복잡도를 가집니다.
이진 탐색
이진 탐색은 순차 탐색과 다르게 시작점과 끝점, 그리고 중간점을 이용해서 탐색합니다. 마찬가지로 1부터 9까지 존재하는 배열에서 8을 찾는다고 하겠습니다.

이진 탐색에서는 시작점과 끝점을 이용해서 중간점을 찾을 수 있습니다. 이 배열에서 0번 인덱스 값인 1과 8번 인덱스값인 9는 각각 시작점과 끝점이라고 할 수 있습니다. 이 때, 각 인덱스의 합을 2로 나눈 값인 인덱스가 중간점이됩니다.
이경우에는 (0+8)/2 이므로 4번 인덱스 값인 5가 중간값이 됩니다. 찾고자 하는 값인 8은 중간점인 값인 5보다 크므로 중간점을 포함해서 왼쪽의 데이터들은 볼 필요가 없습니다. 그리고 이렇게 되면 시작점과 끝점을 다시 정의하게 됩니다.

남은 데이터중 가장 첫번째인 5번 인덱스가 시작점이 됩니다. 끝점은 이전과 동일해요. 그리고 5번 인덱스와 8번 인덱스의 중간점은 (5+8)/2=6.5 지만, 소숫점은 버림하여 6번 인덱스가 중간값이 됩니다.
역시나 중간값보다 8이 더 크므로 중간값의 왼쪽 데이터들은 모두 없앱니다.

자, 남은 데이터 중 가장 첫번째인 7번 인덱스의 값 8이 시작점, 끝점은 동일합니다. 중간값은 (7+8)/2 =7.5입니다. 소숫점은 버리기 때문에 7번 인덱스가 시작점인 동시에 중간점이 됩니다.
이 경우에는 중간점과 찾고자하는 값이 동일하므로 탐색을 종료하게 됩니다.
자, 순차탐색과 다르게 탐색범위를 계속해서 절반으로 줄이기 때문에 시간복잡도는 를 보장합니다.
이제, python코드로 작성된 이진탐색을 알아보겠습니다.
def binary_search(array, target, start, end):
# 시작점이 끝점보다 큰 경우엔 값이 존재하지 않음
if start>end:
return None
mid = (start+end) // 2
# 값을 찾은 경우
if array[mid] == target:
return mid
# 중간값보다 왼쪽에 있는 경우
elif array[mid] > target:
return binary_search(array, target, start, mid-1)
# 중간값보다 오른쪽에 있는 경우
elif array[mid] < target:
return binary_search(array, target, mid+1, end)
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
result = binary_search(arr, 8, 0, 8)
if result == None:
print("존재하지 않음")
else:
print(result+1)python에서 이진 탐색은 재귀함수를 통해서 구현할 수 있습니다. 가장 먼저 시작점이 끝점보다 큰 경우에는 목표값이 존재하지 않는 경우입니다. 이런 경우에는 None을 반환해줍니다.
중간값과 목표값이 같은 경우에는 값을 찾은것이기 때문에 중간값을 반환합니다. 그 외에 경우에는 끝점 혹은 시작점을 수정한 후 재귀함수를 호출하면 됩니다.
여기서 반환되는 중간점의 값은 인덱스이므로 출력은 결과에서 +1한 값을 출력하면 됩니다.
