1749. Maximum Absolute Sum of Any Subarray
https://leetcode.com/problems/maximum-absolute-sum-of-any-subarray/
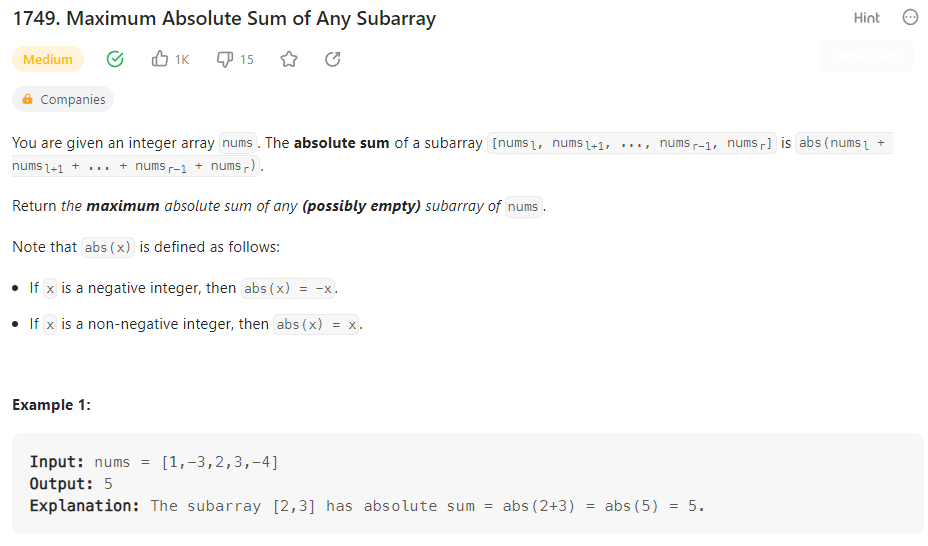
문제
풀이(DP_처음)
(Example 1 -> nums = [1, -3, 2, 3, -4])
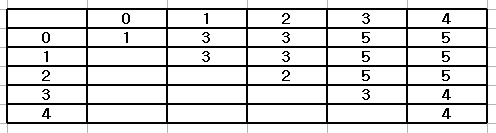
DP 테이블이다.
첫 번째로는 길이가 1일 때에는 abs(nums[i]]) 즉 절대값을 저장한다.
그 이후부터는 이전 max(dp[i-1][j], dp[i][j+1], abs(sum([i:j+1]))값을 저장한다.
결과(DP)
문제에서 nums 길이가 10^5라고 명시하였다. 위에 코드는 n^2 시간복잡도를 가지므로 상당히 좋지 않는 알고리즘이다.
풀이(DFS_두번째)
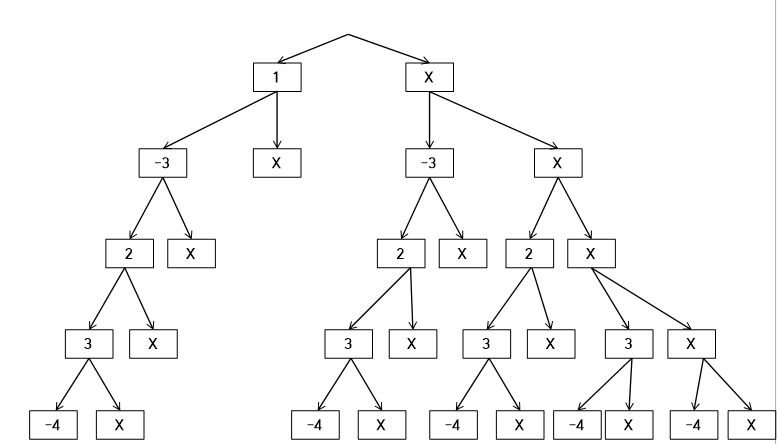
선택할 수 있는 경우의 수는 숫자를 선택할지 선택하지 않을지이다.
선택을 하게 되면 nums[i]를 더해주고 선택하지 않을 때에는 아무것도 더해주지 않는다. 그리고 재귀함수 인자에 더한 total값을 인자로 넘겨주어 위에서 부터 합이 계산되도록 한다.
즉 X -> X -> 2 -> 3 -> X라고 하였을 때 total은 0 -> 0 -> 2 -> 5 -> 5가 되는 것이다. 이제
계산된 total의 최대값을 구하면 된다.
ans는 현재 최대값을 저장하는 변수이고 리턴조건으로는 point가 len(nums)가 될 때 리턴해준다. 그리고 숫자 -> X 경로는 SubArray 조건이 아니므로 리턴해주어야 하는데 isTwo는 두번째 전값, isOne는 첫번째값이다. 숫자면 True, 아니면 False가 된다.
위에 DP테이블 풀이(N^2)보단 테스트케이스를 많이 통과했지만 아직까지도 TLE가 발생하였다. 여기서 찾아본 알고리즘이 카데인 알고리즘이다.
카데인 알고리즘
nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]가 주어졌을 때 부분배열의 최대합 문제를 구할 때 사용하는 알고리즘이다.
cursum = max(cursum + nums[i], nums[i])
maxsum = max(cursum, maxsum) 이다.
이것을 코드로 나타내면 다음과 같다.
이 알고리즘을 사용하면 (N) 시간복잡도로 구할 수 있다.
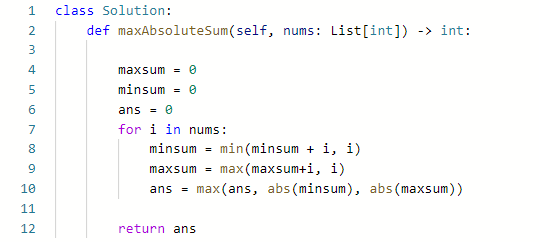
풀이(카데인 알고리즘)
위에 카데인 알고리즘을 응용한 풀이이다. 여기서 알아야 할 것은 절대값이 포함되어 있으므로 가장 최소일 때(음수일 때) 가장 클 때(양수일 때)를 비교해야 한다. 그 이유는 음수일 때 가장 작은 값을 abs를 할 경우 가장 클 수 있기 때문에 가장 최소일 때, 가장 클 때를 비교해야 한다.결과(카데인 알고리즘)