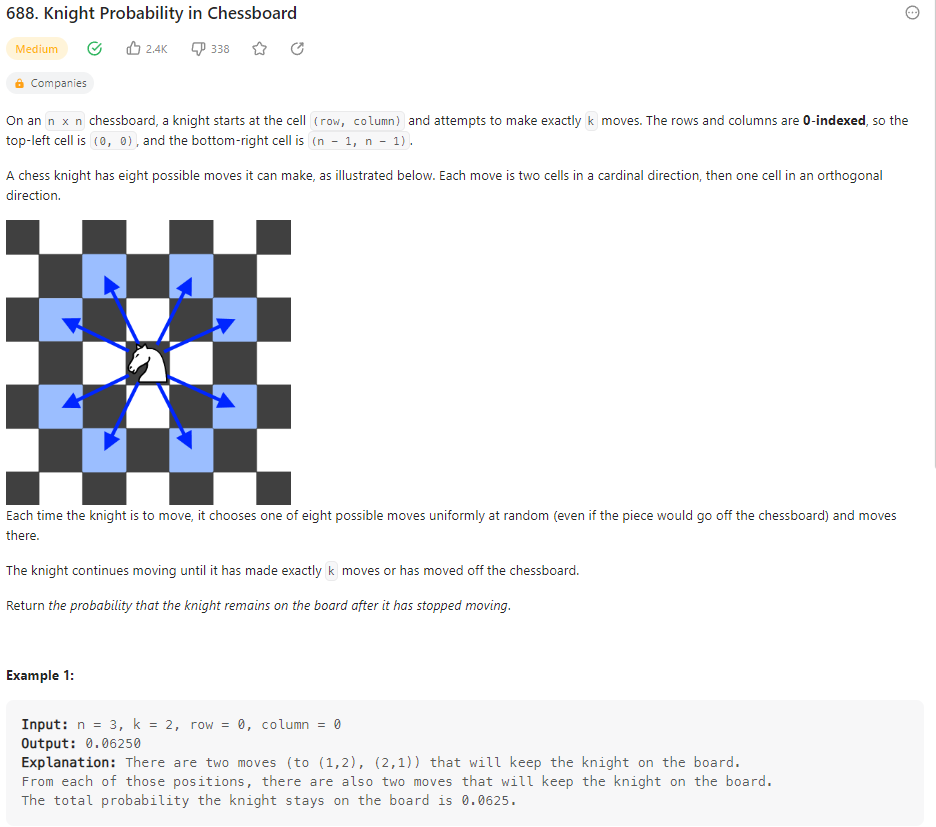
688. Knight Probability in Chessboard
https://leetcode.com/problems/knight-probability-in-chessboard/
문제
풀이(DFS)
k = 1일 때 가능한 경우의 수는 8 = 8이다
k = 2일 때 가능한 경우의 수는 8 * 8 = 64이다.
즉 k = n일 때 8 ^ n의 경우의 수를 가진다.
이제 해당 경우의 수에서 보드판 위에 있는 경우의 수를 구하면 된다.
문제에서 움직일 수 있는 경우의 수 8개로 주어줬고 움직일 수 있는 경우를 코드로 나타내면
one = dfs(row + 1, col + 2, depth + 1)
two = dfs(row + 2, col + 1, depth + 1)
three = dfs(row + 2, col - 1, depth + 1)
four = dfs(row + 1, col - 2, depth + 1)
five = dfs(row - 1, col + 2, depth + 1)
six = dfs(row - 2, col + 1, depth + 1)
seven = dfs(row - 2, col - 1, depth + 1)
eight = dfs(row - 1, col - 2, depth + 1) 과 같다.
이제 k번 움직인 후 row, col이 보드판 위에 없다면 0을 리턴 보드판 위에 있다면 1을 리턴한다.
이것을 코드로 나타내면 다음과 같다.

만약 k번 움직이는 동안 보드판 위에 나간다면 바로 리턴 0을 해주고 k번 움직였을 때 보드판 위에 있다면 1을 리턴한 후 더한 값을 반환하면 보드판 위에 있을 경우의 수를 반환한다.
그 후 총 경우의 수를 나누어 주면 확률을 반환하게 된다.
결과(DFS)