799. Champagne Tower
https://leetcode.com/problems/champagne-tower/
문제
풀이(BFS)
poured = 10이라고 가정했을 때 그래프를 그리면 다음과 같다.
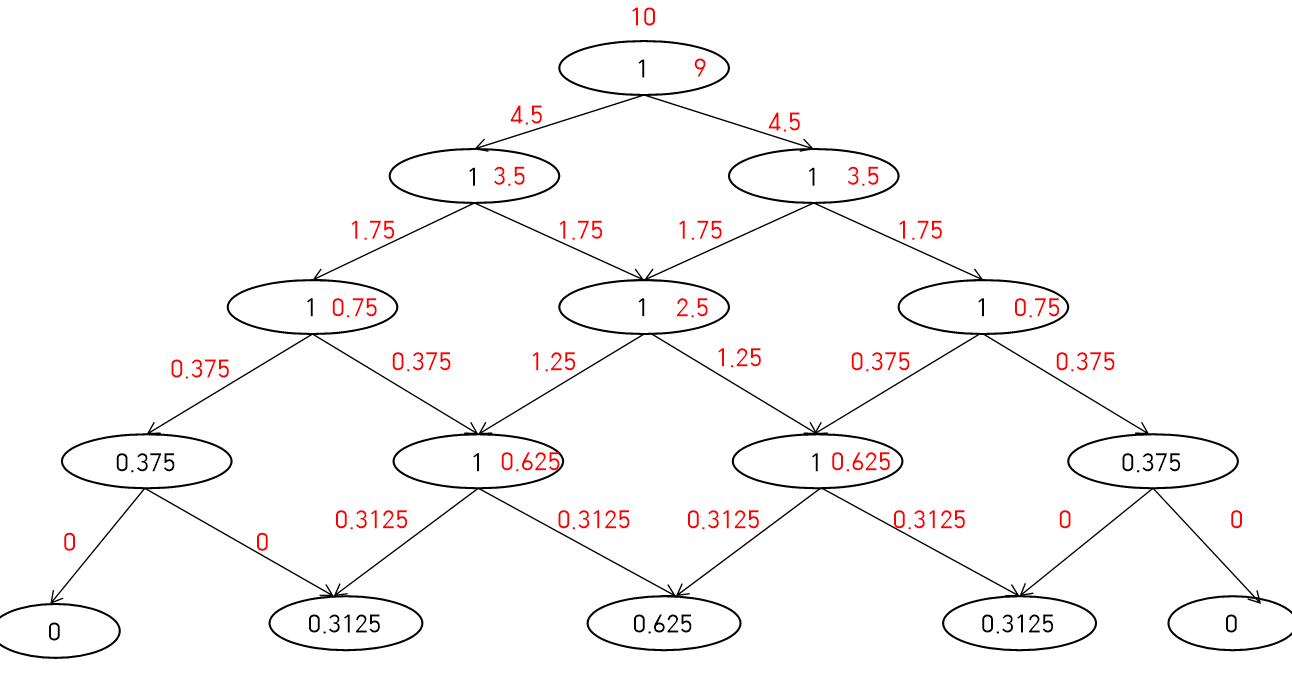
(첫 번째줄)
row = 0, col = 0 즉 맨 윗잔이 채워지면 10-1이 되어 남은 poured는 9가 되고 양쪽으로 4.5만큼 떨어진다.
(두 번째 줄)
row = 1, col = 0에서 잔을 채우면 3.5가 남고 양 옆으로 절반인 1.75씩 떨어진다.
row = 1, col = 1에서도 마찬가지로 3.5가 남고 양 옆으로 절반인 1.75씩 떨어진다.
(세 번째 줄)
row = 2, col = 0에서 잔을 채우면 0.75가 남고 양 옆으로 절반인 0.375씩 떨어진다.
row = 2, col = 1에서 잔을 채우면 2.5가 남고 양 옆으로 1.25씩 떨어진다.
row = 2, col = 2에서 잔을 채우면 0.75가 남고 양 옆으로 절반인 0.375씩 떨어진다.
(네 번째 줄)
row = 3, col = 0에서 1보다 작으므로 떨어질 수 없고 0.375가 남아 있는다.
row = 3, col = 1에서 잔을 채우면 0.625가 남고 양 옆으로 0.3125씩 떨어진다.
row = 3, col = 2에서 잔을 채우면 0.625가 남고 양 옆으로 0.3125씩 떨어진다.
row = 3, col = 3에서 1보다 작으므로 떨어질 수 없고 0.375가 남아 있는다.
(다섯 번째 줄)
row = 4, col = 0에서 떨어진게 없으므로 0
row = 4, col = 1에서 0.3125떨어졌으므로 0.3125
row = 4, col = 2에서 0.3125가 2번 떨어졌으므로 0.625
row = 4, col = 3에서 0.3125떨어졌으므로 0.3125
row = 4, col = 4에서 떨어진게 없으므로 0
이것을 코드로 나타내면 다음과 같다.
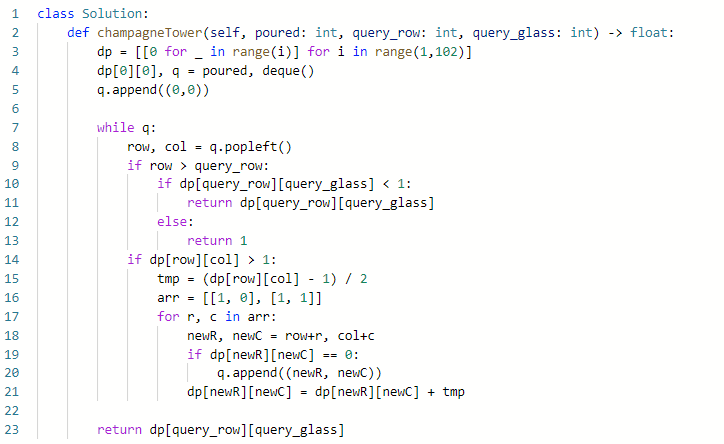
즉 큐에 (0,0) => poured값을 넣고 dp[row][col] > 1보다 크다는 것은 떨어질 수 있는 양이 있다는 의미이므로 양 옆((row + 1, col), (row + 1, col + 1))에 떨어지는 양을 더한다.
그리고 한번도 저장된 적이 없다면 q에 넣어주고 계속해서 1보다 작아질 때까지 탐색한다. 그러다가 원하는 query_row, query_glass를 찾기 위해서 다음과 같은 조건을 명시하여 리턴해준다.
결과(BFS)