935. Knight Dialer
https://leetcode.com/problems/knight-dialer/
문제
풀이(처음 풀었던 답 TLE)
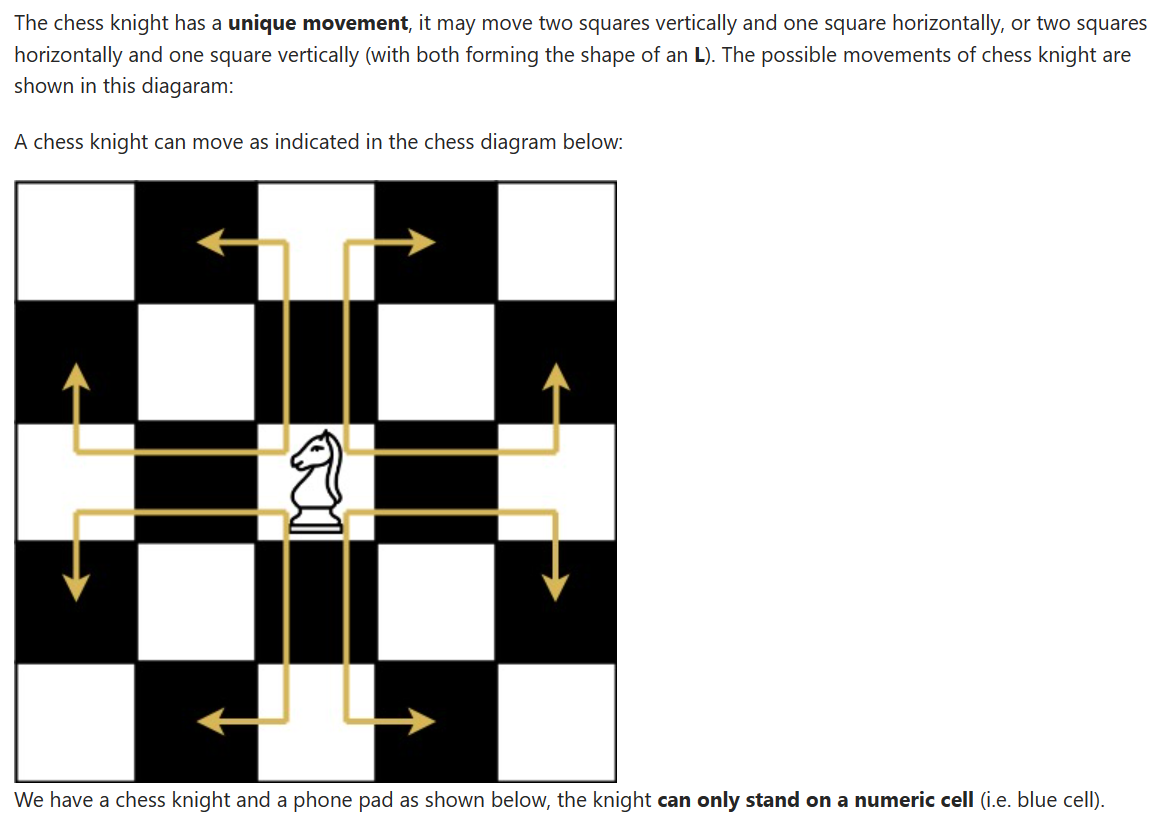
나이트가 움직일 수 있는 경로는 8가지 이다.
움직일 수 있는 경로를 배열로 나타내면 다음과 같다.
arr = [[1, 2], [2, 1], [2, -1], [1, -2], [-1, -2], [-2, -1], [-2, 1], [-1, 2]] => [row, col]기준
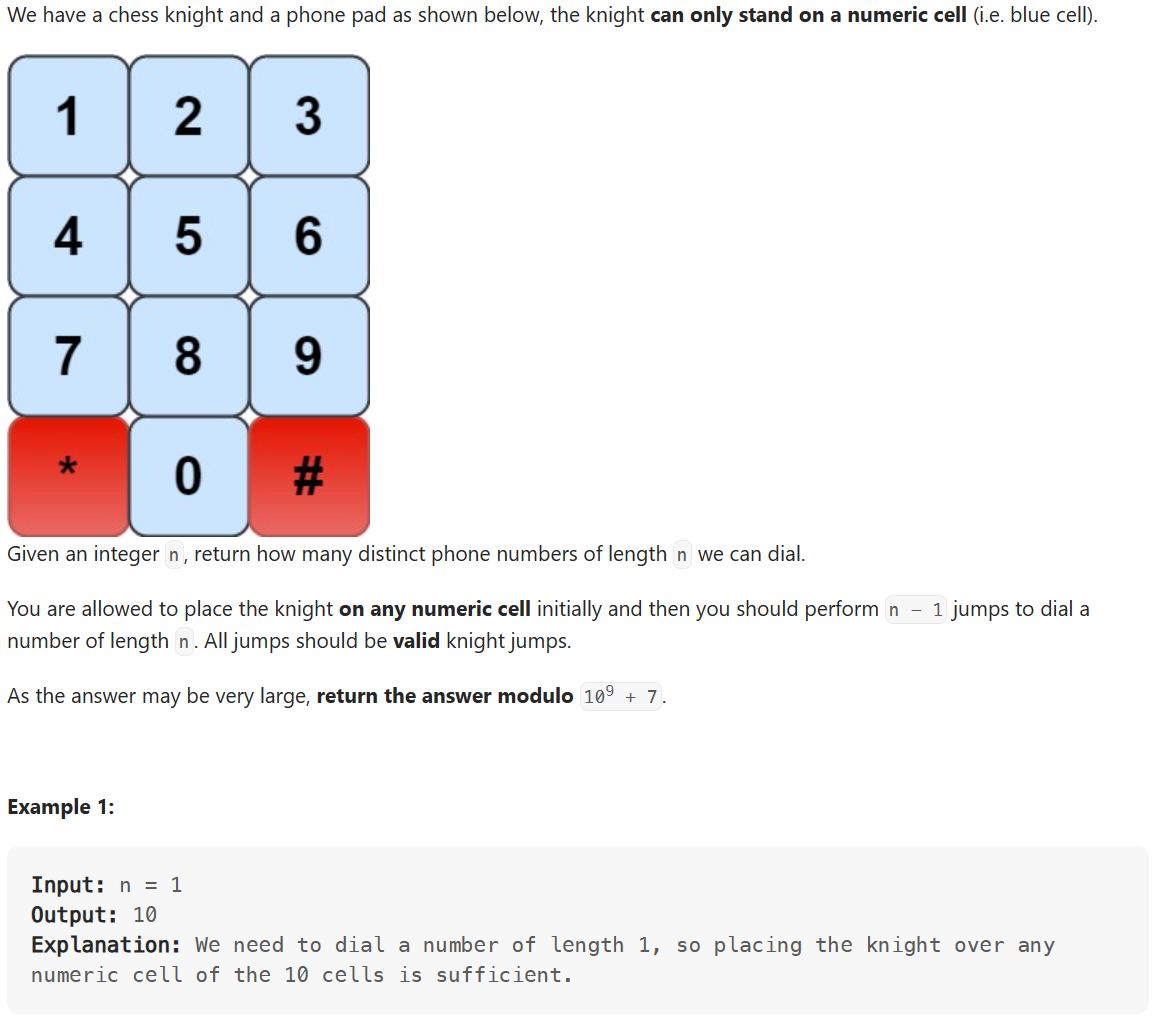
또한 문제에서 제시한 다이얼을 2차원배열로 나타내면 다음과 같다.
dial = [[1,2,3], [4,5,6], [7,8,9],[-1,0,-1]] => *, #은 -1로 표현
즉 나이트가 8가지 경로중에서 dial 위에 있다면 또 다음 탐색을 진행하고 dial위에 없다면 0을 리턴하였다.
이것을 토대로 코드로 나타내면 다음과 같다.

dial 위에 없다는 조건은 코드 10번째 줄에 작성하였고 문제에서 *,#에서 움직이지 못한다고 했으므로 이 조건을 추가하였다. 그래서 depth가 n만큼 되었을 때 1을 리턴하면 최종 총 개수를 얻을 수 있게 된다.

하지만 TLE라는 결과가 나왔다. 찾아본 결과 arr이 배열 때문이였다. 그 이유는 dfs 함수 재귀호출할 때 arr를 새 복사본으로 다시 만들기 때문이다. 이것을 전역변수로 빼주었더니 통과하였다.
풀이(두 번째 풀이 - DFS)

처음 풀었던 풀이와 바뀐 것은 arr위치이다. arr를 전역변수에 위치해 두고 참조하는 식으로 변경하였더니 통과하였다.
하지만 많이 느렸고 더 최적화 할 수 있는 방법이 있는지 찾아보았다.
풀이(세 번째 풀이 - DFS)
앞서서 풀었던 풀이는 나이트가 이동할 수 있는 경로 8가지를 arr에 저장하고 8가지 경로를 일일이 확인하여 다이얼 위에 있는지 없는지 확인하였다. 하지만 나이트가 갈 수 있는 경로는 정해져있다.
adj = {
1: (6, 8),
2: (9, 7),
3: (4, 8),
4: (0, 3, 9),
5: (),
6: (0, 1, 7),
7: (2, 6),
8: (1, 3),
9: (2, 4),
0: (4, 6)
} 즉 다이얼 1에 있을 때 갈 수 있는 경로는 6, 8이고
다이얼 5에 있을 때 갈 수 있는 경로는 없다.
다이얼 0에 있을 때 갈 수 있는 경로는 4, 6이다. 이것을 적용한다면 일일이 8가지 경로를 탐색할 필요가 없고 adj에 경로만 탐색하면 되는 것이다. 이것을 코드로 적용하면 다음과 같다.
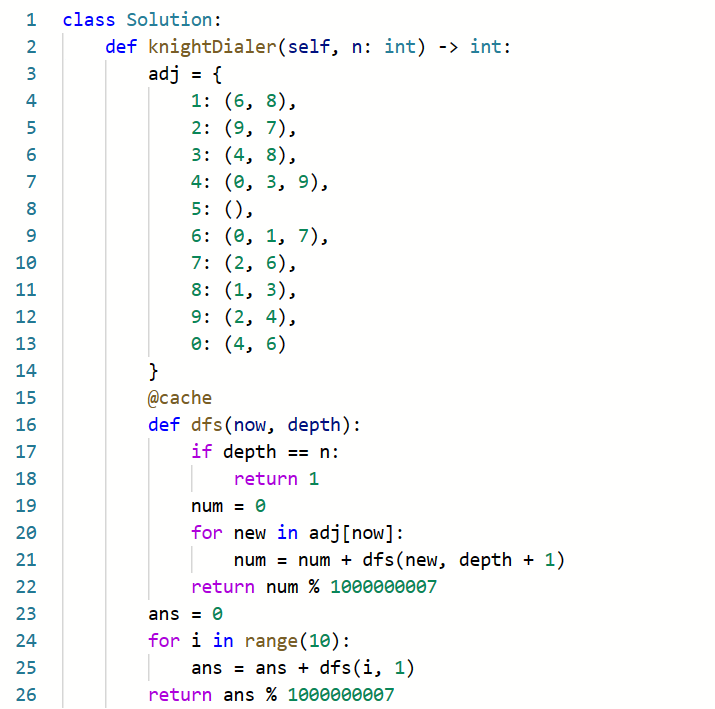
전보다 확연히 빨리졌다.
