Non-overlapping Intervals
https://leetcode.com/problems/non-overlapping-intervals/
문제
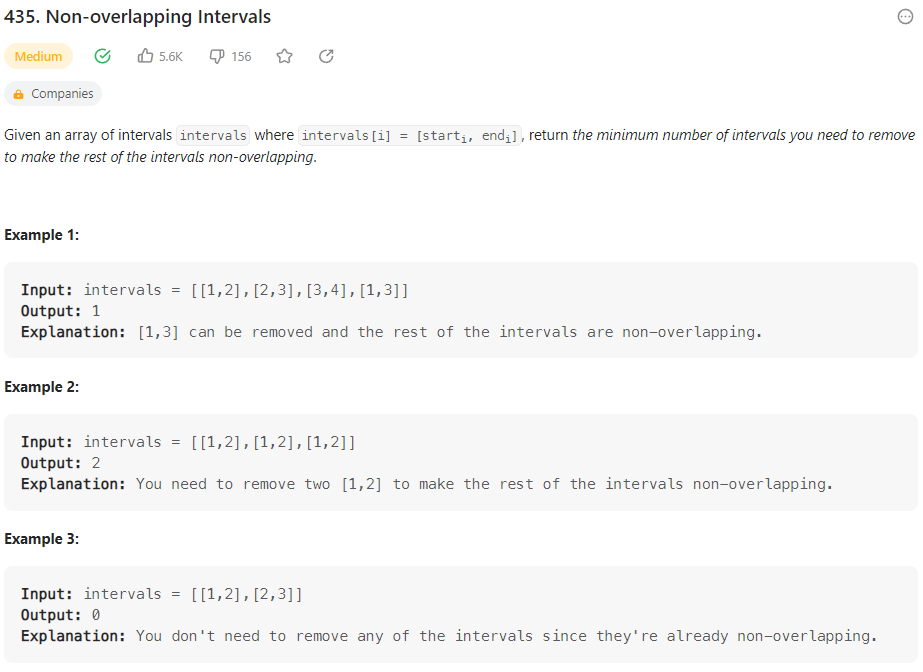
풀이(처음 풀었던 답 - TLE)
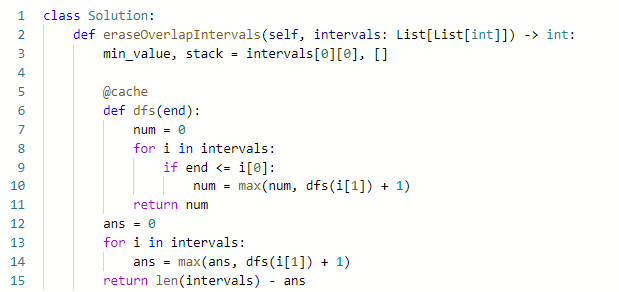
모든 경우의 수를 탐색한다. Example 1을 기준으로 설명하자면
[1, 2]를 먼저 시작하면 다음 올 수 있는 것은 2이상이어야 한다.
2 이상인 경우는 [2, 3], [3, 4]뿐이고 [1, 3]은 2보다 작기 때문에 되지 않는다.
즉 [1, 2][2, 3] 또는 [1, 2][3, 4]가 될 수 있는데 [1, 2][2, 3]일 때 3보다 큰 값은 [3, 4]뿐이다. 즉 [1, 2][2, 3][3, 4]가 되고
[1, 2][3, 4]일 때 4보다 큰 값은 없으므로 [1, 2][3, 4]가 된다.
즉 [1, 2]로 시작할 때 겹치지 않는 최대값은 3이 된다. 이렇게 [1, 2]로 시작할 때뿐만아니라 intervals에 있는 모든 숫자를 탐색해 최대값을 구한다음 그 중에서 최대값을 구한다.
이렇게 하면 시간 복잡도 측면에서 최소 n^2이상일 것이다.
풀이(두 번째 풀었던 답 - TLE)

처음 풀었던 답에서는
[1, 2]에서 가능한 모든 경우의 수 [2, 3], [3, 4]를 탐색하는 것이 아니라 [2, 3], [3, 4]중에서 end값이 최소인 값을 탐색하는 것이다. 즉 [2, 3], [3, 4]에서 3이 4보다 작으므로 [2, 3]을 탐색하는 것이다. 이렇게 하면 시간복잡도 측면에서 n^2이 되지만 n이 클 수록 좋지 않다.
풀이(세 번째 풀었던 답 - 투 포인터)
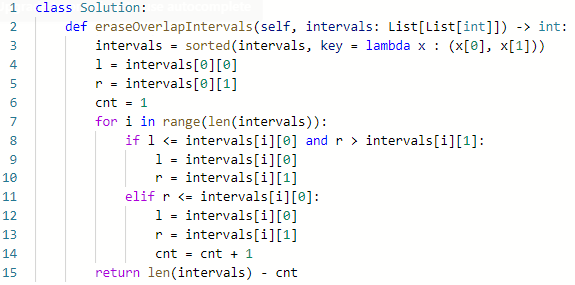
intervals = [[1, 2], [2, 6], [3, 5], [6, 7]]이라 하자
초기값으로 l = 1, r = 2로 초기화 한다.
i = 1일 때 [2, 6]이므로 겹치지지 않는다. 따라서 포인터를 옮긴다.
l = 2, r = 6, cnt = 2가 된다.
i = 2일 때 [3, 5]이므로 겹치진다. 이제 어떤 것이 더 나은 값인지 알아야 하는데 기존에는 6이지만 현재는 5이기 때문에 더 작은 값으로 갱신한다.
l = 3, r = 5, cnt = 2가 된다.
i = 3일 때 [6, 7]이므로 겹치지지 않는다.
cnt = 3
이렇게 전체길이와 최대로 연결될 수 있는 개수를 빼게 되면 원하는 값을 얻을 수 있다.
풀이(세 번째 풀었던 답 - 투 포인터)