Database 저장
- database 저장 장치
- 데이터 저장하는 방법, 접근에 영향
- 직접 접근 저장 장치 (DASD)인 disk 사용 (Nonvolatile storage, Online device)
- 임의 접근 시간
- 데이터 접근 시간
- 헤드가 원하는 트랙에 있는 레코드 찾아 전송하는데 걸리는 시간
- 탐구시간 + 회전지연시간 + 데이터 전송 시간
- 접근 시간은 메인 메모리 접근 시간에 비해 느림
- 실제 데이터 전송 시간은 전체의 10분의 1!!!
- 대량 전송률 : 연속적인 블록 전송하는 시간
- database 성능 향상 초점 : 디스크 접근 횟수 최소화!!!
(디스크에 배치, 저장하는 방법이 중요한 문제)
Database 접근
- Database 접근 과정
- DBMS는 사용자가 요구하는 레코드 결정 (file manager에게 그 저장 레코드 검색 요청)
- file manager는 저장 레코드가 들어있는 페이지 결정 (disk manager에게 그 페이지 검색 요청)
- disk manager는 그 페이지의 물리적 위치를 결정 (디스크에 I/O 명령 내림)
디스크 관리자
-
기본 입출력 서비스 지원 모듈
- 모든 물리적 I/O 연산에 대한 책임
- 물리적 디스크 주소 알고 있음
- operating system의 한 구성 요소
-
file manager를 지원
- file manager가 디스크를 일정 크기의 페이지, 즉 블록으로 구성된 page set로 취급할 수 있도록 지원
- page set 중에는 하나의 free space page set가 있음
- 각 page는 해당 디스크 내에서 유일한 page number 가짐
-
디스크 관리
- 페이지 번호를 물리적 디스크 주소로 mapping
-> file manager를 장비에서 독립 - file manager의 요청에 따라 page set에 대한 페이지 할당, 회수 수행
- 페이지 번호를 물리적 디스크 주소로 mapping
-
disk manager의 페이지 관리 연산
- file manager가 명령 가능한 연산
- page set S로부터 페이지 P의 검색
- S 내에서 P의 교체
- S에 새로운 P 첨가
- S에서 P 제거
-> 3, 4는 자유 공간 다룸 & disk manager 필요에 따른 연산임
- file manager가 명령 가능한 연산
파일 관리자
- DBMS가 디스크 저장 공간을 저장 화일들의 집합으로 취급할 수 있도록 지원
- 저장 화일
- 한 타입의 저장 레코드 어커런스들의 집합
- 한 page set는 하나 이상의 저장 화일을 저장
- 화일 이름 또는 화일 ID로 식별
- 저장 레코드
- 레코드 번호 또는 레코드 ID로 유일하게 식별
- 전체 디스크 내에서 유일
- <페이지 번호, 오프셋(슬롯 번호)>
- file manager의 화일 관리 연산
- DBMS가 file manager에게 명령 가능한 연산
- 저장 화일 f에서 저장 레코드 r을 검색
- f에 있는 저장 레코드 r을 대체
- f에 새로운 레코드 첨가하고 새로운 레코드 ID, r을 반환
- f에서 저장 레코드 r을 제거
- 새로운 저장 화일 f를 생성
- 저장 화일 f를 제거
- DBMS가 file manager에게 명령 가능한 연산
Page Set과 화일
- disk manager의 페이지 관리
: file manager가 물리적 디스크 I/O가 아닌 논리적인 페이지 I/O를 수행할 수 있게끔 지원하는 disk manager의 기능 - 대학 데이터베이스 예
- 레코드들의 논리적 순서는 그림과 같이 학번, 과목번호, 학번-과목번호 순
- 저장 순서도 논리적 순서와 같다
- 저장 화일들은 28개의 페이지로 구성된 page set에 저장
- 각 레코드들은 하나의 페이지를 차지
대학 데이터베이스 예제 연산 과정
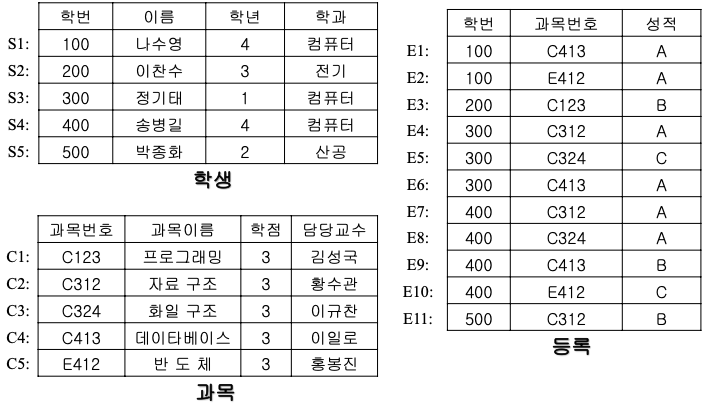
- 빈 디스크 :
하나의 자유 공간 page set만 존재(1~27)
페이지 0 제외 : 디렉터리 - file manager : 5개의 학생 화일 레코드를 삽입
- disk manager : 자유 공간 page set의 페이지 1에서 5까지를 학생 page set이라 이름 붙이고 할당
- 과목과 등록 화일에 대한 page set를 할당
- 4개의 page set가 만들어짐
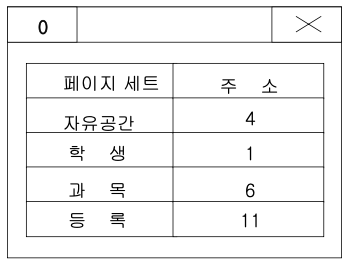
- 학생(1~5), 과목(6~10), 등록(11~21), 자유공간 page set(22~27)
대학 데이터베이스의 초기 적재 후 디스크 배치도
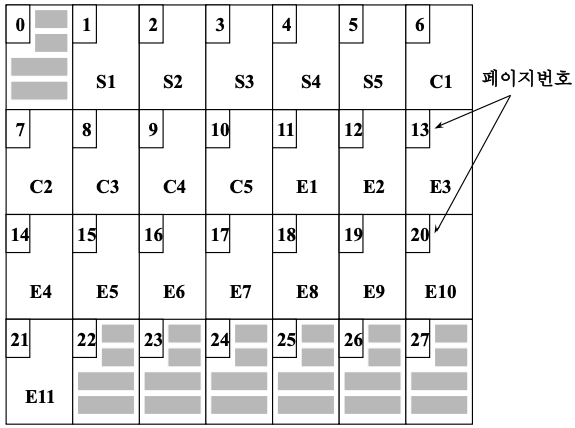
- 연산 과정
- file manager : 새로운 학생 S6 (학번 600)을 삽입
disk manager : 첫번째 자유 페이지(페이지22)를 자유 공간 page set에서 찾아서 학생 page set에 첨가 - file manager : 학생 S2 (학번 200)을 삭제
disk manager : S2가 저장되어 있던 페이지 (페이지 2)를 자유 공간 page set으로 반납 - file manager : 새로운 과목 C6 (E 515)를 삽입
disk manager : 자유 공간 page set에서 첫 번째 자유 페이지 (페이지 2)를 찾아서 과목 page set에 첨가 - file manager : 학생 S4를 삭제
disk manager : S4가 저장되어 있던 페이지 (페이지 4)를 자유 공간 page set에 반납
- file manager : 새로운 학생 S6 (학번 600)을 삽입
삽입, 삭제 연산 뒤의 디스크 배치도
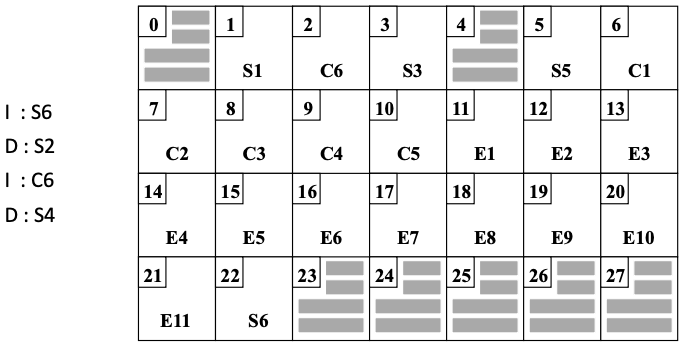
- 일련의 삽입, 삭제 뒤에는 page set들의 물리적 인접성이 없어짐
Pointer 표현 방법
- 한 page set에서 페이지의 논리적 순서를 물리적 인접으로 표현하기 어려움
- 페이지 헤드에 제어 정보를 저장
- next page pointer
: 논리적 순서에 따른 next page의 물리적 주소, next page pointer는 disk manager가 관리 (file manager는 무관)
- next page pointer
- 페이지 헤드에 next page pointer가 포함되어 있는 경우의 디스크 배치도
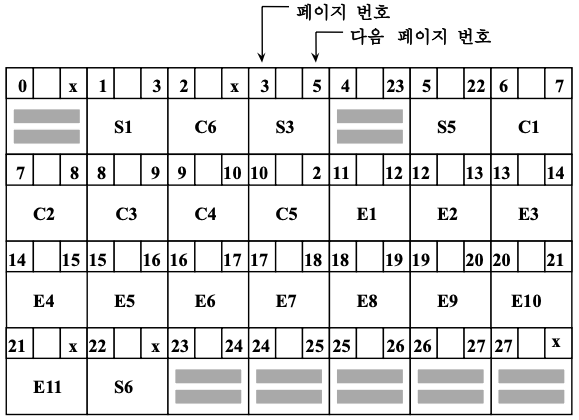
- disk directory (page set 디렉터리)
- 실린더 0, 트랙 0에 위치
- 디스크에 있는 모든 page set의 리스트와 각 page set의 첫 번째 페이지에 대한 포인터를 저장
- disk directory (페이지 0)
파일 관리자의 기능
-
저장 레코드 관리
: DBMS가 페이지 I/O에 대해 알 필요 없이 저장 화일과 저장 레코드로 처리할 수 있도록 지원 -
예시
- 하나의 페이지에 여러 개의 레코드 저장
- 학생 레코드에 대한 논리적 순서는 학번 순
-
페이지 p에 5개의 학생 레코드(S1 ~ S5)가 삽입 되었다고 가정
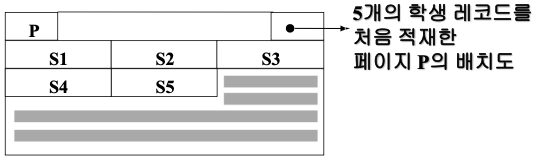
-
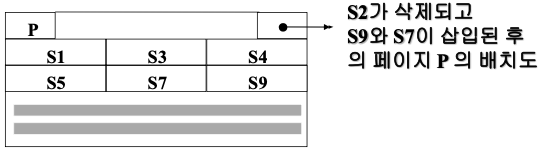
DBMS : 학생 레코드 S9 (학번 900)의 삽입 요청
-> 페이지 p의 학생 레코드 S5 바로 다음에 저장 -
DBMS : 레코드 S2의 삭제 요청
-> 페이지 p에 있는 학생 레코드 S2를 삭제하고 뒤에 있는 레코드들을 모두 앞으로 당김 -
DBMS : 레코드 S7 (학번 700)의 삽입 요청
-> 학생 레코드 S5 다음에 들어가야 하므로 학생 레코드 S9를 뒤로 옮김
RID의 구현
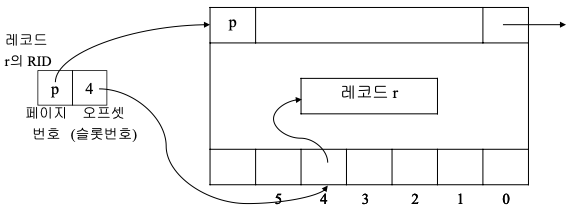
- RID = <페이지 번호 p, 오프셋(슬롯번호)>
- 오프셋 내용 = 페이지 시작에서부터 저장된 레코드의 위치를 저장
- 레코드 위치 변경 시 RID의 변경 없이 오프셋의 내용만 변경
- 최악의 경우 두 번의 접근으로 원하는 레코드 검색 가능
- 해당 페이지가 overflow 되어 다른 페이지로 저장된 경우 두 번 접근
Note!
- 화일에 있는 모든 저장 레코드들의 순차적 접근
- 순차적 접근 : page set 내에서는 페이지 순서, 페이지 내에서는 레코드 순서
- 레코드 순서 : RID의 오름차순
- control information
- 저장 레코드에 있는 정보 중, 시스템이 필요로 하는 정보
- file ID
- record length
- deletion flag
- 레코드 앞에 prefix로 만들어 저장
- 일반 사용자에게는 무관
- 저장 레코드에 있는 정보 중, 시스템이 필요로 하는 정보
- user 데이터 필드
- 저장 레코드에 있는 정보 중, 사용자가 필요로 하는 정보
- DBMS가 이용, file manager와 disk manager는 알 필요 없음
(화일 관리자는 화일을 단순히 바이트 스트링으로 인식)
File의 조작 방법
- 파일 : DBMS에서 관리하는 모든 데이터는 파일 형태로 기록 (같은 타입의 레코드들의 집합)
- 레코드의 저장과 접근 방법을 결정
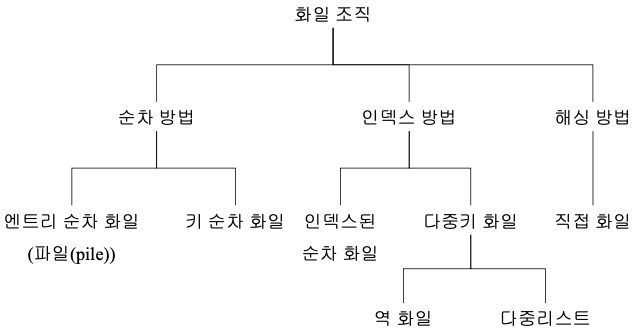
순차 방법
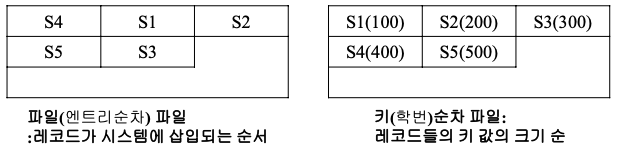
- 레코드들의 논리적 순서가 저장 순서와 동일
- heap 또는 파일 : 엔트리 순차 화일
- 일반적인 순차 화일 : 키 순차 화일
- 레코드 접근 - 물리적 순서
- 화일 복사, 순차적 일괄 처리 응용
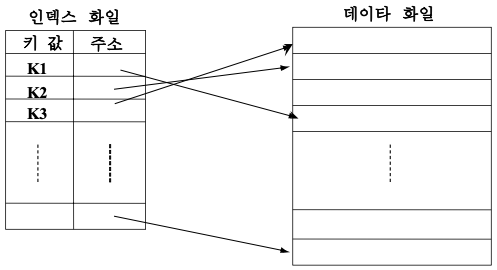
인덱스 방법
- 인덱스를 통해 데이터 레코드를 접근
- 인덱스된 파일의 구성
- 인덱스 파일
- 데이터 화일
인덱스 된 순차 파일
- 하나의 인덱스를 사용
- 순차 접근과 직접 접근을 지원
- 순차 데이터 화일
- 레코드를 순차적으로 정렬 -> 레코드 집합 전체에 대한 순차 접근 요구를 지원하는데 사용
- 순차 접근 방법
- 인덱스
- 레코드들에 대한 포인터 -> 개별 레코드들에 대한 임의 접근 요구를 지원하는데 사용
- 직접 접근 방법
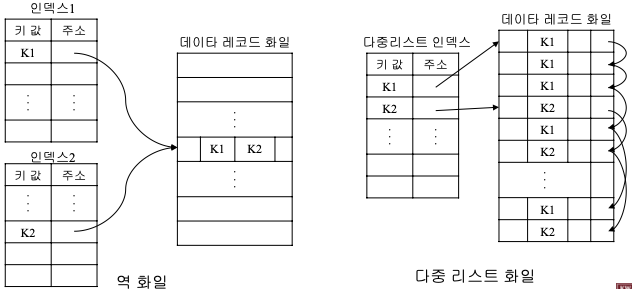
다중 키 파일
- 데이터를 중복시키지 않으면서 여러 방법으로 데이터를 접근할 수 있는 경로를 제공
- 역 화일 -> 각 응용에 적합한 인덱스를 선정해 구축
- 다중 리스트 화일 -> 하나의 인덱스 값마다 데이터 레코드 리스트를 구축
Index 종류
- 인덱스의 구조
- <레코드 키 값, 포인터(레코드 주소)>
- 레코드 키 값은 탐색 키 값임
- 기본 인덱스
- 기본 키를 포함한 인덱스
- 하나의 레코드만 식별
- 보조 인덱스
- 보조 키를 포함
- 여러 개의 레코드를 식별
- 집중 인덱스
- 탐색 키 값 순서와 데이터 레코드의 물리적 순서가 같도록 구성된 인덱스 -> 기본 인덱스는 집중 인덱스의 특수한 경우
- 화일에 하나만 존재 가능
- 동일한 탐색 키 값을 가진 레코드는 물리적으로 집단화 되어 검색이 효율적
- 비 집중 인덱스
- 집중 인덱스가 아닌 인덱스
- 하나의 데이터 화일에 여러 개 존재 가능
- 밀집 인덱스
- 모든 탐색 키 값에 대해 하나의 인덱스 엔트리가 만들어진 인덱스
- 역 인덱스는 보통 밀집 인덱스 형태
- 희소 인덱스
- 일부 탐색 키 값에 대해 인덱스 엔트리가 만들어진 인덱스
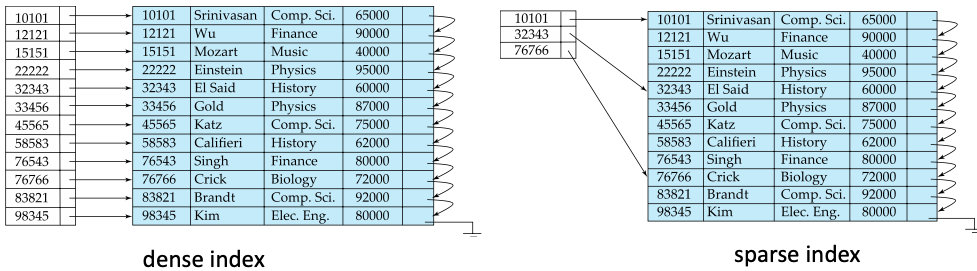
- 일부 탐색 키 값에 대해 인덱스 엔트리가 만들어진 인덱스
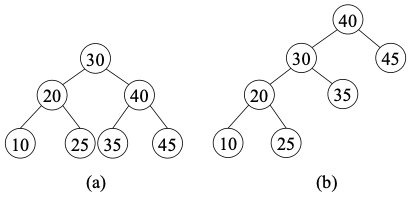
이진 검색 트리
- 이진검색트리의 각 노드는 키 값을 하나씩 가짐.
- 최상위 레벨에 루트 노드가 있고, 각 노드는 최대 두 개의 자식 가짐
- 임의의 노드 키 값은 자신의 왼쪽 자식 노드의 키 값보다 크고, 오른쪽 자식의 키 값보다 작다.
B-트리
- 디스크의 접근 단위는 블록
- 디스크에 한 번 접근하는 시간은 수십만 명령어의 처리 시간과 맞먹는다
- 검색 트리가 디스크에 저장되어 있다면 트리의 높이를 최소화 하는 것이 유리
- B-트리는 다진검색트리가 균형 유지하도록 하여 최악의 경우 디스크 접근 횟수를 줄인 것임
- B-트리는 균형잡힌 다진검색트리로 다음의 성질을 만족
- 루트 제외한 모든 노드는 적어도 [m/2]-1 개의 키 값 (최대 m개의 서브 트리)를 갖는다
- 모든 리프 노드는 같은 깊이 가짐
- B-트리의 노드 구조
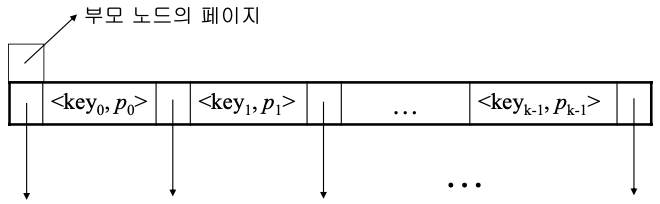
다진 검색 트리
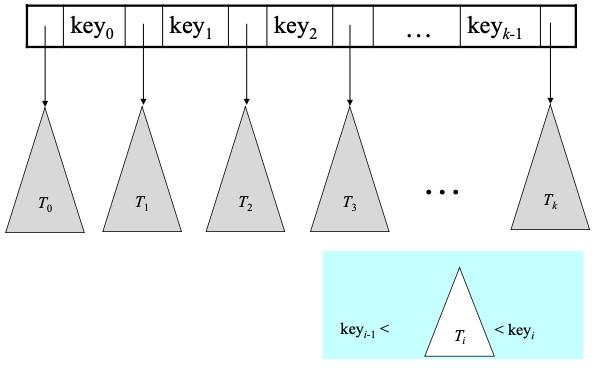
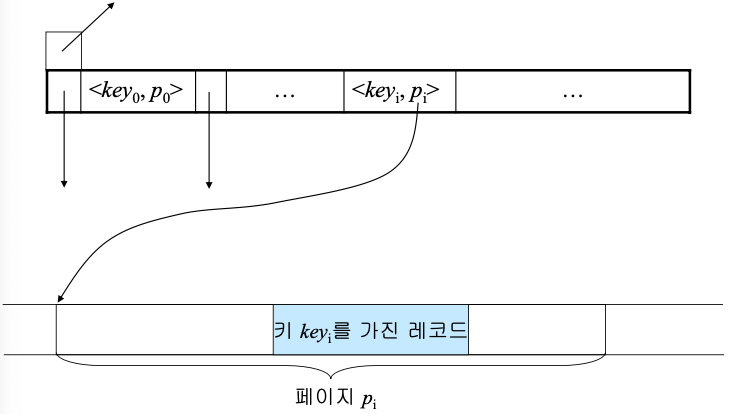
레코드 접근
- B-트리를 통해 레코드에 접근하는 과정
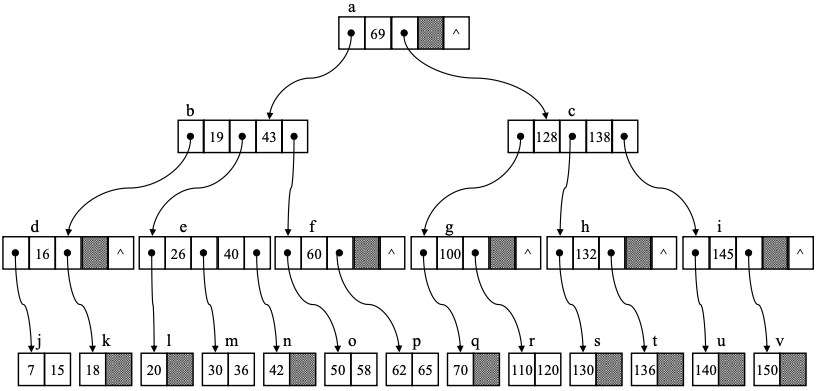
3차 B-트리
연산
- B-트리에서의 연산
- 직접 탐색 : 키 값에 의한 분기
- 순차 탐색 : 중위 순회로 가능
- 삽입, 삭제 : 연산 뒤에 트리의 균형을 유지해야됨
- 분할 : 노드의 오버플로 발생 시
- 합병 : 노드의 언더플로 발생 시
- 삽입
- 삽입은 항상 리프 노드에서 수행하게 됨
- 빈 공간 있는 경우 : 단순히 빈 공간에 삽입하면 됨
- 오버플로
1) 두 노드로 분할
2) [m/2] 번째의 키 값 -> 부모 노드에 삽입
3) 나머지는 반씩 왼쪽, 오른쪽 서브트리가 됨
- 삽입은 항상 리프 노드에서 수행하게 됨
삽입 알고리즘
BTreeInsert(t,x)
{
x를 삽입할 리프 노드 r을 찾는다;
x를 r에 삽입한다;
if (r에 오버플로우 발생) then clearOverflow(r);
}
clearOverflow(r)
{
if (r의 형제 노드 중 여유가 있는 노드가 있음) then {
r의 남는 키를 넘긴다};
else {
r을 둘로 분할하고 가운데 키를 부모 노드로 넘긴다;
if (부모 노드 p에 오버플로우 발생) then clearOverflow(p);삽입 예
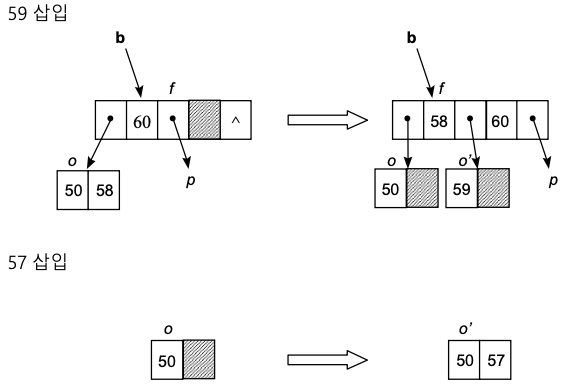
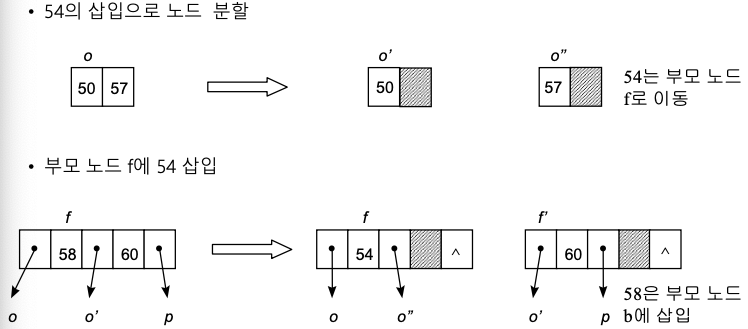
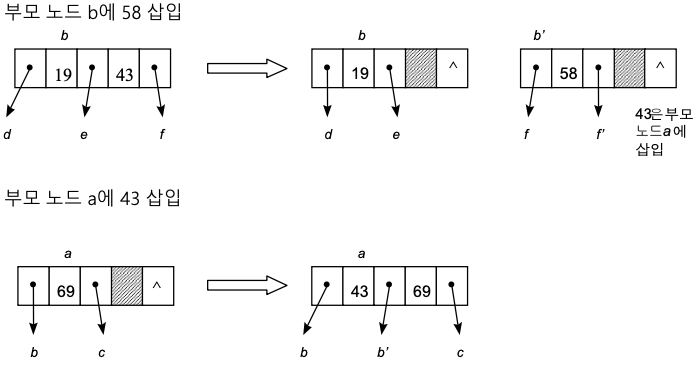
연산
- 삭제
- 리프 노드에서는 그대로 삭제
- 삭제할 키가 리프가 아닌 노드에 존재하는 경우
- 후행 키 값과 자리 교환을 하고 리프 노드에서 삭제
- 키 값의 수 < [m/2]-1이 되어 언더플로가 발생
- 재분배 : [m/2] 개 이상의 키를 가지고 있는 형제 노드가 있는 경우에 그 형제 노드로부터 키를 이동
- 합병 : 재분배 불가능 시 (형제 노드 + 부모 노드의 키 + 언더플로 노드)
삭제
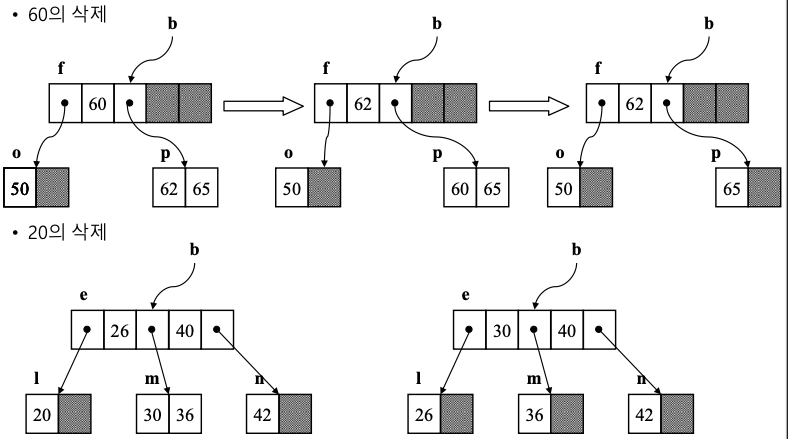
B+-트리
-
B+- 트리는 인덱스 세트와 순차 세트로 구성
- 인덱스 세트
- 내부 노드로 구성되고 리프 노드에 있는 키들에 대한 경로만 제공
- 직접 접근을 지원
- 순차 세트
- 리프 노드로 구성되고 모든 키 값들을 저장
- 순차 세트는 순차적으로 연결
-> 순차 접근을 지원 - 리프 노드는 내부 노드와 상이한 구조를 가짐
-
m차 B+-트리의 특성
- 노드 구조는 <n, P0, K1, - - ,P n-1 Kn, Pn>
- n : 키 값의 수
- P0, - - , Pn : 서브트리에 대한 포인터
- K1, - - , Kn : 키 값
- 루트는 0이거나 2에서 m개 사이의 서브트리를 가짐
- 리프가 아닌 노드에 있는 키 값의 수는 그 노드의 서브트리 수보다 하나 적음
- 모든 리프 노드는 같은 레벨
- 한 노드 안에 있는 키 값들은 오름차순
- 노드 구조는 <n, P0, K1, - - ,P n-1 Kn, Pn>
-
Pi가 지시하는 서브트리에 있는 노드들의 모든 키 값들은 K i+1보다 작거나 같음
-
Pn이 지시하는 서브트리에 있는 노드들의 모든 키 값들을 Kn보다 크다
-
순차 세트를 구성하는 리프 노드는 모두 링크로 연결된 연결 리스트를 구성
-
리프 노드 구조
<q, <K1, A1>, <K2, A2>, -- <Kq, Aq>, P next>- Ai : 키 값 Ki를 가지고 있는 레코드에 대한 주소
- q : [m/2]<=q
- P next : 다음 리프 노드에 대한 링크
-
B-트리와의 차이점
- 인덱스 세트에 있는 키 값을 찾아가는 경로로만 제공하기 위해 사용
-> 인덱스 세트에 있는 키 값은 모두 순차 세트에 다시 나타남 - 인덱스 세트의 노드와 순차 세트의 노드는 그 내부 구조가 서로 다름
- 리프 노드 : 키 값과 이 키 값을 가진 레코드에 대한 주소가 함께 저장
- 인덱스 세트 노드 : 키 값만 저장
- 노드에 저장할 수 있는 원소의 수도 서로 다름
- 순차 세트의 모든 노드가 순차적으로 연결된 연결 리스트
- 순차 접근을 효율적으로 지원
- 인덱스 세트에 있는 키 값을 찾아가는 경로로만 제공하기 위해 사용
차수가 3인 B+-트리
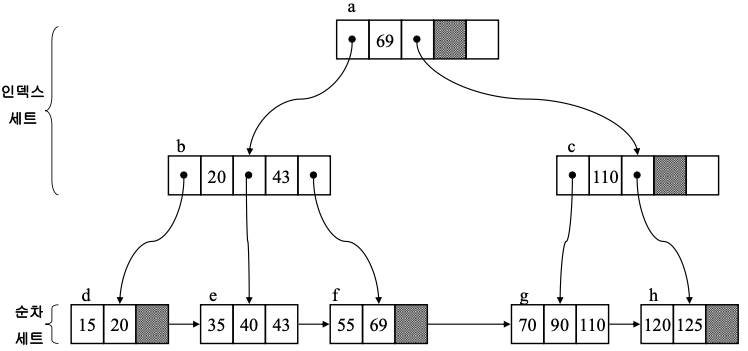
B+-트리의 연산
- 탐색
- B+-트리의 인덱스 세트 : m-원 탐색 트리와 같음
- 레코드는 리프에서 검색
- 삽입
- B-트리와 유사
- 리프가 오버플로가 되면 분할 -> 중간 키 값은 부모 노드로 올라가 저장되지만 분할 노드에도 존재
- 순차 세트의 연결 리스트의 순차성 유지
- 삭제
- 리프에서만 삭제 (재분배, 합병이 필요 없는 경우)
- 인덱스 세트에 있는 키 값은 분리자로 유지 (키 값 탐색하는데 분리 키 값으로 사용)
- 재분배 : 인덱스 키 값 변화, 트리 구조 유지
- 합병 : 인덱스의 키 값도 삭제
- 삭제 예
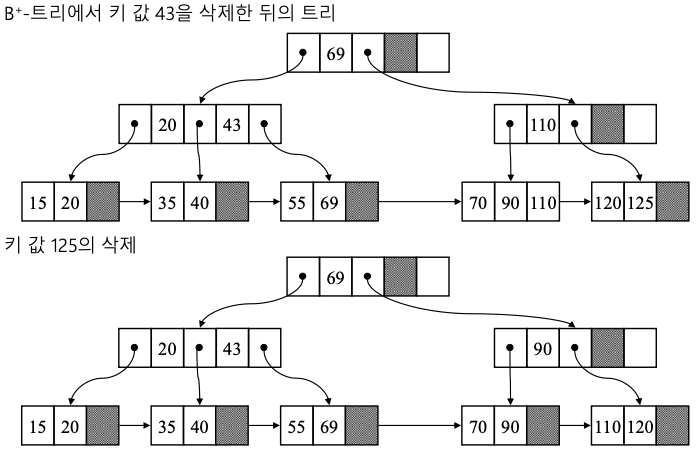
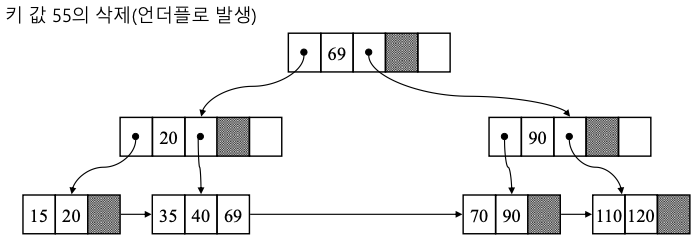
- 리프에서만 삭제 (재분배, 합병이 필요 없는 경우)
해싱 방법
- 다른 레코드의 참조 없이 목표 레코드의 접근을 직접 지원 - 직접 화일
- 키 값과 레코드 주소 사이의 mapping 관계를 함수로 설정
- 해싱 함수
- 키 값으로부터 레코드 주소를 계산
- 사상 함수 : 키 -> 주소
- 삽입, 검색에 모두 이용
버킷 해싱
- 버킷
- 하나의 주소를 가지면서 하나 이상의 레코드를 저장할 수 있는 화일의 한 구역
- 버킷 크기 : 저장 장치의 물리적 특성과 한번 접근으로 채취 가능한 레코드 수를 고려
- 버킷 해싱 : 키 -> 버킷 주소
- 충돌 : 상이한 레코드들을 같은 주소로 변환
- 동거자
- 버킷 만원 - 오버플로 버킷
- 한번의 I/O가 추가됨
충돌 해결
- 체이닝
- 같은 주소로 해싱되는 원소를 모두 하나의 연결 리스트로 관리
- 추가적인 연결 리스트 필요
- 개방주소 방법
- 충돌 일어나도 어떻게든 주어진 테이블 공간에서 해결
- 추가적인 공간 필요하지 않음
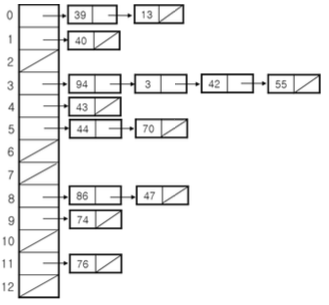
- 빈자리가 생길 때까지 해시값 계속 만들어낸다
- 중요한 세가지 방법 : 선형 조사, 이차원 조사, 더블 해싱
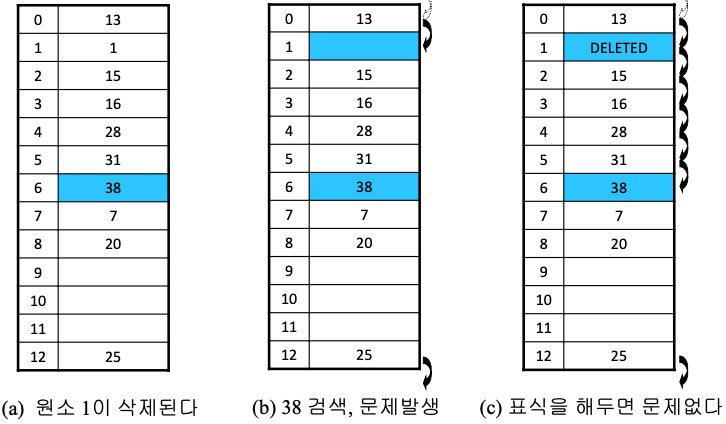
충돌 해결 : 선형 조사
hi (x) = (h(x) + i) mod m
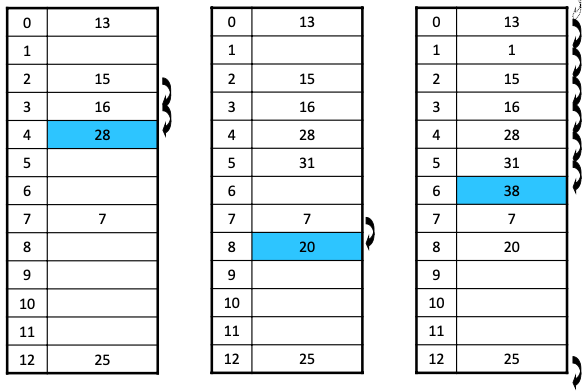
- 선형 조사
: 1차 군집에 취약함 (1차군집 : 특정 영역에 원소 몰리는 현상)
충돌 해결 : 이차원 조사
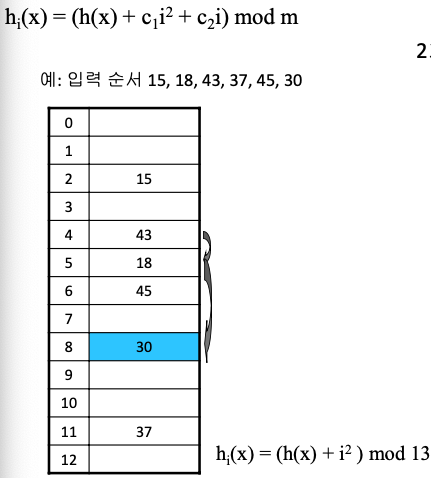
- 2차군집 : 여러 개의 원소가 동일한 초기 해시 함수값을 갖는 현상
충돌 해결 : 더블 해싱

- 충돌 해결 : 개방 주소 방법 시 주의할 점
확장성 해싱
- 충돌에 대처하기 위해 제안된 기법
- 레코드 검색은 최대 2번의 디스크 접근만 필요
- 모조 키
- 확장성 해싱 함수 : 키 값 -> 일정 길이의 비트 스트링, pseudokey로 변환
- pseudokey의 처음 d 비트를 디렉터리의 인덱스로 사용
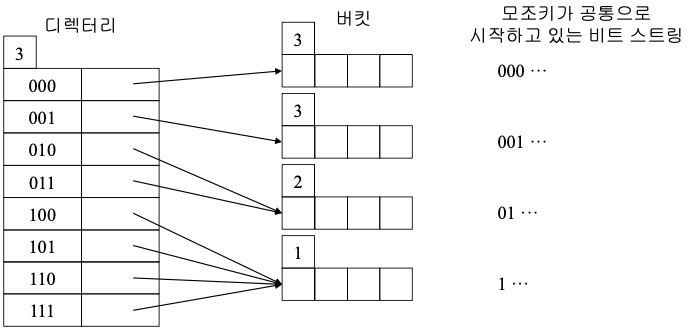
- 디렉터리
- 헤더에 현재의 디렉터리 깊이 d를 유지
d : 전역 깊이 - 2^d개의 버킷들을 지시할 수 있는 포인터 엔트리로 구성
- 디스크에 저장
- 헤더에 현재의 디렉터리 깊이 d를 유지
- 버킷
- 헤더에 현재의 버킷 깊이 p를 유지, p = 지역 깊이
- 각 버킷에 저장된 레코드들의 모조 키들은 처음 p비트가 모두 동일
확장성 해싱의 연산
- 검색
- 모조 키의 처음 d 비트를 디렉터리에 대한 인덱스로 사용
- 접근된 디렉터리 엔트리는 목표 버킷에 대한 포인터 제공
- 검색 예
1) 레코드 키 값 k -> 모조키 101000010001
2) 디렉터리 깊이가 3이므로 모조 키의 처음 3비트 사용- 디렉터리의 6번째 (101) 엔트리 접근
3) 엔트리는 4번째 버킷에 대한 포인터 - 키 값 k를 가지고 있는 레코드가 저장되어있는 버킷
- 버킷 깊이, p=1 : 모조 키의 공통 비트 수가 1, 즉 이 버킷은 비트 1로 시작하는 레코드들을 저장
- 디렉터리의 6번째 (101) 엔트리 접근
- 저장
- 저장할 레코드 모조 키의 처음 d 비트로 디렉터리 접근
- 엔트리 포인터가 지시하는 버킷에 레코드 저장
- 버킷의 오버플로 처리
- 새로운 버킷 할당
- 버킷 깊이가 p인 오버플로된 버킷과 새로 할당된 버킷의 깊이를 모두 p+1로 설정
- 오버플로된 버킷에 있는 레코드들과 새로 저장할 레코드를 모조키의 p+1 번째 값에 따라 기존의 오버플로된 버킷과 새로 할당한 버킷에 분산
- 이때 d < (p+1) 되면 디렉터리 오버플로가 발생
-> d값을 1 증가시켜 디렉터리 크기를 2배로 확장
-> 2배로 증가된 디렉터리 엔트리 포인터들을 모두 조정
