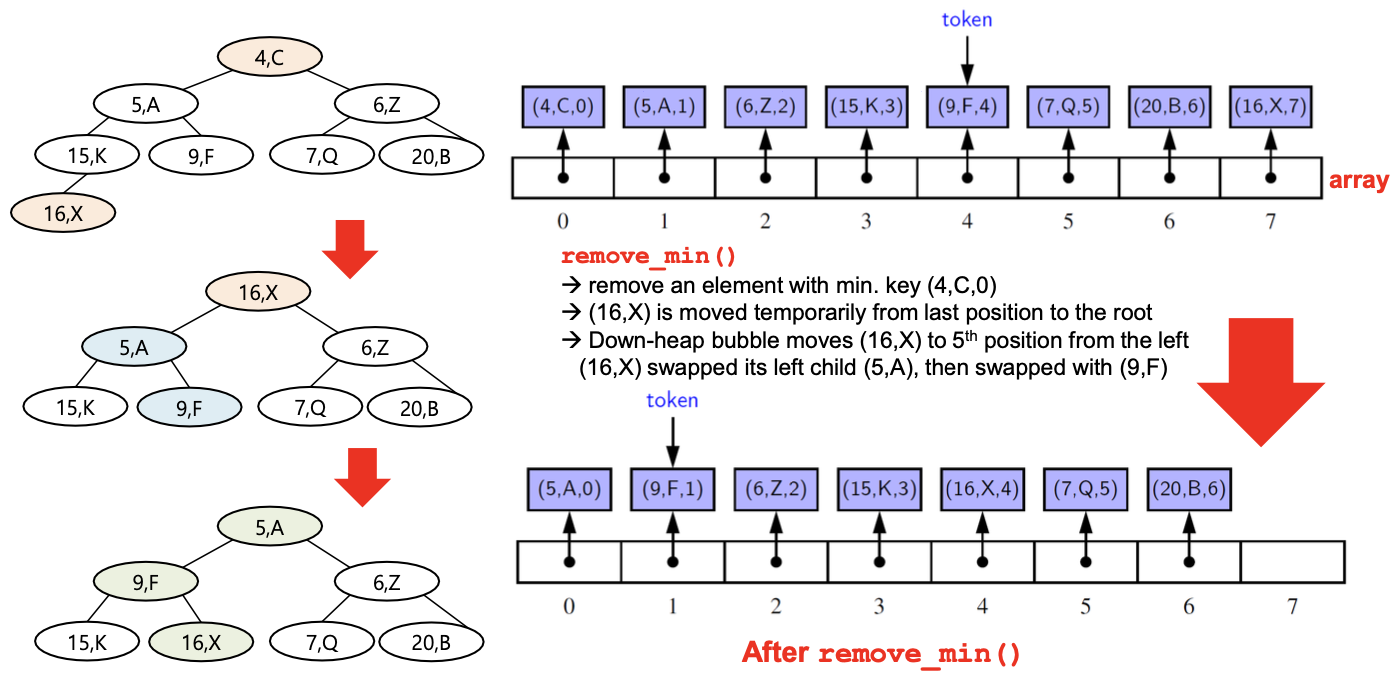
Priority Queue ADT
- Priority Queue : Queue 값들 사이에 우선순위 존재
& minimum key인 요소가 다음에 제거됨 - example
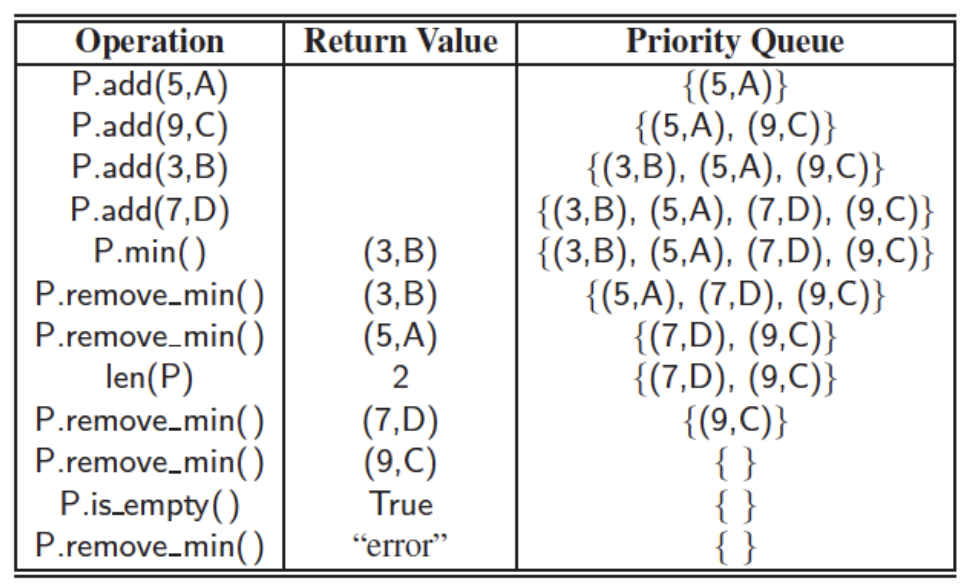
Implementing Priority Queue
- Unsorted List : 삽입 빠르지만 쿼리, 삭제 속도 느림
- 우선순위 높은 O(n) 찾기 (작은 값=높은 우선순위, 높은 값 = 작은 우선순위)
- 우선순위 높은 item Dequeue! O(1)
-> item 삭제된 자리가 비어있어 뒤의 item들을 한칸씩 앞으로 shift
- Sorted List : 쿼리, 삭제는 빠르지만 삽입 느림
- 우선순위로 정렬되어 있어 item삭제는 O(1), 삭제된 부분 메꾸기는 O(n)
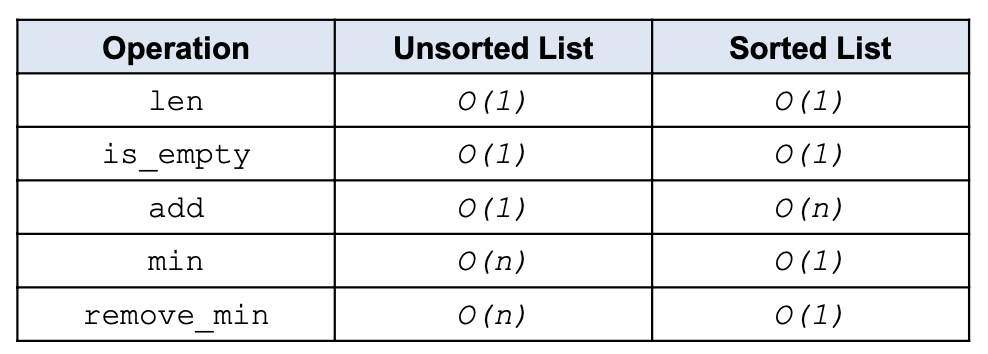
Heaps
: Heap은 binary tree [모양, 순서 조건을 만족]
- Complete Binary Tree (어떤 node가 자식 node를 하나만 가지면 그 노드는 left child에만 존재)
- Heap Order
- Max Heap : parent node 값은 child보다 크거나 같아야 함
- Min Heap : parent node 값은 child보다 작거나 같아야 함
- Implementing Priority Queue with Heap
: Priority Queue 저장하기엔 제일 자연스러운 방식 & 트리 높이 h = [O(nlogn)]
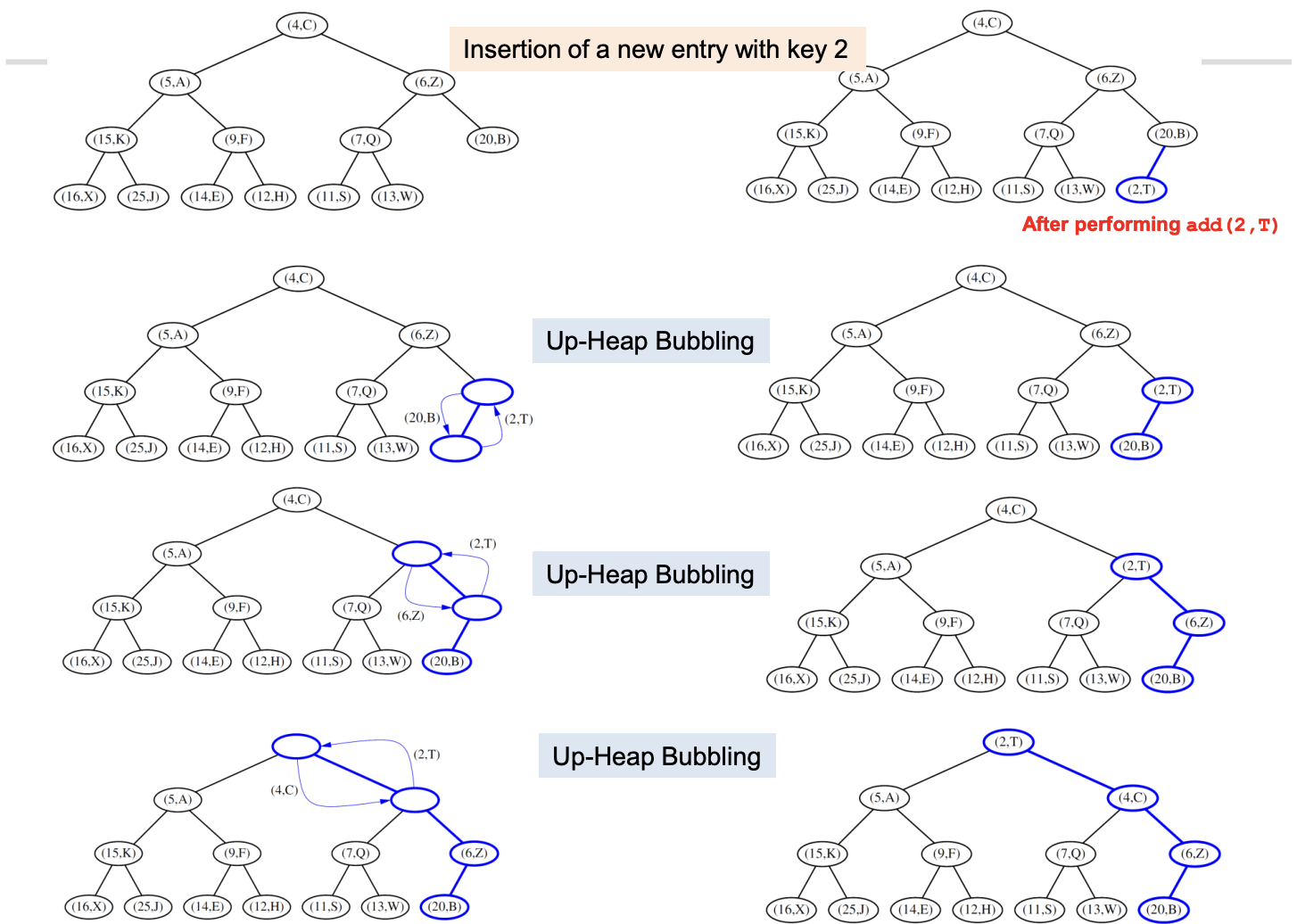
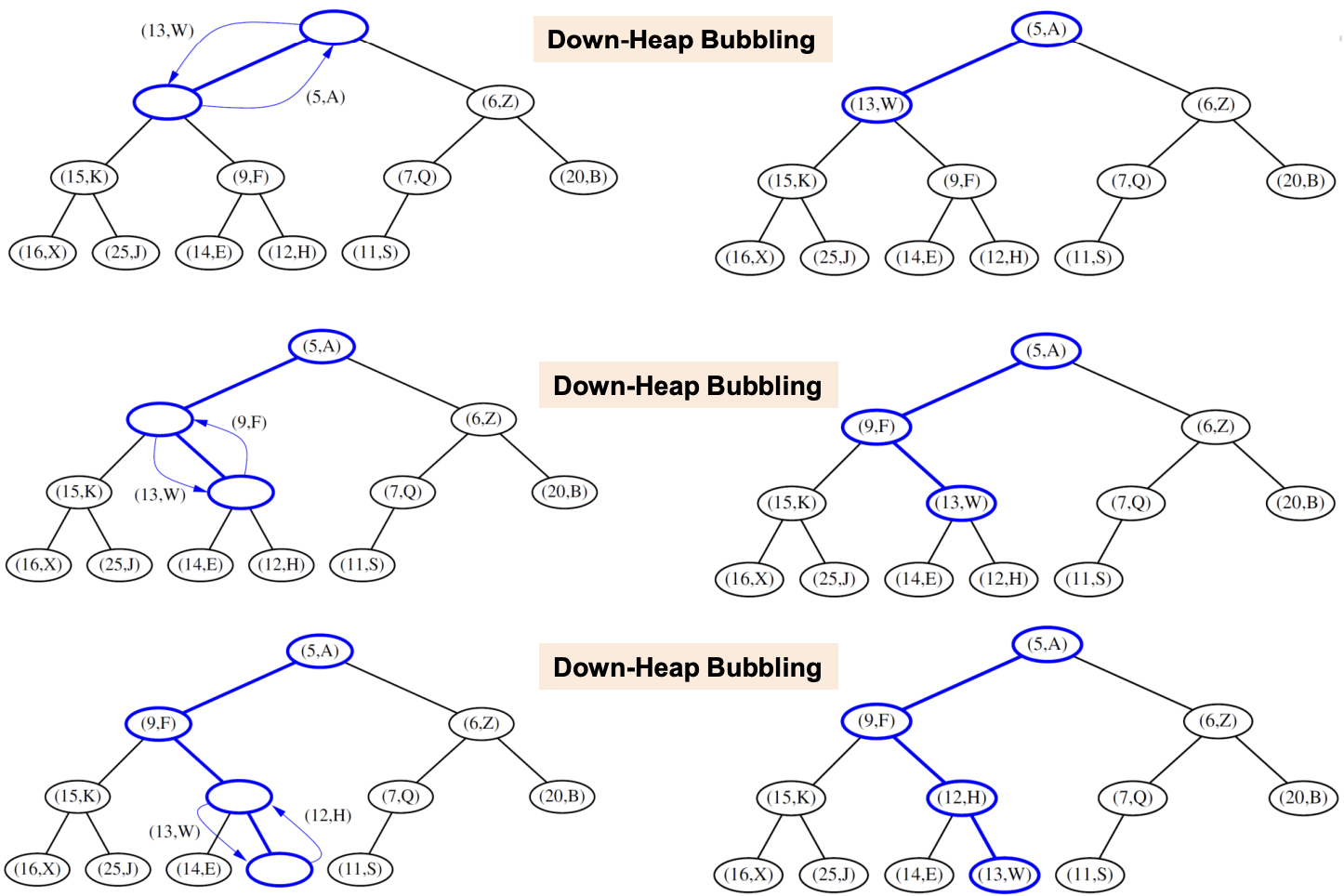
- Bubbling
- up heap bubbling : Min Heap일 경우, 추가된 last node의 entry키가 parent보다 작을때까지 swap 진행
- down heap bubbling : Min Heap일 경우, 변경된 root node의 entry키가 parent보다 클때까지 swap 진행
- Array-based Representation of Complete Binary Tree
: 트리를 array에 저장- p가 root T면, f(p)=0
- p가 position q의 left child면 f(p)=2f(q)+1
- p가 position q의 right child면 f(p)=2f(p)+2
- T의 원소는 범위 [0, n-1]에 있음,

- Analysis of Heap-Based Queue
- Heap 기반 구현 통해 insertion, removal 시 실행시간 단축
- Python's heapq Module
- heappush(L,e) : e를 리스트 L에 push, heap order 복구
- heappop(L) : L에서 최소값을 pop & return하고 heap order 복구
- heappushpop(L,e) : e를 L에 push, 최소값을 pop & return
- heapreplace(L,e) : heappushpop과 비슷함
- heapify(L) : 순서없는 list를 heap-order property로 변형
- nlargest(k, iterable) : 주어진 iterable에서 k개의 최댓값 목록 생성
- nsmallest(k, iterable) : k개의 최소값 목록 생성
Sorting with Priority Queue
-
Selection-Sort
- 기존 priority queue에 있던 값들을 새로운 sequence에 원래 순서대로 옮김
- sequence에서 removeMin을 전체 값의 개수 n만큼 반복, 이 값들을 순서대로 기존 sequence에 옮김
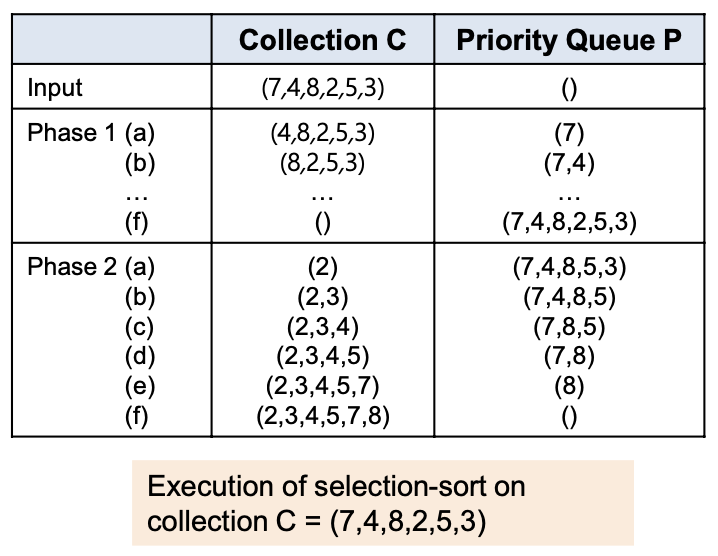
-
Insertion-Sort
- 기존 priority queue에 있던 값들을 새로운 sequence로 옮김(새로운 수가 들어올때마다 우선순위대로 해당 위치에 저장)
- sequence에 존재하는 값들을 순서대로 기존 sequence에 옮김
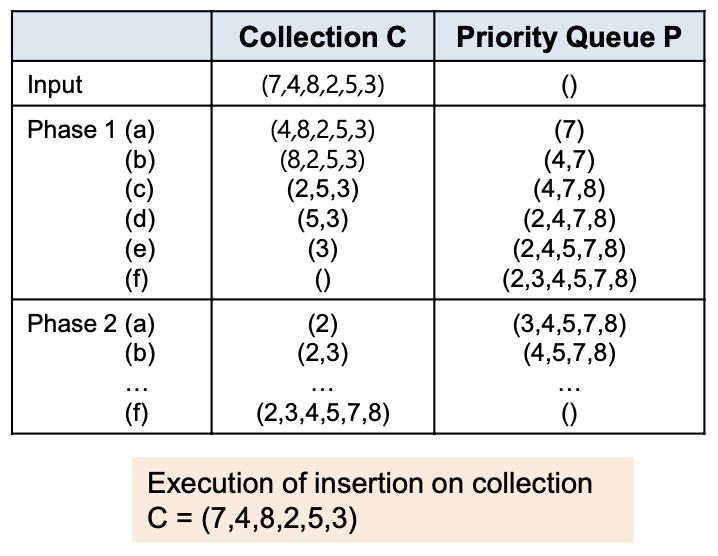
-
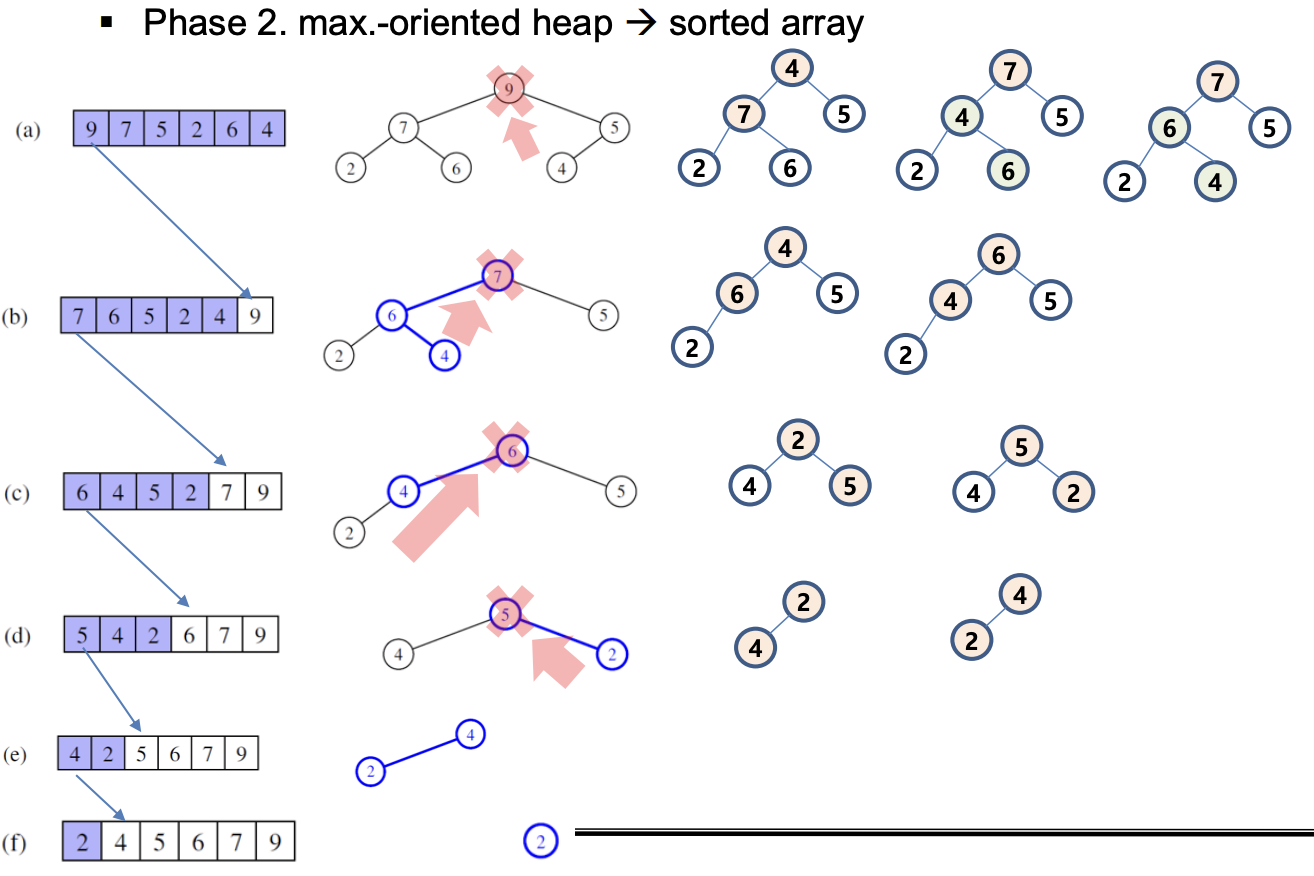
Heap-Sort
- 소요 메모리 양은 O(n)
- insert, removeMin()은 O(logn)의 시간 소요
- size, empty, min은 O(1)의 시간 소요
ex1)
 ex2)
ex2)
Adaptable Priority Queues