스택(Stack)

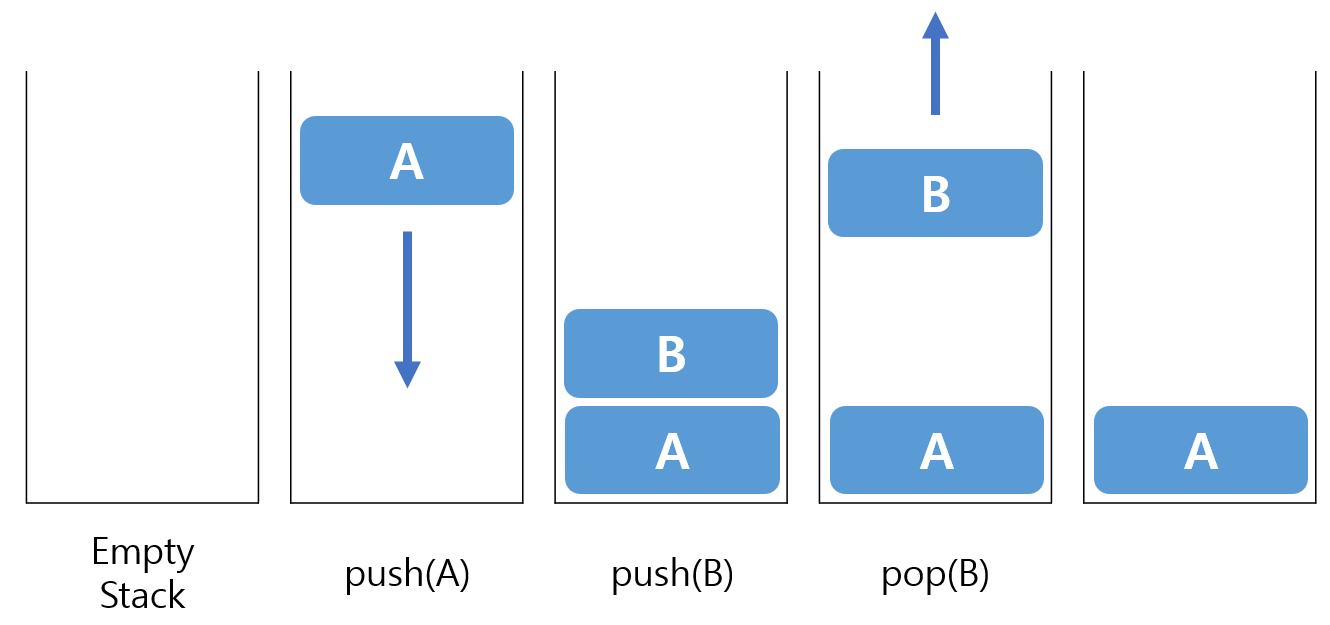
스택은 자료(data element)를 보관할 수 있는 선형 구조 중 하나이다. 위의 그림처럼 넣을 때에는 한쪽 끝에서 밀어넣어야 하고 꺼낼 때에는 같은 쪽에서 뽑아 꺼내야하는 구조로 후입선출(LIFO : Last In First Out) 구조라고도 부른다.

스택이 가질 수 있는 연산

1. size() : 스택에 들어있는 데이터 원소의 수
2. isEmpty() : 스택이 비어있으면 true, 아니면 false 반환
3. push() : 스택에 데이터를 쌓는다.
4. pop() : 스택 가장 위에 있는 데이터를 제거하면서 그 값을 반환한다.
5. peek() : 가장 위에 있는 데이터를 반환한다.(제거 X)

이런 스택을 구현하기 위해서 우리가 배운 배열과 연결 리스트를 사용할 수 있다. 구현하기 전에 5가지 연산 중에서 고려해야 할 사항에 대해 먼저 알아보자.

1. 비어있는 스택에서 데이터 원소를 꺼내려고 한다면 Error!
   -> stack underflow
2. 꽉찬 스택에서 데이터 원소를 넣으려고 한다면 Error!
   -> stack overflow

원래의 스택이라면 크기가 정해져 있어야하지만 우리는 python의 list와 양방향 연결 리스트를 사용하여 구현하기 때문에 크기를 정해놓지 않은 상황으로 구현한다.

스택 구현

stack을 구현하는 것은 양방향 연결 리스트와 내장 자료형인 list를 사용한다면 복잡하지 않게 구현이 가능하다.

선형 배열로 구현

선형 배열은 python의 내장 자료형인 list로 구현한다.

class ArrayStack:
	def __init__(self):
		self.data = []

	# 데이터 원소의 수
	def size(self):
		return len(self.data)

	# 스택이 비어있는가
	def isEmpty(self):
		return self.size() == 0

	# 원소 삽입
	def push(self, item):
		self.data.append(item)

	# 원소 제거 및 반환
	def pop(self):
		return self.data.pop()

	# 맨 위의 원소 확인
	def peek(self):
		return self.data[-1]

연산	시간 복잡도
size()	$O(1)$
isEmpty()	$O(1)$
push()	$O(1)$
pop()	$O(1)$
peek()	$O(1)$

연결 리스트로 구현

양방향 연결 리스트를 사용하여 구현한다.

from doublyLinkedList import Node
from doublyLinkedList import DoublyLinkedList

class LinkedListStack:
	def __init__(self):
		self.data = DoublyLinkedList()

    # 데이터 원소의 수
	def size(self):
		return self.data.getLength()

    # 스택이 비어있는가
	def isEmpty(self):
		return self.size() == 0

    # 원소 삽입
	def push(self, item):
		node = Node(item)
		self.data.insertAt(self.size() + 1, node)

    # 원소 제거 및 반환
	def pop(self):
		return self.data.popAt(self.size())

    # 맨 위의 원소 확인
	def peek(self):
		return self.data.getAt(self.size()).data

연산	시간 복잡도
size()	$O(1)$
isEmpty()	$O(1)$
push()	$O(n)$
pop()	$O(n)$
peek()	$O(n)$

이렇게 직접 구현하지 않고도 python 라이브러리를 이용하여 간단하게 Stack을 사용할 수 있다.
가지고 있는 연산도 동일하며, items라는 메소드가 추가된다. s.items는 현재 스택이 담고 있는 데이터를 list 형태로 보여준다.

from pythonds.basic.stack import Stack

S = Stack()

스택 활용 - 후위 표현식

스택은 후위 표현식을 구현할 때 활용할 수 있다. 우선 후위 표현식이 무엇인지에 대해서 먼저 생각해보자.

중위 표현식 vs 후위 표현식

중위 표기법(infix notation)이란, 사칙연산 혹은 수학식을 표기할 때 현재 우리가 일상적으로 사용하는 방법이다. 연산자가 피연산자들의 사이에 위치한다.

후위 표기법(postfix natation)은 연산자가 피연산자들의 뒤에 위치하는 표기법이다. 후위 표현식은 소괄호, 중괄호, 대괄호를 쓰지 않는다.

중위 표현식	후위 표현식
$(A+B)*(C+D)$	$AB+CD+*$
$A*B+C$	$ABC*+$

중위 표현식 -> 후위 표현식

중위 표현식을 후위 표현식으로 표현하는 방법에 대해서 먼저 알아보자.

1. 중위 표현식의 앞부터 끝까지 차례대로 순서를 갖는다.
2. 피연산자를 만나면 바로 표현식에 쓴다.
3. 연산자는 스택에 넣고 보관한다.
   • 이미 연산자가 있을 때, 만약 스택에 있는 연산자가 현재 연산자보다 우선순위가 높다면 pop하여 표현식에 표기하고 현재 연산자는 스택에 넣는다.
   • 반대로 현재 연산자가 우선순위가 높거나 같다면 스택에 넣는다.
4. 여는 괄호를 만난다면 스택에 push하고 2~3 행위를 반복하다가 닫는 괄호를 만났을 때 스택에 있는 연산자들을 여는 괄호까지 pop한다.
5. 끝까지 모두 2~3의 행위가 끝났을 때 스택에 연산자가 남아있다면 스택이 빌 때까지 pop을 해준다.

말로만 하기에는 이해하기에 어려우므로 그림으로 생각해보자.

예시 1. $A * B + C$ => $AB*C+$

1. $A$ : A를 표현식에 적는다.
   => $A$
2. $*$ : 처음 나온 연산자는 push한다.
   => $A$
3. $B$ : 피연산자인 B를 표현식에 적는다.
   => $AB$
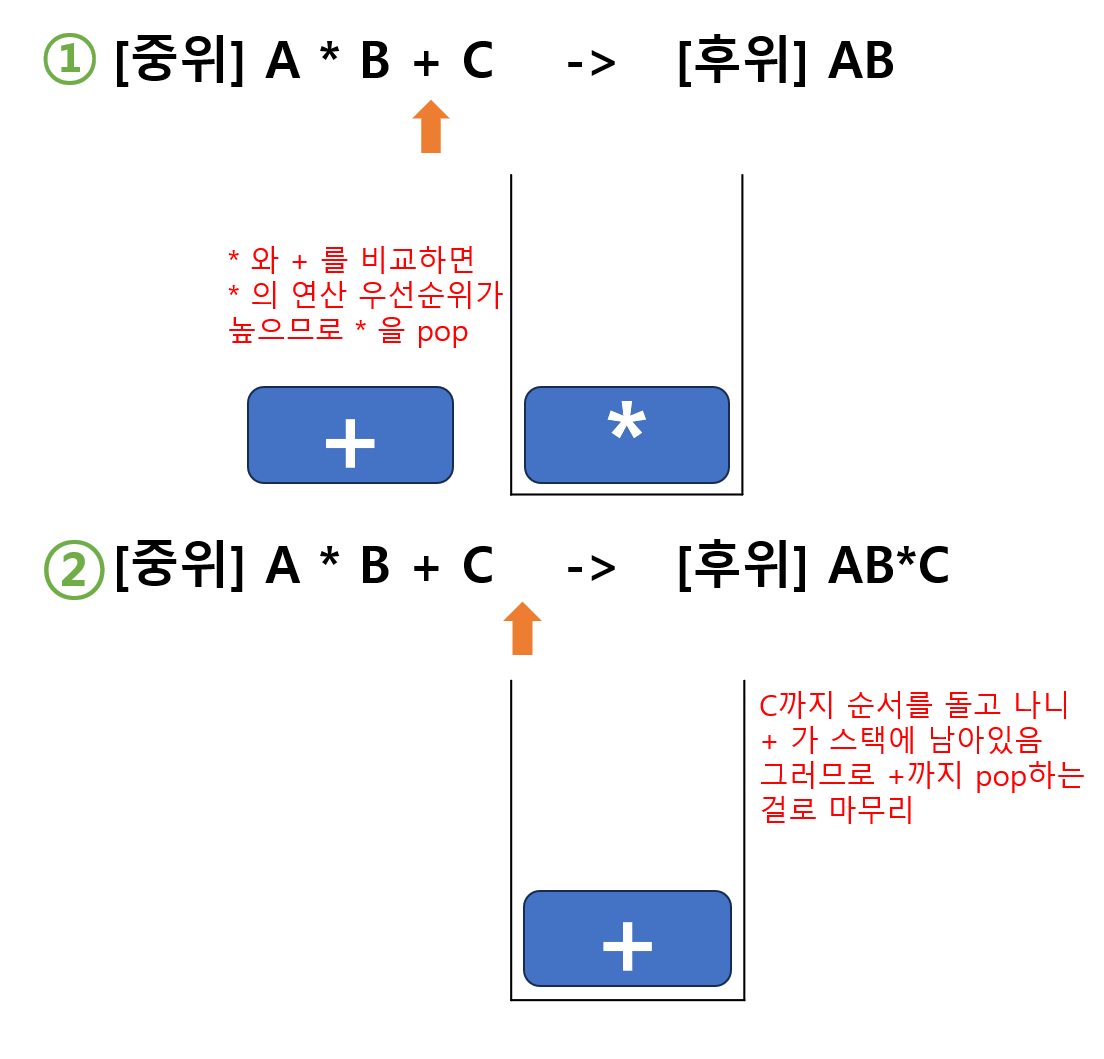
4. $+$ : 그림 1. 스택안에 $*$가 있으므로 $+$와 비교하면 $*$가 우선순위가 높으므로 $*$를 pop을 하고 $+$를 push한다.
   => $AB*$
5. $C$ : 피연산자인 C를 표현식에 적는다.
   => $AB*C$
6. 그림2. 순회가 끝나고 스택에 연산자가 남아있으므로 차례로 pop하여 꺼내면 모든 순서가 끝난다.
   => $AB*C+$

예시 2. $(A+B)*(C+D)$ => $AB+CD+*$

1. $($ : 여는 괄호는 무조건 push
2. $A$ : 피연산자인 A를 표현식에 적는다.
   => $A$
3. $+$ : 스택에는 연산자가 없으므로 push
   => $A$
4. $B$ : 피연산자인 B를 표현식에 적는다.
   => $AB$
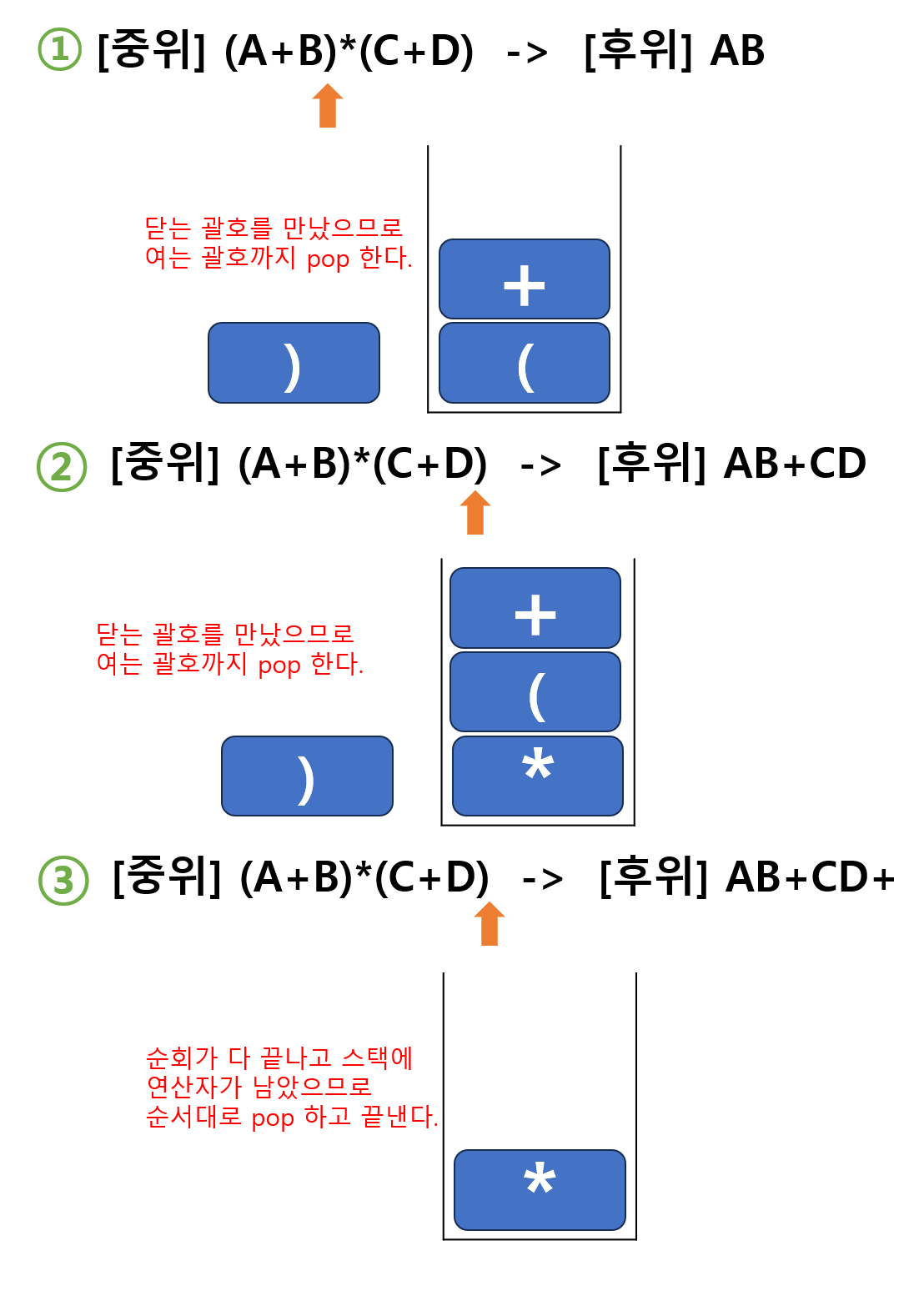
5. $)$ : 그림1. 닫는 괄호를 만났으므로 여는 괄호까지 pop
   => $AB+$
6. $*$ : 스택에 연산자가 없으므로 push
   => $AB+$
7. $($ : 여는 괄호는 무조건 push
   => $AB+$
8. $C$ : 피연산자인 C를 표현식에 적는다.
   => $AB+C$
9. $+$ : 스택바로 위에는 $($이어서 연산자가 없으므로 push
   => $AB+C$
10. $D$ : 피연산자인 D를 표현식에 적는다.
    => $AB+CD$
11. $)$ : 그림2. 닫는 괄호를 만났으므로 여는 괄호까지 pop
    => $AB+CD+$
12. 그림3. 순회가 끝나고 스택에 연산자가 남아있으므로 차례로 pop하여 꺼내면 모든 순서가 끝난다.
    => $AB+CD+*$

위의 2가지 예시를 통해 후위 표현식의 연산 방법에 대해 알아보았다. 그럼 스택을 이용하여 중위 표현식을 후위 표현식으로 바꾸는 방법을 직접 구현해보자.

후위 표현식 구현

# 스택
class ArrayStack:
    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]

# 연산자의 우선순위를 구별하기 위해 
# 각 연산자에 숫자를 지정하여 일정하게 관리하도록 한다.
prec = {
    '*': 3, '/': 3,
    '+': 2, '-': 2,
    '(': 1
}

def solution(S):
    opStack = ArrayStack()
    answer = ''
    
    for s in S:
        if s == '(':
            opStack.push(s)
        elif s == ')':
            while opStack.peek() != '(':
                answer += opStack.pop()
            opStack.pop()
        elif s in prec.keys():
            while not opStack.isEmpty() and prec[s] <= prec[opStack.peek()]:
                answer += opStack.pop()
            opStack.push(s)
        else:
            answer += s
        
    while not opStack.isEmpty():
        answer += opStack.pop()
    return answer

후위 표현식 계산하기

중위 표현식을 후위 표현식으로 전환할 뿐만 아니라 후위 표현식으로 작성된 식을 계산하려고 한다. 이 방법은 사실 굉장히 간단하다.

1. 수식을 왼쪽부터 시작해서 오른쪽으로 차례대로 읽는다.
2. 피연산자가 나타나면, 스택에 넣어 둔다.
3. 연산자가 나타나면, 스택에 들어 있는 피연산자를 두 개 꺼내어 연산을 적용하고, 그 결과를 다시 스택에 넣어 둔다.
4. 이 순회가 끝나고 마지막 스택에 있는 값을 꺼낸다.

후위 표현식을 계산하기 위해서는

1. 문자열로 받은 중위 표현식 중에 연산자와 숫자를 구별할 수 있어야하고
2. 순서대로 배열에 담고 있다가
3. 하나씩 꺼내서 계산을 해야한다.

# 스택
class ArrayStack:
    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]

# 문자열로 받은 표현식을 숫자와 연산자를 구분하고 list에 넣는 함수
def splitTokens(exprStr):
    tokens = []
    val = 0
    valProcessing = False
    for c in exprStr:
        if c == ' ':
            continue
        if c in '0123456789':
            val = val * 10 + int(c)
            valProcessing = True
        else:
            if valProcessing:
                tokens.append(val)
                val = 0
            valProcessing = False
            tokens.append(c)
    if valProcessing:
        tokens.append(val)

    return tokens

# 중위 표현식을 후위 표현식으로 바꾸는 함수
def infixToPostfix(tokenList):
    prec = {
        '*': 3,
        '/': 3,
        '+': 2,
        '-': 2,
        '(': 1,
    }

    opStack = ArrayStack()
    postfixList = []
    
    for token in tokenList:
        if type(token) is int:
            postfixList.append(token)
        elif token == '(':
            opStack.push(token)
        elif token == ')':
            while opStack.peek() != '(':
                postfixList.append(opStack.pop())
            opStack.pop() 
        else:
            while (not opStack.isEmpty()) and (prec[token] <= prec[opStack.peek()]):
                postfixList.append(opStack.pop())
            opStack.push(token)
        
    while not opStack.isEmpty():
        postfixList.append(opStack.pop())

    return postfixList

# 후위 표현식 계산 함수
def postfixEval(tokenList):
    valStack = ArrayStack()
    
    for token in tokenList:
        if type(token) is int:
            valStack.push(token)
        elif token == '+':
            num1 = valStack.pop()
            num2 = valStack.pop()
            valStack.push(num2 + num1)
        elif token == '-':
            num1 = valStack.pop()
            num2 = valStack.pop()
            valStack.push(num2 - num1)
        elif token == '*':
            num1 = valStack.pop()
            num2 = valStack.pop()
            valStack.push(num2 * num1)
        elif token == '/':
            num1 = valStack.pop()
            num2 = valStack.pop()
            valStack.push(num2 / num1)
        
    return valStack.pop()

# 앞의 3가지의 함수를 적용한 결과
def solution(expr):
    tokens = splitTokens(expr)
    postfix = infixToPostfix(tokens)
    val = postfixEval(postfix)
    return val