문제 설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
연결할 수 없는 섬은 주어지지 않습니다.
입출력 예
| n | costs | return |
|---|---|---|
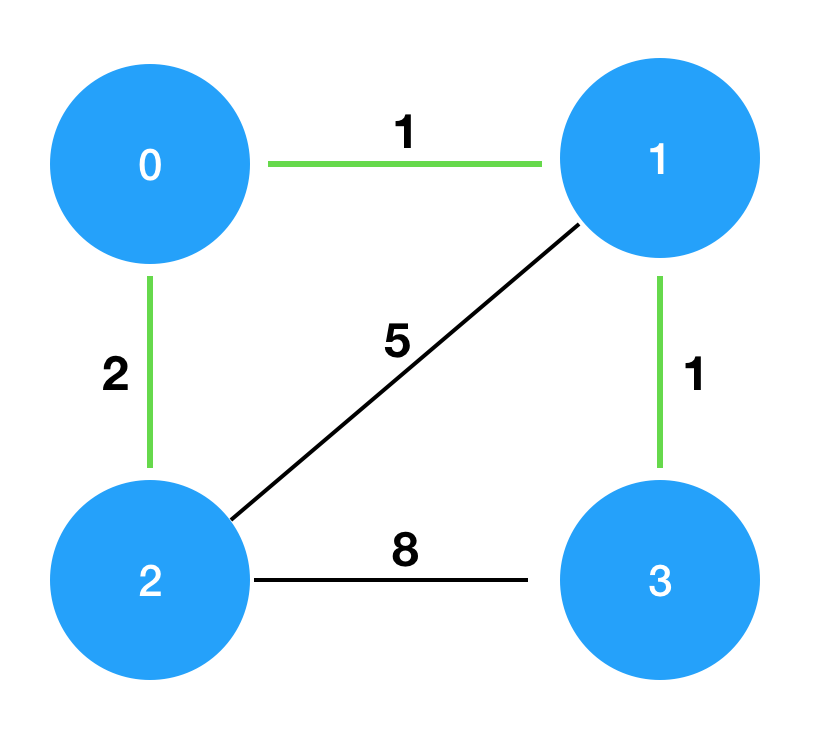
| 4 | [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] | 4 |
입출력 예 설명
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.
풀이
크루스칼 알고리즘을 이용하여 최소 비용 신장 트리를 만들어낸다.
동빈나 쌤의 강의를 참고하여 문제를 해결하였다.
크루스칼의 기본적인 동작 구조는 다음과 같다.
- 적은 비용 기준으로 각 간선들을 정렬한다.
- 정렬된 간선들을 하나씩 꺼내어, 싸이클이 되는 지 검사한 후 총 합에 추가한다.
- 추가된 간선들의 노드들은 다음 사이클 검사를 위해 부모를 일치 시킨다.
- 부모가 모두 같아지면 최소 비용 신장 트리 완성
코드
def solution(n, costs):
answer = 0
costs.sort(key=lambda x: x[2])
cycle = [i for i in range(n)]
# 부모가 일치하지 않을 경우 while 문을 계속 진행
while len(set(cycle)) != 1:
s, e, c = costs.pop(0)
# 서로 부모가 같은 경우는 추가하지 않음
if cycle[s] == cycle[e]:
continue
if cycle[s] < cycle[e]:
# 부모가 같은 다른 노드가 존재할 경우,
# 해당 노드도 부모를 변경 시켜야 한다.
if cycle.count(cycle[e]) > 1:
for i in range(n):
if i == e:
continue
if cycle[i] == cycle[e]:
cycle[i] = cycle[s]
cycle[e] = cycle[s]
else:
if cycle.count(cycle[s]) > 1:
for i in range(n):
if i == s:
continue
if cycle[i] == cycle[s]:
cycle[i] = cycle[e]
cycle[s] = cycle[e]
answer += c
return answer