백준 2023 신기한 소수 찾기

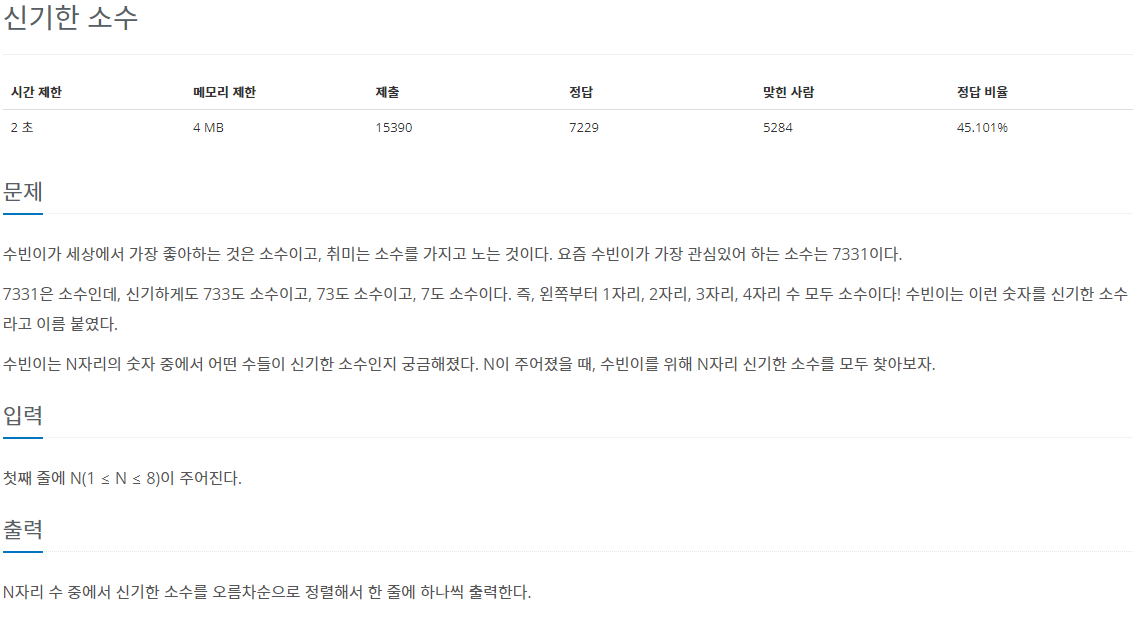
문제

풀이

public class Q2023_신기한소수찾기 {

    static int n;
    static BufferedWriter bw;

    public static void main(String[] args) throws IOException{
        // n 입력 받기
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        bw = new BufferedWriter(new OutputStreamWriter(System.out));
        n = Integer.parseInt(br.readLine());
        // 1.
        dfs(2, 1);
        dfs(3, 1);
        dfs(5, 1);
        dfs(7, 1);
        bw.flush();
        br.close();
        bw.close();
    }

    public static void dfs(int num, int size) throws IOException {
    	// 4.
        if (size == n) {
            if (sosu(num)){
                bw.write(num + "\n");
            }
        }
        for (int i = 1; i <= 9; i++) {
        	// 2.
            if (i % 2 == 0) {
                continue;
            }
            // 3.
            if (sosu(num * 10 + i)) {
                dfs(num * 10 + i, size++);
            }
        }
    }
	
    public static boolean sosu(int num) {
        for (int i = 2; i <= num / 2; i++) {
            // 5.
            if (num % i == 0) {
                return false;
            }
        }
        return true;
    }
}

리뷰

1. 일의 자리 숫자 중에 소수는 2,3,5,7 이므로 왼쪽 첫번째 숫자가 이 중 하나일 경우만 탐색
2. 10의 자리 이상부터 일의자리가 짝수일 경우에는 2로 나뉘어져 소수가 아니므로 이 경우에는 다음 반복으로 넘어감
3. 만약 홀수이고, 소수인 경우에 다음 자리수도 소수인지 탐색
4. 현재 숫자의 자리수가 입력받은 자리수(n)와 같고, 소수일 경우에만 출력
5. 현재 수의 절반을 넘는 약수는 없으므로 현재 숫자의 절반까지만 탐색

이 문제는 아이디어를 떠올리는게 어려웠던 것 같다.
예전에는 소수를 찾을때 그냥 1부터 현재 수까지 약수가 존재하는지를 탐색을 했는데, 절반의 숫자까지만 탐색을 하면 됐다ㅜㅜ
또 처음부터 순차적으로 소수를 찾아가는게 아니라 재귀함수를 호출할 때부터 소수인 경우만을 추려서 재귀함수를 호출하는 방법 등을 통해 수행 시간을 줄이는 방법도 최대한 떠올리려 노력해봐야겠다.