백준 9663 N-Queen

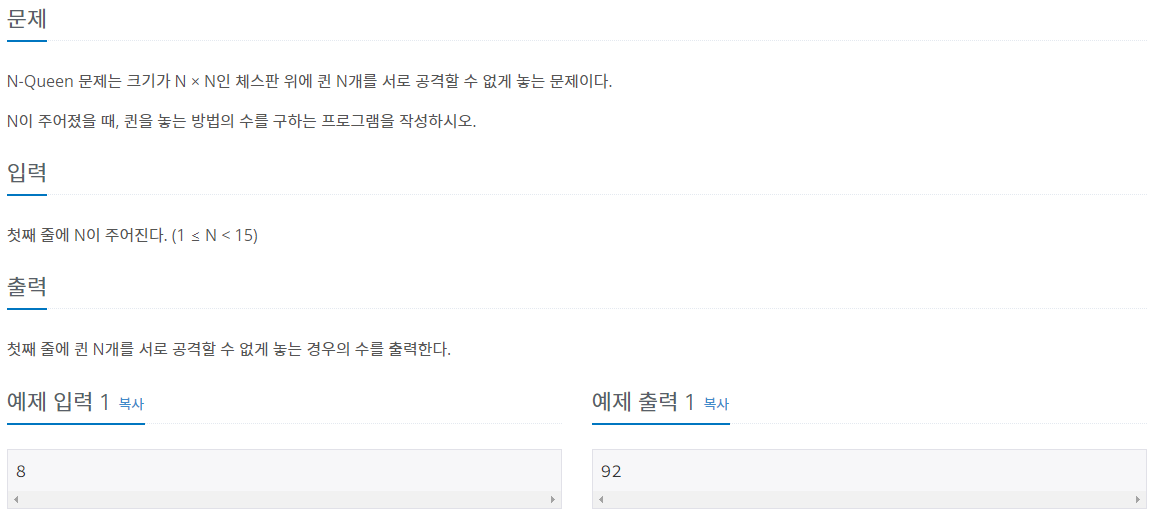
문제

---

리뷰

알고리즘 풀기 시작한지 5일 밖에 되지 않은 평범한 알린이가 풀법한 문제가 아니었다ㅜㅜ
완전탐색으로 분류되어 있었는데 풀이를 확인해보니 dfs라고 보는게 맞을거 같다
처음에는 반복문으로 풀어야하나 싶었다.
그런데 그렇게 하자니 머리에 그려지지 않았다.
결국 인터넷 풀이를 보고도 한참을 이해하지 못해 2시간 넘게 붙들고 있었다.

풀이

체스판은 2차 배열이지만 한 열에 퀸은 하나만 올 수 있으므로 1차원 배열로 대체가 가능하다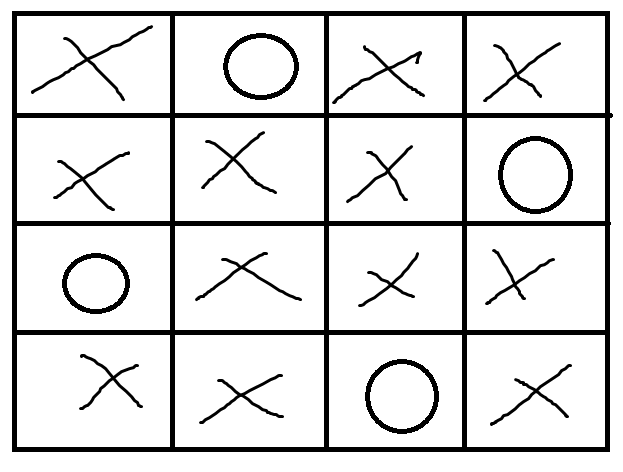

• 위와 같이 퀸이 놓여있다고 하자,
  그럼 각 열을 배열(arr)의 index라고 생각하고 행을 arr[index]의 값이라고 하면,
  배열 arr에는 [2,0,3,1]순으로 값이 들어있을 것이다.
• 퀸은 자신의 상하좌우, 대각선 어디든지 일직선 상에 막혀있는게 없는 한 끝까지 이동이 가능하다
• 이 문제에서 구현해야 할건
• 첫번째로 모든 경우의 수를 구하기 위해 어떻게 재귀함수를 구현할 것인지.
• 두번째로 현재 열, 현재 행에 퀸을 놓을 수 있는지 확인하는 것이다.
• 그걸 구현한 코드는 아래와 같다.
  

public class Q9663 {
    //N-Queen
	
    // 체스판을 나타낼 배열
    static int[] arr;
    // 체스판의 크기와 퀸의 개수를 나타낼 변수
    static int n;
    // n개의 퀸을 체스판에 놓을 수 있는 경우의수
    static int count = 0;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        
        arr = new int[n];
		
        // 재귀함수 시작
        nqueen(0);
        System.out.println(count);

    }
	
    // col은 현재 재귀함수의 열의 위치를 나타냄
    private static void nqueen(int col) {
    	// 배열이라 0부터 시작하는 col의 값이 체스판의 크기 n과 같다는 말은
        // 마지막 열인 col=3에 퀸을 놓는데 성공하여 nqueen(3+1)을 호출했다는 말이므로
        // count를 +1 시켜준다.
        if (col == n){
            count++;
            return;
        }
        for (int i = 0; i<n; i++){
            arr[col] = i;
            // 퀸을 놓을 수 있는 장소인지 확인하는 메서드
            if (able(col)){
                nqueen(col+1);
            }
        }
    }
	
    // 퀸을 놓을 수 있는 장소인지 확인하는 메서드
    private static boolean able(int col) {
    	// 현재 열 위치가 2라고 한다면 0,1번째 열의 퀸 위치도 확인해야 하므로 
        for (int i = 0; i < col; i++){
        	// arr[] 내부의 값(value)들은 행을 나타낸다고 했으므로
            // 서로의 값이 일치한다는건 같은 행에 위치한다는 뜻이므로 false 반환
            if (arr[col] == arr[i]){
                return false;
            // 대각선은 현재 열 - 이전 열과 현재 행 - 이전 행이 같을 때이므로 
            } else if (Math.abs(col-i)==Math.abs(arr[col]-arr[i])) {
                return false;
            }
        }
        // 위의 두 경우가 아니라면 다른 퀸으로부터 안전하다는 뜻이므로 true 반환
        return true;
    }
}

• 전체적인 흐름은 다음과 같다

1. 처음 함수를 호출할 때 인자 값으로 0(첫번째 열)이 들어오면,
2. 먼저 현재 열, 현재 행의 위치가 퀸을 놓을 수 있는 장소인지 확인하고 가능하다면,
3. 그 다음 재귀함수로는 인자값으로 1(두번째 열)이 들어온다.
4. 다시 현재 열, 현재 행에 퀸을 놓을 수 있는지 확인하고 가능하다면,
5. 그 다음 재귀함수의 인자값으로 2(세번째 열)이 들어온다.
6. 이 과정을 마지막 열까지 반복한다

dfs

• 왜 이게 dfs가 아닌가 생각했냐면
• 첫번째 열에서 첫번째 행에 퀸을 놓았을 때, 두번째 열에 퀸을 놓을 수 있는 모든 경우의 수, 세번째 열에서 퀸을 놓을 수 있는 모든 경우의 수, 네번째 열에서 퀸을 놓을 수 있는 모든 경우의 수를 다 찾고 나서야
• 다시 첫번째 열로 돌아와 첫번째 열, 두번째 행에 퀸을 놓았을 때의 경우의 수를 구하게 되기 때문이다.

백트래킹

• 백트래킹도 여기서 처음 봤는데

  백트래킹(Backtracking)은 가능한 모든 경우의 수를 탐색하면서, 어떤 조건을 만족하지 않는 경우에는 더 이상 탐색을 진행하지 않고, 이전 상태로 돌아가서 다른 경우를 탐색하는 알고리즘 기법이다.

• 이 문제에서는 각 재귀함수에서 퀸을 놓을 수 있을지 없을지 확인할 때
• 같은 행인 경우와 대각선에 위치한 경우 false를 리턴함으로서 백트래킹을 구현하였다.

내가 이런 문제들을 과연 풀어낼 수 있을까...?