프로그래머스 당구 연습 - 자바

문제

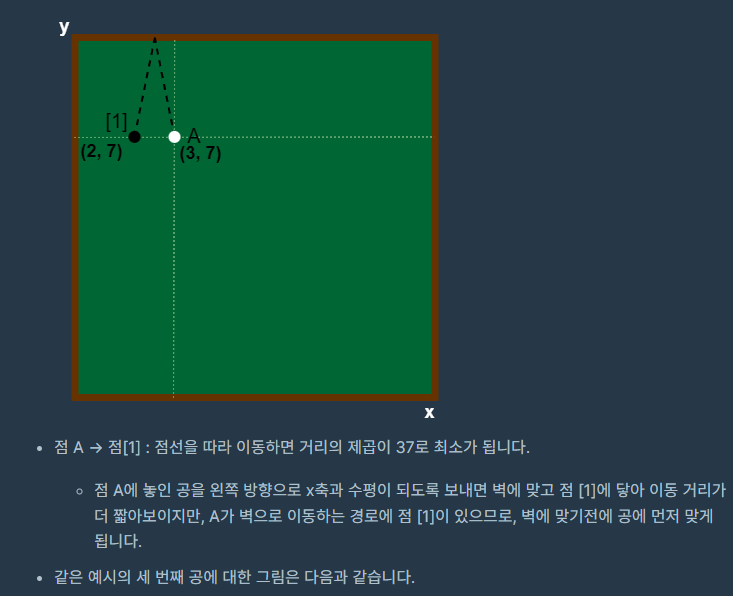
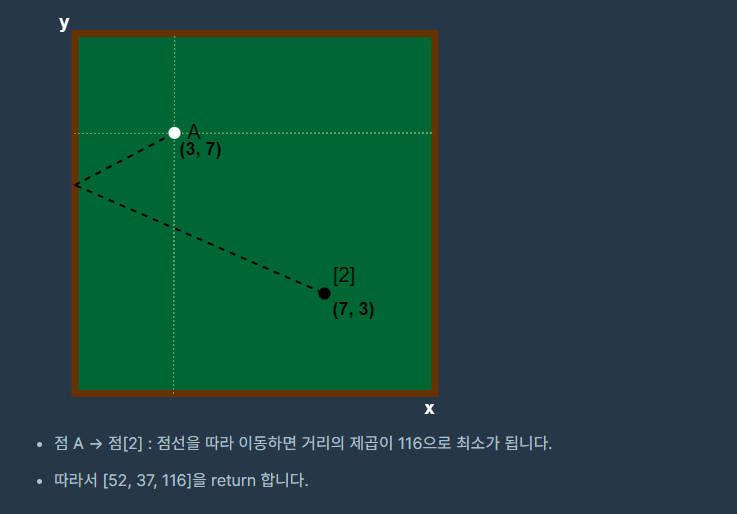
풀이

public class Pro_당구연습 {
    public int[] solution(int m, int n, int startX, int startY, int[][] balls) {
        int[] answer = new int[balls.length];

        for (int i = 0; i < balls.length; i++) {
            int targetX = balls[i][0];
            int targetY = balls[i][1];

            int now = 0; 
            int result = Integer.MAX_VALUE;

            // 원 쿠션이므로
            // x축의 경우
            // 시작 지점에서부터 0 또는 m까지 이동 거리 + 0 또는 m에서부터 타겟까지의 거리를 제곱해야 하고
            // y축의 경우
            // 시작 지점에서부터 0 또는 n까지 이동 거리 + 0 또는 n에서부터 타겟까지의 거리를 제곱해야 함


            // 좌측으로 이동할 경우
            // x축의 0에서 startX까지의 거리
            // x축의 0에서 targetX까지의 거리
            // 이 두가지 거리를 더해서 제곱을 해줘야 함
            if (!(startY == targetY && startX >= targetX)) {
                now = distance(startX, startY, targetX * (-1), targetY);
                result = Math.min(now, result);
            }

            // 우측으로 이동할 경우
            // startX에서 m까지의 거리
            // m에서 targetX까지의 거리
            // 이 두가지 거리를 더해서 제곱을 해줘야 함
            if (!(startY == targetY && startX <= targetX)) {
                now = distance(startX, startY, m + (m - targetX), targetY);
                result = Math.min(now, result);
            }

            // 상
            if (!(startX == targetX && startY <= targetY)) {
                now = distance(startX, startY, targetX, n + (n - targetY));
                result = Math.min(now, result);
            }

            // 하
            if (!(startX == targetX && startY >= targetY)) {
                now = distance(startX, startY, targetX, targetY * (-1));
                result = Math.min(now, result);
            }

            answer[i] = result;
        }

        return answer;
    }

    // 거리를 구하는 공식
    // Math.sqrt(Math.pow((maxX - minX)) + Math.pow((maxY - minY)))
    // 여기서는 거리에 제곱을 한다 했으므로
    // Math.pow((maxX - minX)) + Math.pow((maxY - minY))
    public int distance(int sx, int sy, int tx, int ty) {
        return (int) (Math.pow(sx - tx, 2) + Math.pow(sy - ty, 2));
    }
}

리뷰

두 점 사이의 거리를 구하는 공식에 더해 응용이 필요한 문제였다.
애초에 두 점 사이의 거리를 구하는 공식을 모르면 풀 수가 없는 문제였다.

• 두 점 사이의 거리
  
  그런데 이 문제에서는 거리에 제곱을 한다고 했으므로 루트만 무시하면 된다.

이에 더해 약간의 응용이 필요한데, 그 이유는 원쿠션이라는 조건 때문이다.
시작 지점에서 벽으로의 이동,
벽에서 도착 지점까지의 이동
이 개의 거리값을 총 이동거리로 잡고 두 점 사이의 거리를 구해야한다.

1. 좌측으로 쿠션을 튕길 때

distance(startX, startY, targetX * (-1), targetY);

여기서 타겟에 -1을 곱해주는 이유는 거리를 구하는 아래의 로직에서 두 거리값을 빼는게 아니라 더해줘야하기 때문이다.

public int distance(int sx, int sy, int tx, int ty) {
        return (int) (Math.pow(sx - tx, 2) + Math.pow(sy - ty, 2));
    }

처음에는 이 부분이 잘 이해가 안됐는데, 당구대를 좌표로 생각해야 한다. 아래의 예시를 보자.

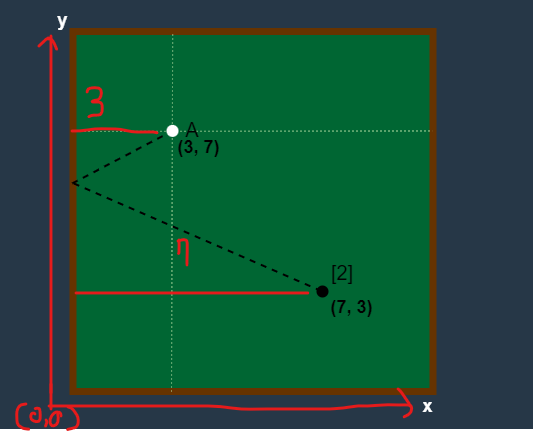
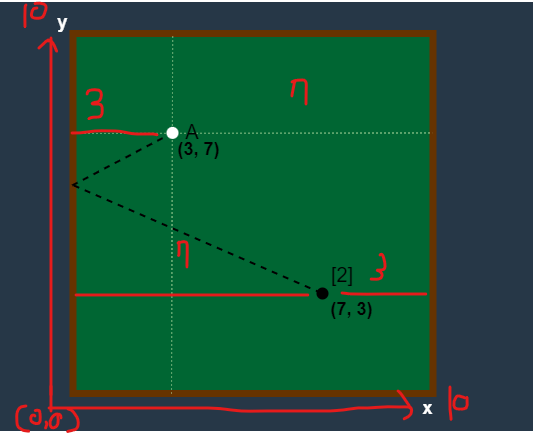
그냥 출발점을 0으로 잡으면 x축 기준 3+7의 제곱으로 100,
y축 기준으로 (7-3)의 제곱으로 16으로 총 거리는 116이 된다.

2. 우측으로 쿠션을 튕길 때,

	distance(startX, startY, m + (m - targetX), targetY);

	public int distance(int sx, int sy, int tx, int ty) {
        return (int) (Math.pow(sx - tx, 2) + Math.pow(sy - ty, 2));
    }

위의 연산에 실제 값을 대입해보면 아래와 같다.
x축을 기준으로,
(3 - 10 + (10 - 7))**2 = 100이 되는데,
3 - 10 = 7 은 시작지점부터 벽까지의 거리
10 - 7 = 3 은 벽에서부터 타겟까지의 거리
y축 기준으로 (7-3)의 제곱으로 16으로 총 거리는 좌측 쿠션과 마찬가지로 116이 된다.

상측 쿠션과 하측 쿠션도 마찬가지이다.