프로그래머스 미로 탈출

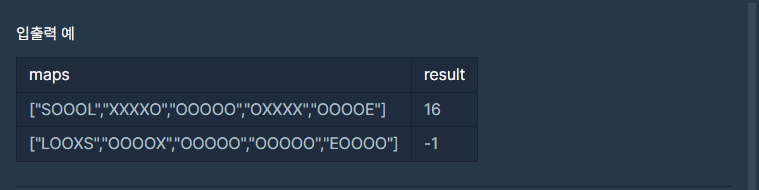
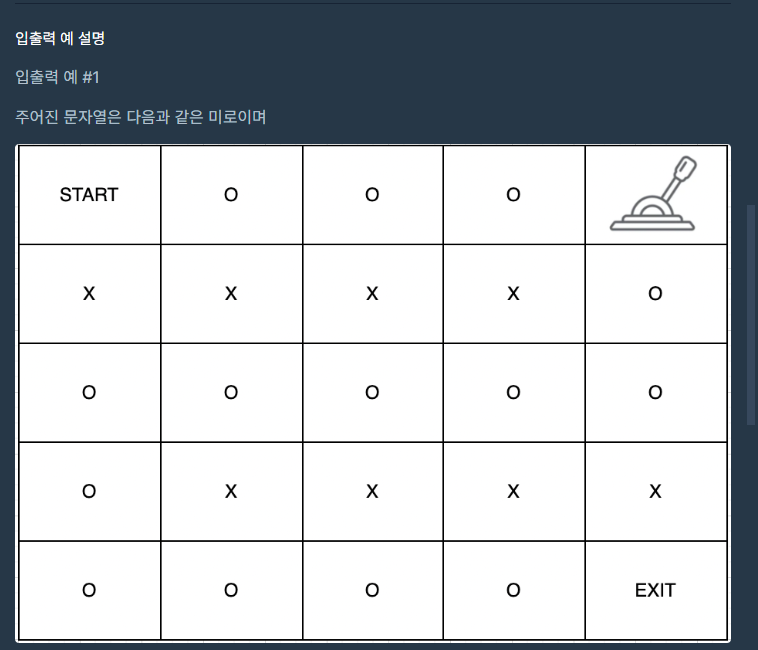
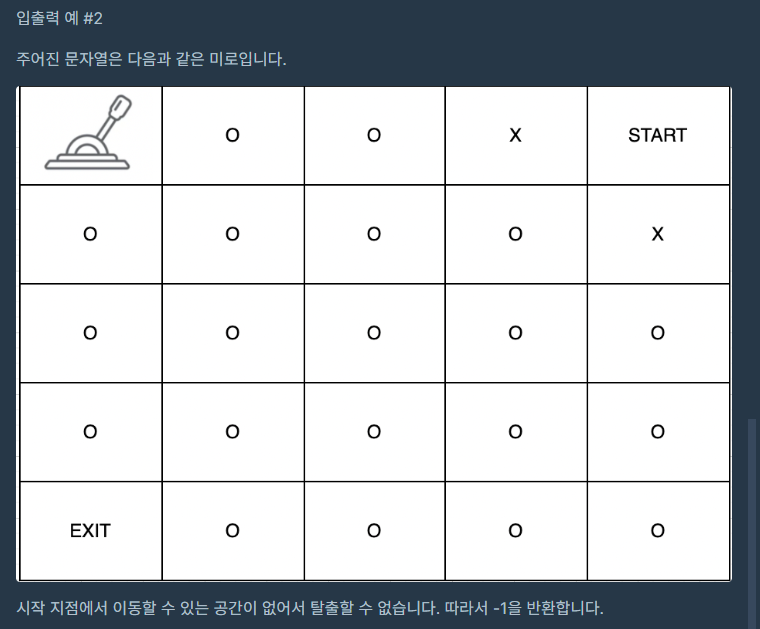
문제

리뷰

처음 보는 유형의 문제라 일단 혼자 해법을 생각해봤다.
현재 위치에서 상하좌우에 있는 칸이 벽이 아니거나 인덱스 값 내에 있는 칸이어야 하는데,
한 칸 움직일 때마다 if문을 적용하고 반복문을 활용하기에는 
현재 칸에서 다음 칸으로 이동할 수 있는 경우의 수가 중첩되어 너무 많아진다. 
거기다가 각 경우의 수마다 소요된 시간을 저장하는 변수를 어떻게 처리할 것인지도 문제였다.
결국 인터넷의 힘을 빌리기로 했다.

해법

이 문제는 큐를 이용해 BFS(넓이 우선 탐색)을 적용하면 풀 수 있다.
BFS는 DFS와는 다르게 현재 노드부터 형체 노드를 먼저 탐색을 하고,
그 이후에 자식 노드와 그 형제 노드를 탐색하는 방식이다.
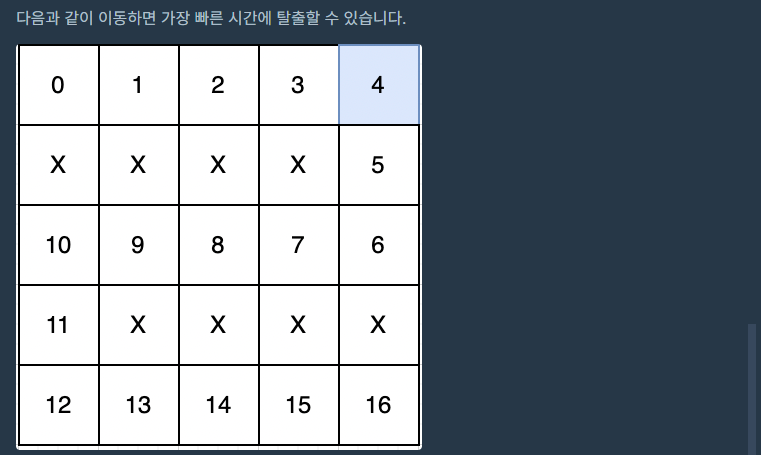
현재 레벨에서 형제 노드를 먼저 모두 탐색하는 방식이기 때문에,
처음으로 목적지에 도착하는 경우의 수가 가장 빨리 도착하는 경우의 수가 된다.
이 문제는 목적지가 2개인데, 레버가 있는 칸, 목적지 칸을 모두 방문해야한다.
때문에 레버칸까지 bfs 한번, 목적지칸까지 bfs 한번 총 두번의 bfs를 수행하면 된다.

코드

import java.util.*;

// 각 칸들의 x,y좌표, 깊이를 저장할 클래스
class Position{
    int x;
    int y;
    int level;
    Position(int x, int y, int level){
        this.x = x;
        this.y = y;
        this.level = level;
    }
}

class Solution {
    
    // 최단 경로를 찾기 위해 한번 방문했던 칸인지 확인하는 배열
    static boolean visited[][];
    // 칸의 정보를 가지고 있는 maps를 2차원 배열로 바꾸기 위한 배열
    static char[][] map;
    
    다음 위치로 이동하기 위해 현재 위치를 저장하는 변수에 더 해줄 값들
    static int[] dx = {-1,0,1,0};
    static int[] dy = {0,-1,0,1};
    
    
    
    public int solution(String[] maps) {
        int answer = 0;
        
        
        visited = new boolean[maps.length][maps[0].length()];
        map = new char[maps.length][maps[0].length()];
        
        // 시작지점을 저장할 변수
        Position startPos = null;
        
        // 중간(레버)지점을 저장할 변수
        Position endPos = null;
        // 끝 지점을 저장할 변수
        Position leverPos = null;
        
        for(int i = 0; i < maps.length; i++){
            for(int y = 0; y < maps[i].length(); y++){
                char single = maps[i].charAt(y);
                if(single == 'S'){
                    startPos = new Position(i,y,0);
                }else if(single == 'E'){
                    endPos = new Position(i,y,0);
                }else if(single == 'L'){
                    leverPos = new Position(i,y,0);
                }
                map[i][y] = single;
            }
        }
        
        // 레버칸까지 걸리는 최소 시간을 측정
        answer = bfs(startPos.x, startPos.y, leverPos.x, leverPos.y);
        
        if(answer > -1){
        	// 레버칸까지 필요한 칸과 끝칸까지 필요한 칸이 겹칠 수도 있으므로 방문 기록 초기화
            visited = new boolean[map.length][map[0].length];
   			
            // 레버칸부터 끝칸까지 걸리는 최소 시간 측정
            int tmp = bfs(leverPos.x, leverPos.y, endPos.x, endPos.y);
            
            if(tmp == -1){
                answer = -1;
            }else{
                answer += tmp;
            }
            
        }
        
        return answer;
    }
    
    public int bfs(int startX, int startY, int endX, int endY){
        Queue<Position> q = new LinkedList<>();
        // 인자로 넘어온 시작 노드의 x,y좌표를 이용해 객체 생성
        q.add(new Position(startX, startY, 0));
        // 칸 하나를 방문한 것이므로 현재 칸을 true로 초기화
        visited[startX][startY] = true;
        
        // q가 비었다는 말은 탐색을 모두 마쳤다는 뜻이므로 그 전까지는 반복
        while(!q.isEmpty()){
        	//처음 들어간 순서대로 하나씩 꺼냄
            Position cur = q.poll();
            int level = cur.level;
            
            //현재 노드의 xy값이 끝 노드의 xy와 일치하면 현재 레벨을 반환
            if(cur.x == endX && cur.y == endY){
                return level;
            }
            
            // 현재 위치에서 상하좌우에 이동할 수 있는 칸이 있는지 확인하기 위한 반복문
            for(int i = 0; i<dx.length; i++){
                int nextX = cur.x+dx[i];
                int nextY = cur.y+dy[i];
                
                // xy가 0보다 작아지거나 배열의 길이 이상이면 반복문을 넘김
                if(nextX < 0 || nextX >= map.length || nextY < 0 || nextY >= map[0].length){
                    continue;
                }
                // 다음 칸을 방문하지 않았고, 다음 칸이 벽이 아니라면
                if(!visited[nextX][nextY] && map[nextX][nextY] != 'X'){
                	// 다음 칸의 좌표와 레벨+1을 q에 저장하고 
                    q.add(new Position(nextX, nextY, level + 1));
                    // 다음 칸의 위치를 저장했다는 말은 다음 칸을 방문한다는 것이므로 true로 초기화
                    visited[nextX][nextY] = true;
                }
            }
            
        }
        // while문이 끝날 때까지 return이 되지 않았다는 것은 목적지까지 갈 수가 없다는 것이므로 -1 반환
        return -1;
    }
}